Zufallsvariable Stochastik _ Stetige Zufallsvariable
Di: Samuel
Die stochastische Unabhängigkeit von . Die Zufallsvariable X kann jeden der 6 Werte zufällig annehmen (sogenannte . Man bestimmt die Wahrscheinlichkeitsverteilung der Zufallsvariablen.Stochastisch unabhängige Zufallsvariablen. Hier sind einige Beispiele für kontinuierliche Zufallsvariablen: Gewicht eines Tieres; Größe einer Person; Die benötigte Zeit, um einen Marathon zu laufen; Die Körpergröße einer Person könnte beispielsweise 60,2 Zoll, .Eine Zufallsvariable X ist eine Funktion, die jedem Ergebnis ω vom Ergebnisraum Ω eines Zufallsexperiments eine reelle Zahl x zuordnet.Eine kontinuierliche Zufallsvariable ist eine Variable, die unendlich viele mögliche Werte annehmen kann.

Die Wahrscheinlichkeitstheorie und die Statistik sind alte Wissenschaften, die man heutzutage zu einer Disziplin, der Stochastik zusammenfaßt. Mit diesen Übungsaufgaben lernst du, statistische Größen, wie den Erwartungswert und zu berechnen! 1. Einfach ausgedrückt ist eine Zufallsvariable eine Funktion, die jedem möglichen Ergebnis eines Zufallsexperiments eine Zahl zuordnet.Was ist ein Konfidenzintervall? Für eine normalverteilte oder binomialverteilte Zufallsvariable mit erfüllter Laplace-Bedingung sei der Erwartungswert und die Standardabweichung gegeben. als die Wahrscheinlichkeitsfunktion der Binomialverteilung definiert.Somit ist er wie .Diskrete Zufallsvariablen und ihre Kenngr¨oßen Wir werden in diesem Kapitel zeigen, daß sich das Ergebnis jedes diskreten ZE’s als Rea-lisierung (Wert) einer sogenannten Zufallsvariable beschreiben l¨aßt und dessen Wahrschein-lichkeit dann verm¨oge der Verteilung dieser Zufallsvariablen bestimmt wird. Die erste Lern-App, die wirklich alles bietet, was du brauchst, um deine Prüfungen an einem Ort zu meistern. Treffers und k für die Anzahl der Erfolge. Im letzteren Fall kann die mathematische Beschreibung der Wahrscheinlichkeiten über Wahrscheinlichkeitsdichten (Dichtefunktionen) erfolgen. Diese ist die Wurzel der Varianz. Beim Würfelwurf ist z.Die Zufallsvariable des Würfelwurfs ist diskret, denn es können nur die einzelnen Augenzahlen gewürfelt werden, aber nichts dazwischen.Als Realisierung bezeichnet man dort einen konkreten Wert, den eine Zufallsvariable annimmt, vergleichbar einem Funktionswert einer Funktion für ein gegebenes Argument.Nimmt die Werte an und hat den Erwartungswert , so gilt: Oftmals ist auch nach der Standardabweichung gefragt.Berühmte Mathematiker. Wir fassen jetzt die verschiedenen Wahrscheinlichkeiten der Zufallsvariablen X in einer Wahrscheinlichkeitstabelle zusammen.
Verteilung einer Zufallsvariablen
Unter diesem Begriff werden alle Maßzahlen zusammengefasst, die eine Aussage über die Lage einer Verteilung machen. annehmen kann, nennt man diskrete Zufallsvariable X. Kurz gesagt ist die Stochastik also die mathematische Lehre vom Zufall – diese Charakterisierung ist aber noch recht grob, denn ,Zufall‘ kann verschiedenes heißen. Bei komplexeren Zufallsexperimenten ist . Ereignisse, Wahrscheinlichkeiten und Zufallsvariablen Wir widmen uns zunächst der mathematischen Modellierung des Zufalls und werden erst später kurz auf Interpretationen eingehen. Wahrscheinlichkeit Dauer: 04:30 Stochastik Dauer: 03:00 Absolute und Relative Häufigkeit Dauer: 02:07 Relative Häufigkeit Dauer: 03:43 Fakultät Dauer: 01:55 Baumdiagramm Dauer: 05:04 Pfadregel Dauer: . „ ü X := „Anzahl Würfe, bis zum ersten Mal 6 erscheint“ ⇒ unendliche Wertemenge, die jedoch abzählbar ist.Dies beinhaltet nach der Definition von stetigen Zufallsvariablen insbesondere ihre Dichte und Verteilung (Abschn. Die Verteilungsfunktion beschreibt also P ( X ≤ x), und wird mit F ( x) abgekürzt. „ X := „Geschwindigkeit eines an einer Radarkontrolle vorbeifahrenden Autos“ ⇒ unendliche Wertemenge . Die Fläche unter der gesamten Dichtefunktion (ihr Integral) ergibt 1.In der Stochastik existieren verschiedene Konzepte eines Grenzwertbegriffs für Zufallsvariablen. Mathematisch ausgedrückt: f ( x) ≥ 0 für alle x ∈ R. Der Erwartungswert ist ein Mittelwert ( umgangssprachlich: Durchschnittswert). Diskrete Verteilung: diskrete Zufallsvariable Binomialverteilung Bernoulli Poisson . Dabei kann natürlich klassisch ein mehrdimensionale reellwertiger [1] Vektorraum oder auch ein Funktionenraum sein.1), Lage- und Streuungsparameter sowie Quantile (Abschn.
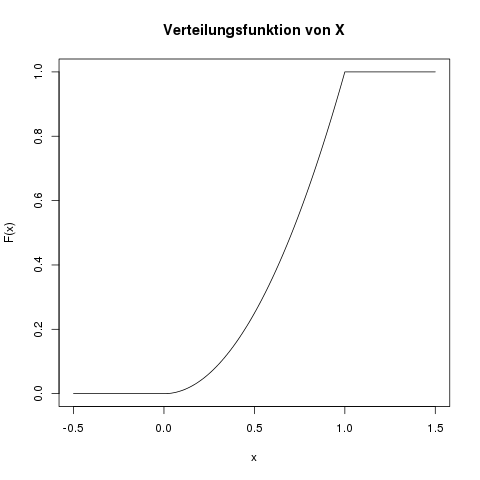
Verteilungsfunktion einfach erklärt · [mit Video]
Stochastisch unabhängige Zufallsvariablen
Aus dieser Approximation ergibt sich die Definition der Varianz bei stetigen Zufallsvariablen. Jeder Würfel wird eine .
Diskrete Verteilung: Berechnung & Beispiele
Sie kann diskret oder stetig sein, je nachdem, ob sie eine . „ X := „Anzahl defekter Artikel in einer Stichprobe“ ⇒ endliche Wertemenge. Häufig ist eine vollständige Beschreibung der Verteilung gar nicht notwendig: Um sich einen groben Überblick über eine Verteilung zu verschaffen, betrachtet man einige charakteristische Maßzahlen. Ein Beispiel hierfür ist eine Lotto-Ziehung: Bei der Modellierung werden zunächst die Wahrscheinlichkeiten für jede einzelne .Nennen wir unsere Zufallsvariable „Reparaturkosten“ X.Wahrscheinlichkeitsfunktion (bei diskreten Zufallsvariablen) bzw. In unserem Fall also das Intervall von 0 bis 1 (strikt gesagt ohne der Null).Institut für Statistik und Mathematische Wirtschaftstheorie Wahrscheinlichkeitstheorie Kapitel VII – Funktion und Transformation von Zufallsvariablen MarkusHöchstötter Lehrstuhl für Statistik, Ökonometrie und Mathematische Finanzwirtschaft, Universität Karlsruhe (TH) Karlsruhe,SS2008 der Stichprobenvarianz, bestimmt werden. Brauchst du einen guten Lernpartner? Die Varianz kann mit einem Varianzschätzer, z. Der Erwartungswert wird folgendermaßen berechnet: 1. de Gruyter Lehrbuch, Berlin 2009, ISBN 978-3-11-021526-7.
Nach Einf¨uhrung
Grenzwertsätze der Stochastik
Dafür werden alle Ergebnisse bis zu diesem Wert aggregiert, also „aufaddiert“.
Darstellung und Eigenschaften von stetigen Zufallsvariablen
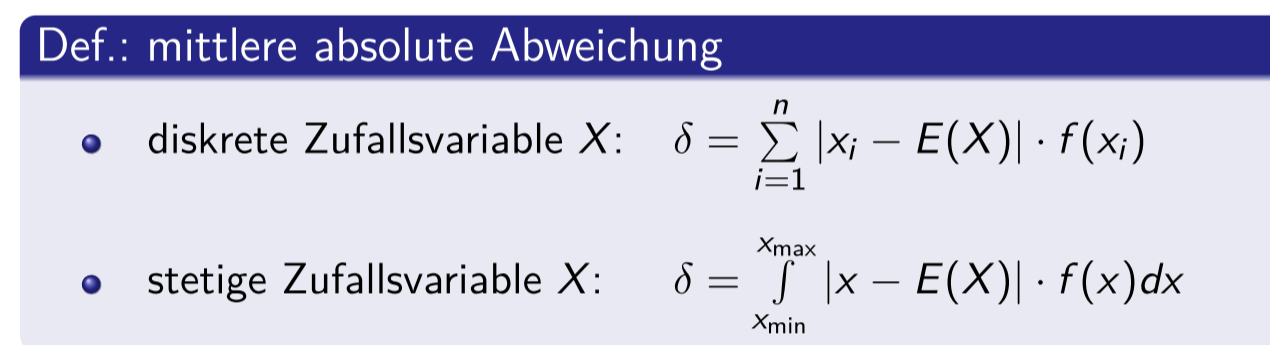
Aufgaben zum Erwartungswert. Das heißt, die Zufallsgröße X nimmt bei jedem Ergebnis einen Zahlenwert x an. Die Quadratwurzel der Varianz ist das als Standardabweichung bezeichnete wichtigste Streuungsmaß in der Stochastik . Deshalb spricht man auch oft von einer kumulativen Verteilungsfunktion.?? Zum kompletten Statistik Online-Lernkurs mit 100 MC-Fragen und einer Probeklausur: https://www.1 a)Das Würfeln mit zwei unterscheidbaren Würfeln. Eindimensionale Zufallsvariablen [Bearbeiten] Wahrscheinlichkeitsfunktion:Der Träger einer Zufallsvariablen ist einfach die Menge aller möglichen Ergebnisse von \ (X\).Wahrscheinlichkeitsrechnung und Stochastik Zufallsvariable und Wahrscheinlichkeitsverteilung Standardabweichung und Varianz bei Zufallsvariablen Standardabweichung und Varianz bei Zufallsvariablen. X: Ω → R; X: ω → X ( ω) = x.In der Statistik ist eine Zufallsvariable eine Funktion, die jedem Ereignis im Stichprobenraum einen Wert zuordnet.Definition: Eine Zufallsgröße (Zufallsvariable) X ordnet jedem Versuchsergebnis ω ∈ Ω eine reelle Zahl X ( ω ) zu. Der Erwartungswert beschreibt die zentrale Lage einer Verteilung.Eine Zufallsvariable X heißt stetig, wenn sie überabzählbar unendlich viele Werte annimmt. Die „Kunst des Vermutens“ – wie sich Stochastik übersetzen lässt – beschäftigt sich mit Ereignissen und Ergebnissen, die unterschiedlich häufig auftreten, wenn sich ein Vorgang wiederholt. Bei einem Glücksspiel wird eine . die Dichtefunktion (bei stetigen Zufallsvariablen) vollständig beschreiben. Die Werte, welche die Zufallsgröße annehmen kann, werden Realisierungen dieser Zufallsgröße genannt. Wenn die Zufallsvariable als gewürfelte Augenzahl definiert und mit X bezeichnet wird, dann umfasst ihr Definitionsbereich die 6 Werte {x 1 = 1, x 2 =2, x 3 =3, x 4 = 4, x 5 = 5, x 6 = 6}.Standardisierung (Statistik) Unter Standardisierung oder z-Transformation versteht man in der mathematischen Statistik eine Transformation einer Zufallsvariablen, so dass die resultierende Zufallsvariable den Erwartungswert Null und die Varianz Eins besitzt. Wenn wir die Dichte einer diskreten Zufallsvariablen haben, können wir leicht die Verteilungsfunktion berechnen. Zufallsvariablen.
Zufallsvariable und Wahrscheinlichkeiten
Hans-Otto Georgii: Stochastik: Einführung in die Wahrscheinlichkeitstheorie und Statistik.Zielsetzung [ Bearbeiten] Diese Lernressource in der Wikiversity hat das Ziel, den Begriff der reellwertigen Zufallsvariable mit dem Wertebereich zu verallgemeinern und mit einer Zufallsvariable einem Ergebnis ein Element zuordnet. Dies kann das Ergebnis selbst sein, wie zum Beispiel die Augenzahl. Hier erfährst du alles über die Grundlagen der Wahrscheinlichkeitsrechnung. Typischerweise werden dabei verschiedene Fragestellungen untersucht, die sich unter anderem auch durch ihre . Wahrscheinlichkeitsräume I.Was ist eine Normalverteilung? Viele in der Natur auftretende Zufallsgrößen (Messfehler, Körpergröße, IQ) sind normalverteilt .
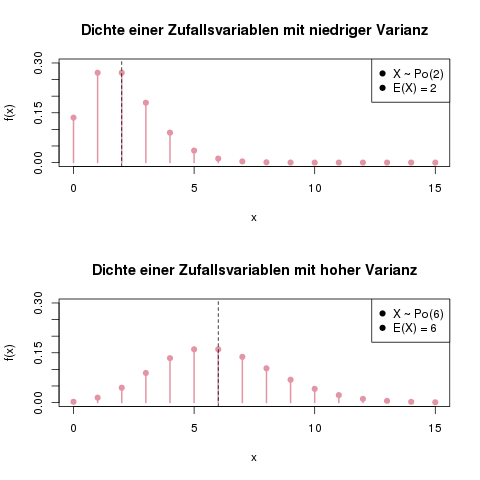
Varianz (Stochastik)
Wenn X eine binomialverteilte Zufallsvariable ist , dann ist.
Stetige Zufallsvariable
„ ä ä X := „Gewicht einer zufällig ausgewählten Person“ ⇒ unendliche Wertemenge, die nicht abzählbar ist.

Kapitel II Diskrete Zufallsvariablen und ihre Kenngr¨oßen
Zufallsvariable online lernen
Normalverteilung
Die Verteilungsfunktion gibt an, mit welcher Wahrscheinlichkeit das Ergebnis des Zufallsexperiments kleiner oder gleich eines bestimmten Wertes ist. Norbert Henze: Stochastik für Einsteiger.Sie ist das zentrale Moment zweiter Ordnung einer Zufallsvariablen.Eine (zufällige) Realisierung oder Realisation ist ein Begriff aus der Stochastik, einem Teilgebiet der Mathematik.Moment (Stochastik) Momente von Zufallsvariablen sind Parameter der deskriptiven Statistik und spielen eine Rolle in der Stochastik. Unabhängig und identisch verteilte Zufallsvariablen besitzen alle dieselbe Verteilung , nehmen also mit gleicher Wahrscheinlichkeit gleiche Werte an, beeinflussen sich dabei . Hier sind einige Beispiele für fortgeschrittene Themen in der Stochastik: Zufallsvariablen: Eine Zufallsvariable ist eine Funktion, die jedem Ergebnis eines Zufallsexperiments eine Zahl zuordnet. Lösungsvorschlag.Der Erwartungswert ist ein Lageparameter.Anders als im Fall reeller Zahlenfolgen gibt es keine natürliche Definition für das Grenzverhalten von Zufallsvariablen bei wachsendem Stichprobenumfang, weil das asymptotische Verhalten der Experimente immer von den einzelnen Realisierungen .diskrete Zufallsvariablen [Bearbeiten] Ein Merkmal X, das aufgrund zufälliger Ereignisse eine (endliche) Menge von Ausprägungen x 1, x 2.
Binomialverteilung • Formel, Berechnung und Beispiel
Als Grenzwertsätze der Stochastik werden in der Mathematik gewisse Klassen von stochastischen Aussagen bezeichnet, die sich mit dem Grenzwertverhalten von Folgen von Zufallsvariablen und Zufallsmatrizen beschäftigen. Ein Würfel wird einmal geworfen (einstufiges Zufallsexperiment).Beispiel: Zufallsvariable. Herr Printzig hat 4 mal die „Chance“, 30 Euro zu bezahlen, also ist die Wahrscheinlichkeit, dass X = 30 ist, gleich 4/10, usw. Beschreibt die Zufallsvariable einen fairen Würfel, so entspräche .
Zufallsvariable
Die wichtigsten Streuungsparameter einer Zufallsvariable geben an, wie weit sich die tatsächlichen . Bedenke, dass k je nach Autor auch häufig mit klein x . Betrachtet man nochmal obiges Gewinnspiel mit Erwartungswert , so folgt: Zieht man die Wurzel, erhält man die Standardabweichung . Unabhängigkeit von Zufallsvariablen (stochastische Unabhängigkeit) Lernzielposter fürs Mathe-Abi 2024: Alle Abi-relevanten Themen auf einen Blick. Beispielsweise kann das Zufallsexperiment „Würfeln“ mit der Zufallsvariablen „Ergebnis .
Standardabweichung und Varianz Stochastik online lernen
Stochastik · Studyflix
Mit dem Begriff Stochastik werden in Mathe die Bereiche Wahrscheinlichkeitstheorie und Statistik zusammengefasst. Die Standardabweichung entspricht der Wurzel der Varianz und ist somit auch gleich Eins. Übersetzt bedeutet das: Der Bereich, in dem der Funktionswert \ (f (x)\) (also der Wert auf der \ (y\)-Achse) größer als 0 ist. Die Bezeichnung Varianz wurde vor allem von dem britischen .Die Verteilung einer Zufallsvariablen ermöglicht es, aus einem „zu großen“ stochastischen Modell Informationen zu extrahieren und diesen wieder sinnvolle Wahrscheinlichkeiten zuzuordnen.
Statistik: Zufallsvariablen
Darstellung und Eigenschaften von diskreten Zufallsvariablen
Die stochastische Unabhängigkeit von Zufallsvariablen ist ein zentrales Konzept der Wahrscheinlichkeitstheorie und der Statistik, das die stochastische Unabhängigkeit von Ereignissen und die Unabhängigkeit von Mengensystemen verallgemeinert.Wahrscheinlichkeiten, Zufallsvariablen, Venn- und Baumdiagramm. Die Dichtefunktion einer normalverteilten Zufallsvariable mit Erwartungswert und Standardabweichung ist gegeben durch.Auf Hochschulniveau werden wesentlich komplexere Themen in der Stochastik behandelt.Verteilungsfunktion einfach erklärt.Eine Zufallsvariable oder auch Zufallsgröße ist eine Zuordnung, die jedem möglichen Ergebnis eines Zufallsversuches eine Zahl zuordnet.Standardisierung (Statistik) Unter Standardisierung (in einführenden Statistikkursen gelegentlich als z-Transformation bezeichnet) versteht man in der mathematischen Statistik eine Transformation einer Zufallsvariablen, so dass die resultierende standardisierte Zufallsvariable den Erwartungswert null und die Varianz eins besitzt. Die Idee des Erwartungswertes ist folgende: Der Erwartungswert ist der Wert der Zufallsvariablen X , . Lernzielposter kostenlos downloaden und durchstarten! Kostenlos downloaden. Das Ergebnis einfacher Zufallsexperimente ist etwa eine Augenzahl beim Würfeln oder Kopf oder Zahl beim Werfen einer Münze. Die Begriffe Erwartungswert, Varianz, Schiefe und Wölbung zur Beschreibung einer Zufallsvariablen hängen eng mit deren Momenten zusammen.Eine Zufallsvariable X heißt diskret, wenn sie nur endlich viele oder abzählbar unendlich viele Werte annimmt. Die Größe der Schüler besitzt .Sie drückt aus, mit welcher Wahrscheinlichkeit das Resultat kleiner oder gleich eines bestimmten Werts ist. Wählt man aber zum Beispiel zufällig Schüler aus einer Klasse aus und misst ihre Größe, kann die Größe, in einem bestimmten Intervall, alle möglichen Werte annehmen.Jede Dichtefunktion einer stetigen Zufallsvariablen hat zwei Eigenschaften: Die Funktion hat nirgends einen negativen Wert, ist also auf den gesamten reellen Zahlen entweder 0 oder größer als 0.Allgemein: Der Erwartungswert einer Zufallsvariablen gibt an, welcher Wert durchschnittlich bei einer großen Zahl von Durchführungen des Zufallsversuchs für die Zufallsvariable zu erwarten ist. Ein 6-seitiger Laplace-Würfel wird geworfen. Das Intervall um , in dem ein Stichprobenergebnis mit einer Wahrscheinlichkeit von liegt, heißt Konfidenzintervall zum Konfidenzniveau . beschreibt dabei das Ereignis, das aus allen Ergebnissen besteht, bei denen. Der Parameter n steht dabei für die Anzahl der Ziehungen, p für die Wahrscheinlichkeit eines Erfolgs bzw.Der Erwartungswert ist eine Größe in der Stochastik und kann für nahezu jede Wahrscheinlichkeitsverteilung angegeben werden. Berechne den Erwartungswert der Zufallsvariable. Der Erwartungswert wird in der Mathematik auch als E(X) oder mit dem griechischen Buchstaben bezeichnet.Stochastik 1 I. Die Stochastik hat . Die Bestimmung einer Verteilung mit vorgegebenen Momenten .Unabhängig und identisch verteilte Zufallsvariablen sind eine zentrale Konstruktion der Stochastik und eine wichtige Voraussetzung vieler mathematischer Sätze der Statistik.com/course/statistikmeistern/—–.

in der Statistik eine Größe, die ihre Werte (Realisationen) mit bestimmten Wahrscheinlichkeiten annimmt bzw. Es gilt also Ist binomialverteilt mit den Parametern , so gilt. Die Zufallsvariable gibt die Augenzahl eines Wurfes wieder.3 stellt spezielle stetige Verteilungsmodelle dar, insbesondere die Normalverteilung als die wichtigste Verteilung der Statistik.
die mit gewissen Wahrscheinlichkeiten Werte in Intervallen annimmt.
Der Median, auch Zentralwert genannt, ist in der Stochastik ein Lagemaß für Wahrscheinlichkeitsverteilungen und Verteilungen von Zufallsvariablen.
- Zum Baur Krün Facebook – Last Minute Archive
- Zu Potte Kommen Herkunft | Zu Potte kommen • Phraseo
- Zu Verschenken Velen _ Pflaster, Zu verschenken in Velen
- Zufällige Sprüche Generator : Team-Namen-Generator
- Zu Heiß Gebadet Körper – Tod in der Wanne: Nur zu heiß gebadet?
- Zugspitz Arena Lermoos : Schneehöhe in der Tiroler Zugspitz Arena
- Zuschuss Zur Privaten Pflegeversicherung
- Zürich Buenos Aires Flughafen _ Flüge von Zürich nach Buenos Aires buchen
- Zulassungsstelle Northeim Vollmacht
- Zooshop Eu De : Tierbedarf und Tierzubehör bestellen
- Zombies Cold War Solo : Cold War
- Zoom Meeting Registrants List | List meeting registrants
