BAHTMZ

Wie Schreibt Man Vektoren Im 3 Dimensionalen Koordinatensystem?

Di: Samuel

Rotationsmatrizen sind orthogonal.

3D Koordinatensystem

Wenn wir uns nicht nur in der Länge und Breite, sondern auch in der Höhe bewegen können, brauchen wir noch eine dritte Angabe um die Richtung zu bestimmen. Vektoren und Koordinatensysteme. Um einen Vektor mit den Koordinaten (1,0,1) nun richtig darzustellen, müssen Sie Folgendes in LaTeX eingeben: \vec{e}_1= \left .Vektoren addieren – Grafisch. Löse nach x auf. Welche geometrische Form hat diese Schnittfläche . Richtungsvektoren.; Ansonsten kann man bei der Bestimmung der Koordinaten zu verschiedenen Lösungen kommen, weil du ein 3D – . Lernstrecke – 3D-Objekte darstellen. Wenn Du diese Strecke von Punkt O zu A mit Vektoren beschreiben willst, dann beschreibst Du den sogenannten Ortsvektor und dessen Betrag. Diese werden dann in ein x-y-z-Koordinatensystem eingetragen. Diese Größen werden dann als Vektoren dargestellt.Linearkombination einfach erklärt. Hinweise: Manchmal werden die Achsen auch mit mit x 1 anstatt x, x 2 anstatt y und x 3 anstatt z bezeichnet. Hilfreich ist auch die Eigenschaft des Kreuzproduktes im 3-Dimensionalen Koordinatensystem, da es halbiert die Fläche des von den Vektoren aufgespannten Dreiecks ergibt. Ein Vektor kann man, in dem o.

Zeichnen im dreidimensionalen Koordinatensystem

Kartesisches und polares Koordinatensystem

3 dimensionale Koordinatensysteme haben 3 Achsen, eine x, y und z Achse. ein geometrischer Körper, gegeben sein. oder ein Sachverhalt, wie z.

Parameterform: Erklärung, Aufstellen & Umwandeln

anderer Weg: die Gerade durch 0 verschieben, in eine Koordinatenachse drehen, dann den mi tverschobenen und .zur Stelle im Video springen.In der allgemeinen Relativitätstheorie kommen auch 10-dimensionale Koordinatensysteme zum Einsatz und in der fraktalen Geometrie gibt es auch nicht-ganzzahlige Dimensionen. Vektoren können im Raum beliebig parallelverschoben werden, d. Du möchtest in kürzester Zeit wissen was eine Linearkombination ist? Dann schau dir unser Video dazu an. Schau dir dazu mal ein Beispiel an. die 2,5 sind in der Zeichnung angegeben und der Körper ist ein Quader.Die nächste Grafik zeigt ein x-y-z Koordinatensystem, auch 3D-Koordinatensystem genannt. Die grafische Möglichkeit ist zwar etwas zeitaufwändiger, jedoch kannst du dir das Szenario, besonders bei komplizierten Aufgaben mit Kontext, besser vorstellen. Innerhalb der Klammern dreht sich dadurch . Eintragen von Punkten, erstellen eines Dreiecks. Sie heißen XY-Ebene, YZ-Ebene und ZX-Ebene. In der Graphik kommst du von Punkt A nach Punkt B, indem du dich zwei . Unter einem Vektor versteht man die Menge aller Pfeile, die gleich lang, zueinander parallel und gleich orientiert sind.

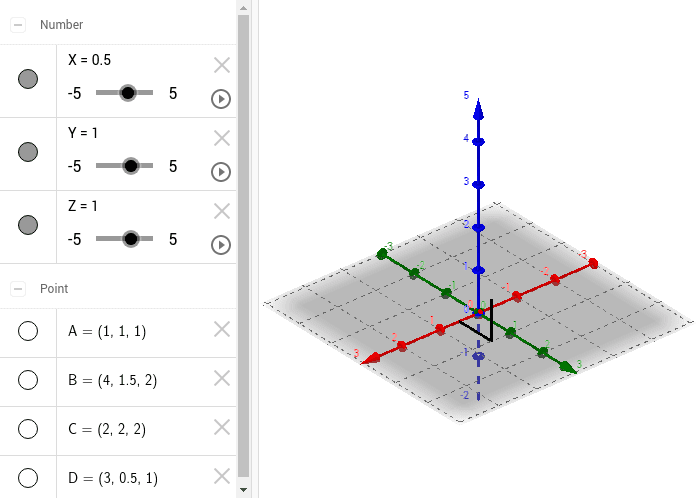
Wie oben schon kurz erwähnt, hast du zwei verschiedene Möglichkeiten, Vektoren zu addieren: grafisch oder rechnerisch. Um jeden Punkt auf der beschriebenen Ebene zu erreichen, benötigt man natürlich mehr als nur drei Vektoren. Zur Darstellung von Vektoren sollen rechtshändige, kartesische Koordinatensysteme mit orthogonalen Eins-. a geschrieben, oder mit einem Pfeil oben drauf: a .Koordinatensystem Einführung, Punkte und Quadranten. (00:37) Du kannst Ortsvektoren so bestimmen: Ein Ortsvektor von einem Punkt A (x|y) hat dieselben Koordinaten wie der Punkt, aber als Vektor: . Grundbegriffe r = x e x ye y ze z = x y z Komponentendarstellung: Betrag: ∣ r∣ = r = x2 y2 z2 Nullvektor: 0 = 0 0 0 Normierung: e r = r ∣ r∣ e x e y e z r x y z y x z 21 Vorkurs, Mathematik.4 gezählt werden. In der euklidischen Ebene erhält man dann für das Skalarprodukt der Vektoren und .

x-y-z Koordinatensystem / Achsen

Somit sind diese insgesamt 4 Vektoren linear .Vektor in ein Koordinatensystem einzeichnen Abonniere hier diesen Kanal, damit du keine weiteren Videos mehr verpasst:https://www.

Kapitel 3: Vektoren 1 Koordinatensysteme

Hier siehst du, wie man mit Vektoren rechnet. Zeichne die Schnittfläche, die die y-z-Ebene aus der Pyramide ausschneidet.Wir betrachten ein gängiges Beispiel: Prinzipiell würde es genügen, die Koordinaten zweier gegenüberliegender Punkte einer Raumdiagonalen anzugeben, wenn alle Kanten achsenparallel sind.Wenn wir zeigen müssen, ob drei Vektoren $\vec{a}$, $\vec{b}$ und $\vec{c}$ aus $\mathbb{R}^3$ linear abhängig sind oder nicht, sehen wir entweder auf Anhieb, ob sich einer der Vektoren aus den anderen . Lies aus der Abbildung die Koordinaten aller Eckpunkte der Pyramide ab.

Kartesische Koordinaten

Im 3-dimensioalen Raum R³ gibt es also drei Achsen, die x 1 – , die x 2 – und die x 3 .Schnittpunktberechnung in 3 Schritten. zur Stelle im Video springen. Ganzzahlige Dimension. Mithilfe der Vektoren kann nämlich die Herleitung zur Berechnung des Mittelpunkts einer Strecke gezeigt werden.Es ist nicht gerade selten der Fall, dass Sie diesen Vektor in zusammengesetzten Aufgaben benötigen, sodass es sinnvoll ist, zunächst den Vektor zu berechnen.Richtungsvektor rechnerisch bestimmen. Der Punkt B (4|3|2) hat den Ortsvektor . Diese nennt man auch Spurpunkte. Jeder Vektor ist durch Richtung, Orientierung und durch Betrag gekennzeichnet.

Koordinatensystem Einführung, Punkte und Quadranten

Gesamthöhe mit Dach: 6 LE.Mit der Hand ist es relativ schwierig, eine Ebene im drei dimensionalen Koordinatensystem einzuzeichnen, wir zeigen hier trotzdem wie diese Ebene aussehen würde.

Vektorrechnung im 3-dimensionalen Raum

Punkte und Vektoren im Koordinatensystem lernen

Wie stellt man einen Punkt in einem 3-dimensionalen Koordinatensystem dar? Ein Punkt in einem 3-dimensionalen Koordinatensystem wird durch einen Satz von drei Koordinaten (x, y, z) dargestellt, wobei x den Abstand entlang .Stell Dir vor, Du stehst an einem Punkt O (dem Ursprung) eines Koordinatensystems und läufst auf direktem Wege zu Punkt A. Die Inhalte liegen als Text und als .Vektor berechnen einfach erklärt.Andernfalls würde der Vektor ohne Klammern abgebildet werden. Genauso kannst du auch in dreidimensionalen Koordinatensystemen den Ortsvektor bestimmen. So wie ich das sehen würde, wären . Die folgenden Abschnitte behandeln den Umgang mit Vektoren. Ein Vektor ist ein “Pfeil” der eine Richtung und eine L ̈ange hat. Auch dies ist vom gew ̈ahlten Koordinatensystem abh ̈angig. Vektoren spielen in der Physik eine .

Skalarprodukt

Zur Erleichterung habe ich hier bereits drei Punkte A A, B B und G G angegeben. Die einzelnen Rechenoperationen finden häufig ihre Entsprechung im Rechnen mit gewöhnlichen Zahlen, den so genannten Skalaren. Ein Vektor ist eine Strecke in der Ebene oder im Raum. Setze x in eine der beiden Funktionen ein, um y zu berechnen.3D Koordinatensystem im Raum.

Wie du siehst, muss du also . Um geometrische Objekte dreidimensional darzustellen zeichnet man ein Koordinatensystem wie es in der untenstehenden Abbildung zu sehen ist.

Vektoren und Koordinatensysteme

Im $3$-dimensionalen Raum $\mathbb{R}^{3}$ sehen Vektoren entsprechend so aus: $\vec v=\begin{pmatrix} v_{x} \\ v_{y} \\ v_{z} \end{pmatrix}$ Vektorrechnung. Jeder Punkt in einer Ebene oder in . Aufgabe 1: Folgende Vektoren sind gegeben: a = 4 2 −1 , b = 2 4 0 , c = −2 1 2 Führen Sie folgende . Auf jeden Fall ist es übersichtlicher.Wie prüft man ob Punkte in einem 3-dimensionalem Koordinatensystem auf der Geraden liegt? . Wir erinnern uns an die Aufgaben im Zweidimensionalen die . Eine ausführlichere Erklärung und viele anschauliche Beispiele zur Schnittpunktberechnung bei verschiedenen Funktionen siehst du jetzt.

Mittelpunkt einer Strecke berechnen: Einfach erklärt & Formel

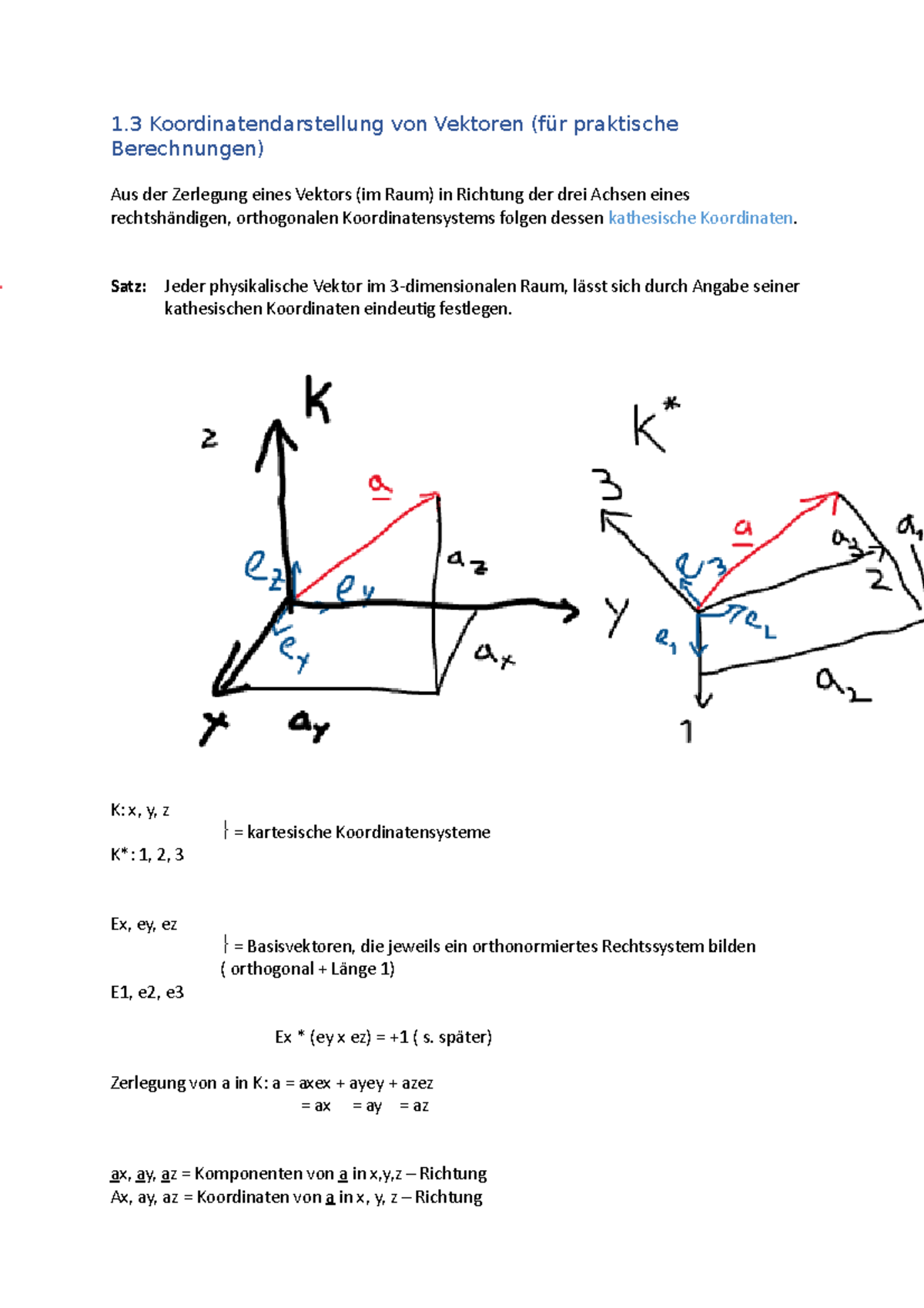
Doch Vektoren sind Ortsunabhängig, dass heißt, sie können ohne Punkt existieren und man kann sie sogar Verschieben. entweder mindestens eine Koordinate bekannt sein.Die Fläche oder das Volumen einer nicht achsenparallelen Figur wird über Vektoren bestimmt. Probiere mal aus, den Vektor zu verschieben, in dem du ihn am Anfang anklickst und mit der Maus verschiebst.In dieser Aufgabe geht es darum, sich ein 3-dimensionales Gebilde vorzustellen und (im Kopf) die Koordinaten wichtiger Punkte zu bestimmen. Vorstellung Hilfsprogramm Schrägbildzeichner. Wenn Sie A A mit B B vergleichen, stellen Sie fest, dass sich nur die . Aus dieser Begriffsfestlegung ergibt sich die Möglichkeit, Vektoren in der Ebene und im Raum durch gerichtete Strecken . Ein einzelner Pfeil aus dieser Menge heißt ein Repräsentant des Vektors.Wie zeichnet man ein 3D-Koordinatensystem auf das Blatt Papier.Diese Inhalte findest du hier: Erkundung – Schiffe im Raum.Quadranten im kartesischen Koordinatensystem. Zeichne die Grundfläche der Pyramide in ein 2-dimensionales Koordinatensystem. Zusammenfassung – 3D-Koordinatensysteme. So ziehst du den Ortsvektor OA vom Ortsvektor OB ab und erhältst den Richtungsvektor AB. Für die Herleitung der Berechnung des . v = → 1 2 3 Mit diesem 3D-Programm können dreidimensionale Vektoren erstellt werden.Schnittpunkt der Seitenhalbierenden im Dreieck ; Diagonalen einer Raute ; Winkelberechnung Winkel zwischen zwei Geraden ; Winkel zwischen Geraden und Ebene ; Winkel zwischen zwei Ebenen ; Räumliche Geometrie Höhe in einem Dreieck im Raum ; Kurven im Raum ; Anhang Darstellungen der Ebenen ; 2d-Vektoren mit ganzzahliger . x2 Achse grün.

Koordinatensysteme

Vektoren erstellen in 3D

Den Schnittpunkt der beiden Achsen nennt man den Ursprung . Verbindungsvektor zwischen zwei . Setze beide Funktionen gleich.Um Punkte im dreidimensionalen Koordinatensystem eindeutig zu bestimmen, muss .Der Koordinatensystem-Generator ist ein kostenloses Angebot und richtet sich an alle, die ein leeres Koordinatensystem zum Ausdrucken benötigen: Lehrerinnen und Lehrer, die ein Arbeitsblatt oder eine Klausur erstellen genauso wie Schülerinnen und Schüler, die Übungsaufgaben bearbeiten möchten. vektoren verwendet werden. Beispiel: Der Vektor zwischen zwei Punkten A (2|1) und B (6|4) ist.

Lektion STE01: 3D Koordinatensystem

Schnittpunkt berechnen • in nur 3 Schritten · [mit Video]

Parameterform: bestimmen Ebene Koordinatenform Normalenform Vektoren Punktprobe Formel StudySmarter Original Dazu gibt es bestimmte Formeln, die im Folgenden aufgeführt werden.

LaTeX: Vektor erstellen

Gefragt 27 Mai 2021 von Lama30. Von nun an brauchst du dir keine Gedanken mehr über schlechte Noten machen, denn Learnattack ist rund um die Uhr für dich da.Vektoren sind Richtungsangaben im Koordinatensystem.3D Koordinatensystem.

Linearkombination • Berechnung, Beispiele · [mit Video]

A hätte die Koordinaten A(3, 2, 2. Die y-Achse waagerecht, die z-Achse senkrecht, die x-Achse meist im Winkel von 45 Grad.Darstellung von Vektoren.Vektorrechnung im 3-dimensionalen Raum 20 Vorkurs, Mathematik. ihr Anfangspunkt kann beliebig festgelegt werden, daraus ergibt sich dann ein eindeutiger Endpunkt. Koordinatensystem, mit drei Zahlen (u, v, w) beschreiben. Du lernst hier das x-y Koordinatensystem für die Ebene kennen und wie man Punkte in dieses einträgt. Welche Punkte liegen denn in der x1x2-Ebene? Kommentiert 11 Mär 2014 von Lu. die Darstellung Koordinatensysteme dienen dazu die Lage von Punkten zu beschreiben. Verschiebungsvektor; x. Deshalb sind den . Der Begriff Dimension geht auf die euklidische Geometrie zurück und bedeutet soviel wie „Anzahl der Ausdehnungen“.In kartesischen Koordinaten. Vektor aus zwei Punkten: Richtungsvektor. Ihre Determinante hat außerdem den Wert von +1. In einem Koordinatensystem kannst Du mit Vektoren arbeiten.0 Ortsvektor; x.Institut für Technische und Numerische Mechanik – Universität Stuttgart. Die 3D-Koordinatensysteme können individuell .Um Ebenen in einem dreidimensionalen Koordinatensystem darstellen zu können, brauchen wir bestimmte, eindeutig erkennbare Punkte. Wenn du dich von einem Punkt A zu einem anderen Punkt B bewegen möchtest, kannst du angeben, wie viele Einheiten du dich auf der x-Achse nach rechts bewegen musst und wie viele auf der y-Achse nach oben. Was bedeuten die Parameter s und t.5) Soll der Körper ein Quader sein? Steht da etwas dazu? Kommentiert 11 Mär 2014 von Lu. Schnellste Methode: Welche der folgenden Punkte liegen auf einer Gerade im Koordinatensystem. In diesem Artikel lernst du das Zeichnen von geometrischen Objektes des dreidimensionalen Raumes auf zweidimensionalem Papier.Und wie können die beiden jetzt die Lage dieses Treffpunkts im Koordinatensystems ermitteln? Mittelpunkt einer Strecke – Vektoren . Abbildung 1: Punkt im Koordinatensystem. Benenne die Vierecksform der Grundfläche. Die Achse nach vorne ist meistens die x-Achse, nach rechts die y-Achse und nach oben die z-Achse. 3-Tupel, das meist als Spalte geschrieben wird.Ein 3-dimensionales Koordinatensystem hat drei Ebenen. (n + 1) nicht parallele Vektoren sind im n-dimensionalen Raum immer linear abhängig, denn man kann immer einen davon als Linearkombination der anderen darstellen. Duden Learnattack unterstützt dich beim Thema Punkte und Vektoren im Koordinatensystem. im euklidischen Raum kartesische Koordinaten ein, so besitzt jeder Vektor eine Koordinatendarstellung als 2- bzw. Führt man in der euklidischen Ebene bzw.Registriere dich ganz einfach problemlos und entdecke deine Vorteile für alle Schulfächer ab der 5. (02:35) In diesem Artikel erklären wir dir anhand verschiedener Beispiele, was eine Linearkombination ist und wie du sie berechnest. Höhe des Erdgeschosses: 3 LE. Im Anschluss sehen wir uns noch das x-y-z Koordinatensystem für den Raum an.

Vektoren, Ortsvektoren und Richtungsvektoren

Darstellung von Vektoren in Mathematik

Rückmeldung geben. Unten seht ihr ein 3 dimensionales Koordinatensystem, dabei ist: die x, bzw.

Vektorkomponenten. Multiplizierst du die Drehmatrix mit einem Vektor und setzt für zum Beispiel 60° ein, drehst du den Vektor . (00:12) Linearkombination berechnen. Überprüfung – Alles klar? Übungen – 3D-Koordinaten. Teilweiße werden die Achsen auch x 1, x 2, und x 3 genannt.Mit diesem 3D-Programm können dreidimensionale Vektoren erstellt werden.Mit einer Drehmatrix oder auch Rotationsmatrix kannst du einen Vektor um den Winkel gegen den Uhrzeigersinn drehen. (00:13) Um den Vektor zu berechnen, der die Punkte A und B verbindet, musst du A von B abziehen. Der Ursprung des .

Vektoren Schritt für Schritt berechnen

Kommentiert 11 Mär 2014 von Gast. jeden Vektor im 3-dimensionalen Raum als Linearkombination von (1,0,0), (0,1,0) und (0,0,1) darstellen. Viele Größen in der Physik, wie zum Beispiel die Kraft und die Geschwindigkeit, weisen nicht nur einen Betrag auf, sondern haben auch eine Richtung. 1) Koordinatensystem und Darstellung eines Vektors. Wichtig ist dabei, dass die Einheiten auf der . Einteilung der x-Achse. Hierzu nehmen wir die Schnittpunkte der Ebene mit den Achsen des Koordinatensystems. Im sieht die Drehmatrix wie folgt aus:.com/c/EinfachMath. Der Verbindungsvektor beginnt dann bei A (Fußpunkt) und endet bei B (Spitze) . (00:43) Um einen Richtungsvektor zu berechnen, brauchst du die folgende Formel : Rechne immer B minus A, also „ Spitze minus Fuß „. Dass lässt sich besser im 2D- Koordinatensystem machen, aber denk dran, es funktioniert auch in 3D! Punkte im Koordinatensystem/ Punkte auf den Achsen & Koordinatensystem.Spiegelung Punkt an einer beliebigen Geraden, dazu muss man, die Normale von dem Punkt auf die Gerade fällen und Schneiden, dann den Vektor Punkt Schnittpunkt von P aus auf das doppelte verlängern. In der Ebene stehen die beiden x- und y-Koordinatenachsen orthogonal (in 90°) aufeinander, sie teilen die gaußsche Ebene in 4 Quadranten, die vom rechten oberen Quadranten „1“ ausgehend gegen den Uhrzeigersinn, von 1.

Ortsvektor: Definition, Bestimmen & Berechnen

Gehe von folgenden Ausmaßen aus: Länge: 10 LE. Es wird oft mit Fettschrift. (a) ★ Die folgende Abbildung zeigt ein Haus mit Walmdach. Gelegentlich findet man in der Formel die Koordinaten vertauscht, also zum Beispiel $(p_1-q_1)^2$.

• Wie Schneidet Man Ein Lavendel?
• Wie Schütze Ich Mein Handy Vor Spionage?
• Wie Schneide Ich Reben Richtig
• Wie Schmeckt Die Königskrabbe?
• Wie Schreibe Ich Das Perfekte Anschreiben?
• Wie Rollt Man Marzipan Aus | Wie rollt man Teig richtig aus?
• Wie Sollte Die Sprache Des Gedichts Analysiert Werden?
• Wie Schließe Ich Dlan An? _ Wie schließe ich mein Podcast-Setup richtig an?
• Wie Spricht Man Mit Pferden _ Koppen
• Wie Schreibt Man Gute Arbeitsanweisungen