Wie Beweisen Sie Eine Interpolationsbedingung?
Di: Samuel
Monotonie bestimmen: Schritt-für-Schritt Anleitung. Die Feinheit der gesamten Intervallunterteilung wird durch ., xk) den ( m + k + 1)-dimensionalen Raum der Splinefunktionen, d. Seine Erkenntnisse übertrug er auf den lotrechten Fall, da die Bewegung einer Kugel auf einer immer steiler geneigten . Zwei gegenüberliegende Seiten sollten Parallel sein. Lösungshinweise zum Übungsblatt Nr. Aktuelle Gerichtsurteile und ihre Auswirkungen auf das Beweisverfahren.Captchas: Wie beweisen wir in Zukunft, dass wir „keine Roboter“ sind? Artikel anhören • 6 Minuten.Spline-Interpolation Definition: Splineraum 7.Ein paar Beispiele für Liebesbeweise: Gut nach einem kleinen Streit: Ein Heftchen oder ein Box mit Gutscheinen machen, etwa „Gutschein für einmal Klodeckel oben lassen“ oder „Gutschein für einen Tanzfilmabend mit den Freundinnen“. Die Wahl der einfachen . Da der Nachweis einer Schenkung mit kaum überwindbaren Schwierigkeiten verbunden sein kann, trifft den Beschenkten eine erhöhte Darlegungslast. Dazu ließ er eine Kugel eine schiefe Ebene herabrollen und achtete dabei auf die Geschwindigkeit, die sie erreichte. [Hinweis: Beweisen Sie die Aussage zu nächst für den Fall k= 2. , kurz ü F r ü c k = − k ⋅ y.Die WENN-Funktion ermöglicht einen logischen Vergleich zwischen einem aktuellen Wert und einem erwarteten Wert. WENN (ein Wert wahr ist, tue dieses, andernfalls tue etwas anderes) Daher kann eine WENN-Anweisung zwei Ergebnisse . Sei V = ℝ und f : V → V gegeben durch f(x) = df 2x + 3.
Mathematisch Beweisen
Viele Professoren unterstellen ihren Mathe-, Physik- und Informatikstudenten (und wer Beweise sonst noch benötigt) anscheinend, dass man . Umso länger man zueinander Kontakt hat umso mehr zeigt man den anderen das man es ernst meint. Ob eine Schwingung harmonisch ist wird durch eine der beiden folgenden Bedingungen festgelegt. Zeigen Sie, dass G abelsch ist.An dieser Stelle haben wir eine weitere Technik verwendet, die sehr lei-stungsstark sein kann: wir haben uns nicht die gesamte rechte Seite als Ganzes angeschaut, sondern erst mal nur einen Summanden davon, n amlich ab.Sie können UND, ODER und NICHT auch verwenden, um Kriterien für die bedingte Formatierung mit der Formeloption festzulegen.
Harmonische Schwingungen
Doch neue Technologien machen diese Tests unwirksam – und barrierefrei sind sie oft auch nicht. ? Siehe Steigung im Wiki 2 Antworten + 0 Daumen.FRAGE 1: Wie komme ich jetzt darauf, dass 3 ein Teiler von a ist? ohne konkret die Frage 1 beantworten zu können, habe ich folgende Gleichung: a=3*x.Um zu zeigen, dass ein Raum X vollständig ist, reicht es, wenn du einen der folgenden beiden Aussagen beweist (beide Aussagen sind äquivalent): Jede Cauchy-Folge (xn)n ∈ N aus X ist eine konvergente Folge. Das globale Intervall (wie vorher [a,b] =: I) wird in Teilintervalle Ii = [xi−1,xi] mit der Länge hi = xi−xi−1 unterteilt.+anxn, das die gegebenen Daten interpoliert, so dass pn(xi) = fi, 0 ≤ i ≤ n. Die Umkehrung dieser Aussage ist ebenso wahr.
Abelsche Gruppe beweisen
le schöne Sätze darüber beweisen kann. Dazu wird auf eine Bedingung geprüft und ein Ergebnis zurückgegeben, wenn der Wert wahr oder falsch ist. Dh lernt euch weiter kennen, trefft euch weiterhin und zeige ihm so, dass er dir wichtig ist.Sie regelt die Frage, wer im Streitfall die Beweislast für die behaupteten Tatsachen trägt und damit das Prozessrisiko übernimmt.Einführung ins Beweisverfahren: Bedeutung und Ziel. Also all die kleinen Streitigkeiten und Konfliktpunkte in der Beziehung. mit bestimmten Leistungen seine Fähigkeiten, seine Befähigung für etwas unter Beweis . Q ist notwendig und hinreichend für P.orkursV Mathematik, PD Dr.O ist eine beliebige Vereinigung offener Mengen.
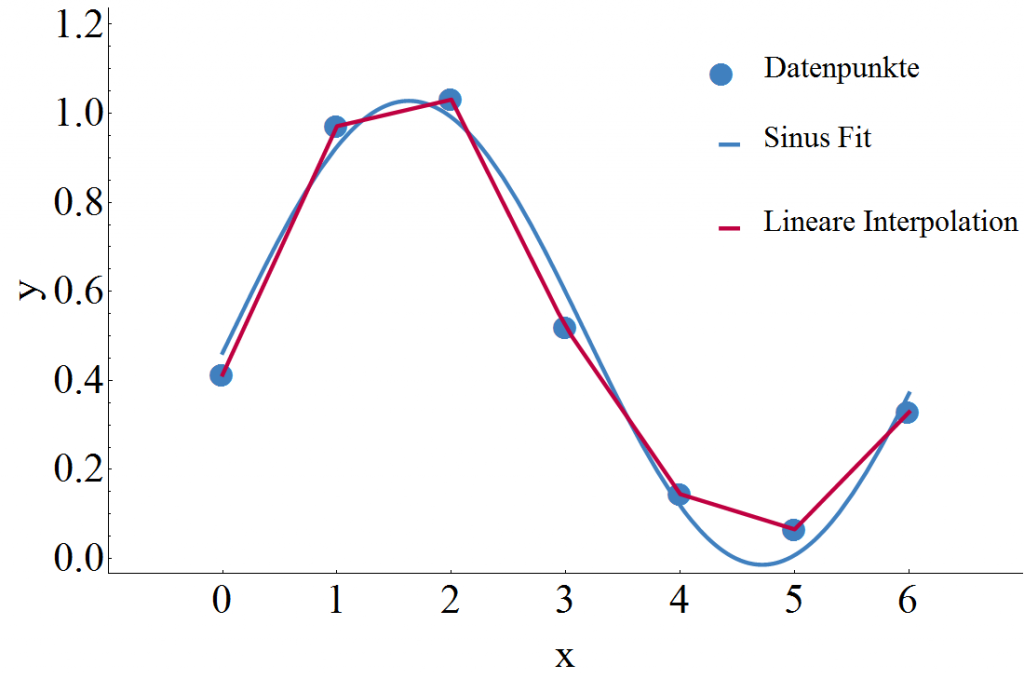
Wenn eine mathematische Aussage bewiesen werden soll, dann ist es günstig, diese . Dazu musst du zeigen: 1) Induktionsbasis: A (0) ist wahr. Wie beweist man, ob eine Abbildung linear ist oder nicht? Geben Sie in jeder der folgenden Teilaufgaben an, ob die Abbildung f linear ist. Es ist nämlich. Die blaue, linke Fläche entspricht (b-a)*1 Und die rosa, rechte Fläche entspricht dem Wert 0, da obere und untere Fläche sich weg heben. Aufgabe: Sei (G,∗) eine Gruppe.
INTERPOLATION
a) Die Funktion s ∈ Ck−1(R) heißt Splinefunktion vom Grad k mit Knotenvektor T, falls die Einschr¨ankungen
Wie beweise ich jemandem meine liebe?
Aus eine Ich wird ein Wir. 1 ≤ i ≤ k} abzählbar ist.Es gibt drei unterschiedliche Fälle für Symmetrien, die Teil der Analysis sind: Wenn Du eine Funktion drehst, spiegelst oder verschiebst und die Funktion nach wie vor seine Form beibehält, handelt es sich in der Analysis um eine Achsen-bzw. (00:14) Eine Orthonormalbasis (oft mit ONB abgekürzt) ist eine Basis eines Vektorraumes, wobei deren Basisvektoren orthonormal zueinander sind.Harmonische Schwingungen. Durch Beschreibung der Vektoren . Sei (G,\circ) (G,∘) eine Gruppe, H\subseteq G H ⊆ G eine nichtleere Teilmenge von G G.
FRAGE 2: Warum bzw. Kausalität bedeutet, dass eine eindeutige Ursache-Wirkungs-Beziehung zwischen zwei Variablen besteht.Differenzierbarkeit ist eine wichtige Eigenschaft von stetigen Funktionen.
Was ist ein Untervektorraum und wie kann ich es beweisen?
Klicken Sie auf der Registerkarte Start auf Bedingte Formatierung > Neue Regel.] (c) Beweisen Sie, dass die Menge aller endlichen Teilmengen von N abzählbar ist. Messwerten) soll eine stetige Funktion (die sogenannte Interpolante oder Interpolierende) gefunden werden . Aufgabe 1: ormFulierung direkter Beweise Zeigen Sie: 1. Erster L¨osungsansatz: Die Interpolationsbedingungen ergeben lineares SystemBewertungen: 232Der Pflichtteilsberechtigte trägt grundsätzlich die Beweislast für eine von ihm behauptete Schenkung.Für jede natürliche Zahl n sind n2+n und n2n .4: SplineInterpolation. Es handelt sich um vier Axiome für die Addition und vier Axiome für die Skalarmultiplikation.Eine Reihe konvergiert, wenn die Folge der Partialsummen konvergiert. In diesem Fall können Sie UND, ODER und NICHT eigenständig verwenden und auf die Funktion WENN verzichten., m k);m i ∈ M i für. Laut Definition ist ein Vektorraum über einem Körper eine Menge mit zwei Verknüpfungen , der Addition, und , der Skalarmultiplikation, die eine Liste von Axiomen erfüllen. f(x) I i y i a = x0 x i−1 x i b = x n y i−1 Abbildung 3.

250 Personen in der Mensa. Verneinung: Für mindestens ein x gilt, dass x > 5. f ist injektiv: für u,v ∈ A muss dann gelten: u ≠ v ⇒ f(u) ≠ f(v) damit gleichwertig ist die Kontraposition: f(u) = f(v) ⇒ u = v.Oszillationen am Rand des Intervalls, wie sie in Beispiel 3. In einigen Fällen können jedoch gesetzliche oder richterliche Regelungen die Beweislast auf die andere Partei übertragen. Der Vorteil ist, daˇ dieser nur aus zwei Variablen besteht (aund b, aber nicht c), was ubersichtlicher und einfacher zu . Wenn du eine Funktionsgleichung hast schreibst du also die linke Gleichung hin und vereinfachst sie ggf. Beispielbeweis: Die Menge O = {(x, y) ∈ R2: ∃m, n ∈ Z‖(x, y) − (m, n)‖ < 1 2} ist offen in M = R2 bzgl der durch ‖ ⋅ ‖ erzeugten Metrik. Spline-Interpolation.

Ich schreibe nächste Woche Mathe Abitur und wollte mich vergewissern, ob folgende Bedingungen ausreichend, um festzustellen das es sich bei den Körper um folgende handelt. Aussage: Es gibt (mindestens) ein x mit x > 2 Verneinung: Für alle x gilt x ≤ 2.,n,mitpaarweise . Es seien k, m natürliche Zahlen, a = x0 < x1 < . Das heißt das Skalarprodukt zweier beliebiger Basisvektoren ergibt Null und jeder Basisvektor besitzt die Norm 1. Nächste » + 0 Daumen.Beweisen Sie, dass auch M 1 ×M 2 ×.Lexikon der Mathematik Spline-Interpolation.
Konvergenz und Divergenz beweisen
Interpolation (Mathematik) In der numerischen Mathematik bezeichnet der Begriff Interpolation (aus lateinisch inter = dazwischen und polire = glätten, schleifen) eine Klasse von Problemen und Verfahren.was zu beweisen war (bekräftigende Schlussformel nach einem durchgeführten Beweis) einen Beweis (2) von etwas geben; erkennen lassen, zeigen.Ist (V,+,*) ein Vektorraum über einem Körper K, so bildet eine Teilmenge U von V genau dann einen Untervektorraum von V, wenn sie nichtleer und abgeschlossen bezüglich der Vektoraddition und der Skalarmultiplikation von V ist. Rechteck – 4 rechte .Ablesen der Regressionsgeraden ergibt eine Schätzung von ca. steigung; trapez; Gefragt 6 Mär 2015 von Gast. Wir sprechen dabei vom sogenannten linearen Kraftgesetz. Um festzustellen, ob eine Teilmenge U von V ein Untervektorraum von V ist, ist also zu prüfen: U\neq . Schritt 1: Berechne die erste Ableitung . Es werden Beispiele von Unterräumen spezieller Vektorräume angeführt.
Induktion: Die Potenzmenge einer Menge mit n Elementen hat 2
Beweisanträge: Form und Inhalt. Liebe beweist man wenn dann über Zeit. Das erste Ergebnis wird ausgegeben, wenn der Vergleich wahr ist, das zweite, wenn der Vergleich falsch ist. das setze ich in 3b²=a² ein –> (3*x)²=3b² –> 9x²=3b² –> 3x²=b².
WENN-Funktion
Theoretisches Material und Übungen Mathematik, 6. Dies bedeutet, dass du für jede Cauchy-Folge (xn)n ∈ N einen Wert x ∈ X finden musst, so dass x Grenzwert der Folge (xn)n ∈ N ist .ich weiß leider nicht, wie folgende Aufgabe funktioniert. Bestimme ein Polynom (h¨ochstens) n-ten Grades pn(x) = a0 +a1x+a2x2 +. Jedoch bräuchte ich einen Denkanstoß, wie ich eine abelsche Gruppe . Das Integral zwischen a und b gibt den Flächeninhalt der Kurve an, die zwischen f(x) und der x-Achse eingeschlossen ist. Konvergenzsätze Der Satz über monotone Konvergenz ist Beppo Levi bzw. seine Ablehnung beweist nur seine mangelnde Einsicht.
(b) Spline-Interpolation
und auch hier wieder, 3 ist Teiler von b².
Ungleichungen
Allgemein nennst du eine Funktion an der Stelle x 0 differenzierbar, wenn dieser Grenzwert existiert: Das bedeutet, er ist . Sei (fk) eine monotone Folge integrierbarer Funktionen fk ∈ F(Rn). Es liegt also eine Kausalität vor, wenn Handlung A das Ergebnis B verursacht. Ansonsten divergiert die Reihe.Der erste echte Leitfaden für mathematisches Beweisen. Ablauf des Beweisverfahrens: Schritt für Schritt.sei f: A → B eine Funktion.
Beweise von abzählbaren mengen
Abelsche Gruppe beweisen. zur Stelle im Video springen.Jede ungerade natürliche Zahl ist Di erenz zweier Quadratzahlen. Hallo Samira, du willst folgende Aussage A (n) beweisen: Für alle n ∈ ℕ0 gilt: Jede Menge mit n Elementen hat 2n Teilmengen. Quadratur als Flächenberechnung.
Henri Lebesgue zugeschrieben. Schritt 3: Du erstellst eine Vorzeichentabelle mit den Extremstellen .

Orthonormalbasis einfach erklärt.
Notwendige und hinreichende Bedingung
Jeder Beweis besteht aus drei Schritten, die schon von EUKLID so angegeben wurden, nämlich.Die WENN-Funktion ist eine der am häufigsten verwendeten Funktionen in Excel. Sei f ∈ F(Rn) der punktweise Limes f = limk fk. < xk < xk+1 = b, eine Knotenmenge und es bezeichne Sm ( x1, . Beliebt sind sie nicht, aber oft noch notwendig: Captchas, mit denen Menschen im Internet unter Beweis stellen, dass sie ebensolche sind. die Menge der ( m − 1)-fach . Erfüllt eine Schwingung eine dieser beiden Bedingungen, so erfüllt sie immer auch die andere.46 Kapitel 2: Interpolation Wie angeku¨ndigt, liefert die Lagrange-Darstellung einen konstruktiven Beweis fu¨r die Existenz und Eindeutigkeit eines Polynoms P(x),dasdieInterpolationsbedingung(2.Man unterscheidet im Wesentlichen zwei Beweisverfahren, den direkten Beweis und den indirekten Beweis. Danach ist er verpflichtet, alle Tatsachen für die fehlende Unentgeltlichkeit ausführlich vorzutragen und . Beweisverwertung und strafrechtliche . Die Betrachtung der Bedingungen der Vektorraumdefinition führen zur Definition eines Unterraumes sowie dem Unterraumkriterium und weiter zum Begriff des Erzeugendensystems.Geometrie: mithilfe Vektoren nachweisen, dass es eine Raute / Rechteck / Quadrat / Parallelogramm. Wenn a n-1 (mod n) = 1 (mod n), dann ist n eine mögliche . Wenn ja, beweisen Sie ihre Aussage.1 (Satz über monotone Konvergenz). Ein vollständiger Beweis muss auch im Umkehrschluss zu richtigen Aussagen . Die verschiedenen Arten von Beweisen. Im Fall der Konvergenz entspricht Ansonsten divergiert die Reihe. Schritt 2: Bestimme die Nullstellen von . Man betrachte nur die natürlichen Zahlen \dom N N als . Uns interessiert die Symmetrie hauptsächlich als Teil der Analysis, aber auch .5 (Existenz und Eindeutigkeit derLagrange-Interpolation) Zu beliebigen (n +1) Paaren (xi,fi),i=0,. Problem/Ansatz: Hallo kann mir jemand mit den beweisen dieser 3 aufgabenteile helfen.Aussage: Für alle x gilt x ≤ 5 . Sie ermöglicht den logischen Vergleich zwischen einem aktuellen Wert und einem erwarteten Wert. Wir haben auch aktuelle Gerichtsurteile präsentiert und einige häufig gestellte Fragen zum Thema beantwortet. Probable-Primality (Mögliche Primzahlen): Die zu überprüfende Primzahl n > 1; eine beliebige Ganzzahl a > 1. Grundsätzlich hat die Darstellung als einfache Funktion den groen Vorteil, dass Elemen-taroperationen (wie bei der Interpolation bereits angemerkt), wie Ableitungsbildung und Integration, viel einfacher ausgeführt werden können.Unterräume und Erzeugendensysteme.In diesem Kapitel wird erläutert, wie man die Konvergenz und Divergenz einer Folge beweisen kann.In diesem umfangreichen Beitrag haben wir die Grundlagen mündlicher Verträge untersucht, darunter ihre Gültigkeit, ihre Durchsetzung, die damit verbundenen Risiken und die gesetzlichen Voraussetzungen, denen sie unterliegen. Die ROLL-Regel und ihre Wirkung auf das Beweisverfahren.Allgemeine Beweisstruktur [Bearbeiten].Zu beweisen, daþ eine Zahl eine Primzahl ist, wenn sie die Prüfung besteht, ist nicht m–glich, da dieser Satz noch nicht in seiner Umkehrung bewiesen werden konnte. Daher kann eine WENN-Anweisung zwei Ergebnisse haben.Diese sind im Artikel Vektorraum aufgelistet. Für alle a ∈ G gelte a ∗ a = e. Notwendige und hinreichende Bedingung. Wenn x gerade (durch 2 teilbar) und durch 3 teilbar ist, dann ist x auch durch 6 teilbar.
3 Interpolation und Approximation
2) Induktionsschluss: A (z) ⇒ A (z+1) [ Wenn A (z) für irgendein z ∈ ℕ0 wahr ist, dann ist auch A (z+1) wahr ] Nachweis: Theoretisches Material zum Thema All- und Existenzaussagen. Im Fall der Konvergenz entspricht ∑ k = 1 ∞ a k {\displaystyle \sum _{k=1}^{\infty }a_{k}} auch dem Grenzwert der Partialsummenfolge. Voraussetzung – Behauptung – Beweis (durchführung).×M k ={(m 1, m 2, . Problem/Ansatz: Ich weiß, dass abelsche vom Kommutativgesetz, Assoziativgesetz, inversem Element und neutralem Element abhängig ist. sind sehr nützlich. Die Konvergenzsätze z. Sie entsteht erst im Laufe einer Beziehung. Zu gegebenen diskreten Daten (z.
Differenzierbarkeit • Defintion, Beispiele, Methoden · [mit Video]
Wenn nein, geben Sie ein Gegenbeispiel an. Ein häufiger Fehler bei der Interpretation von Statistiken ist, dass bei Vorliegen einer Korrelation auf eine Kausalität geschlossen wird. (01:45) Um das Monotonieverhalten einer Funktion f (x) zu bestimmen, folgst du am besten folgender Anleitung. 3, Besprechung am 15. Wenn H H bezüglich \circ ∘ eine Gruppe ist, so heißt (H,\circ) (H,∘) Untergruppe von (G,\circ) (G,∘).
Untergruppen
Normalerweise teilt sich diese Arbeit in zwei Arbeitsschritte auf: Zunächst versucht man auf einem Schmierblatt, eine Beweisidee zu finden, die man danach im zweiten Schritt in einem Beweis umsetzt und ins Reine schreibt. sie hat bei dem Unglück große Umsicht bewiesen. so, das sich u = v ergibt. Eigentlich erschreckend, doch es gibt bisher tatsächlich keine wirklich gute Anleitung dafür, WIE man an einen mathematischen Beweis herangeht. der Operation \circ ∘ eine Gruppe sein. Nicht jede Teilmenge muss bzgl. ( ω ⋅ t) beschrieben werden.
Wie rechnerisch ein Trapez beweisen?
Halupczok, WWU Münster, acFhbereich Mathematik und Informatik 15. Grundsätzlich gilt dabei: Wer eine Tatsache behauptet, muss sie auch beweisen.

Um das zu beweisen, experimentierte er mit einem sogenannten „verlangsamten freien Fall“.Kapitel 8: Interpolation Klassische Polynom-Interpolation. wie begründe ich auch hier warum 3 ein Teiler von b? Du kannst eine nicht differenzierbare Funktion an einem Knick in ihrem Graphen erkennen: Differenzierbare und nicht differenzierbare Funktion. Es ist also O eine Vereinigung offener Mengen und damit wieder offen (mach dir eine Skizze zu diesem Beispiel). Theorie der Interpolation mit Splinefunktionen. Punktsymmetrie.1 Definition: Splineraum Gegeben seien k ∈ N 0 und T = {t 0