Wie Berechnet Man Die Fourierreihe?
Di: Samuel
In den Beispielen wurden alle Funktionsdefinitionen so gewählt, dass sie, unabhängig vom gewählten Intervall, Die Fourierreihe mit den diskreten Koeffizienten cn geht über in ein Integral mit einer kontinuierlichen Amplitudenfunktion C(f) bzw.
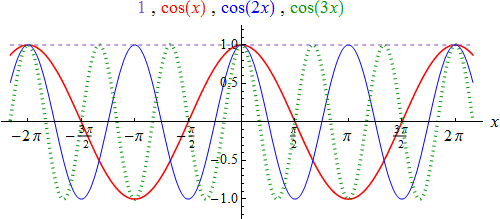
Die Fallbetrachtungen und Berechnungen erfolgen nur . Wechselt man anschließend das Intervall, so wird sich meistens eine andere Fourierreihe ergeben.nachdem ich die Fourierreihe einer Rechteckschwingung und die einer Sägezahnschwingung berechnet habe, soll ich nun die Fourierreihe zu einer Dreieckschwingung berechnen.Fourierreihen Einer auf dem Intervall [ˇ; .Die Funktion f (x) ist definiert durch: Um diese Funktion in einer Fourierreihe darzustellen, müssen wir die Fourier- koeffizienten berechnen. x (t) = 1-|t| für -π<= t < π. Wird die Fourierreihe mit der Sinusfunktion multipliziert, so hat in Analogie zur Herleitung oben das linke Teilintegral immer den Wert null. (anders geschrieben) Für einige Folgen lassen sich relativ leicht Formeln zur Berechnung ihrer Partialsummen angeben. fourierreihe; komplexe-zahlen + 0 Daumen. Für a0 berechnen wir: Für die restlichen . Es gilt nämlich c−i = ci * . a) In jedem Stetigkeitspunkt x gilt Sn(x)! f(x) .Ich weiss nicht was Du damit meinst. (Für Korrekturen bin ich dankbar!1) Es darf nur .L asst man nun n!1gehen, so erh alt man die Gleichung X1 i=0 qi= 1 1 q. 74 haben wir ausführlich beschrieben, wie man die Fourierreihe F zu einer Funktion \(f \in C(T)\) bestimmt. Gefragt 6 Nov 2019 von Cookie. Wir haben also die Integrale an = 1 π π/2 0 dx cosnx + 1 . Beantwortet 13 Jun 2020 von lul 106 k ?. Die Funktion lässt sich in eine Fourierreihe entwickeln, dass muss Du nicht mehr beweisen, sondern nur noch die Koeffizienten berechnen. Konvergenzbedingungen fur Funktio-nen f: R !C oder die Exponentialschreibweise fur Sinusfunktionen.
Definition der Fourierreihe
Dann heißen die in (2) und (3) definierten Zahlen die Fourier-Koeffizienten von f f.
Wie berechnet man die Fourrier-Koeffizienten?
tր lim f(t) +. Definition: Die Fourierreihe eines periodischen Signals x(t) lautet wie folgt: x(t) = A0 + ∞ ∑ n = 1An ⋅ cos(nω0t) + ∞ ∑ . Es können allgemeinere Typen von Funktionen in eine Fourier-Reihe entwickelt werden, so abschnittsweise .3 Konvergenzverhalten von Fourierreihen 25 Ist P 1 k=0 a k eine Reihe von reellen . [vorangehende Seite] [nachfolgende Seite] [Gesamtverzeichnis][Seitenübersicht] . Wir schildern diese Berechnung der Fourierkoeffizienten und stellen so periodische Funktionen aller Couleur als . Mit der Grundfrequenz = / und den Kreisfrequenzen = gilt: ^ = () = = ^. Ebenso ist dies kein verifiziertes, autorisiertes oder offizielles Skript. Das Signal wird 2pi- periodisch fortgesetzt. Wir müssen daher nur die Koeffizienten an bestimmen.Wie macht man das? Fourier- Reihe Zerlegung einer periodischen Funktion in ihre sinus- und cosinus-förmigen Anteile ( ) 0 ( ) k cos(k) k sin(k) k f t A ωt B ωt ∞ = =∑ + Technik der Fourier-Transformation Fourier-Reihen Voraussetzungen: Periodische Funktionen gerade: z.Die Mathematik hinter dieser Zerlegung ist dabei das Berechnen der Fourierkoeffizienten zu den Grundschwingungen.Im Rahmen der Theorie der .
Fourierreihen
Willkommen bei der Mathelounge! .Wie komme ich an die Koeffizienten ran? (Wann) konvergiert die Fourier-Reihe (punktweise oder gleichmaßig)?¨ Analysis I June 21, 2018 163 / 173.
Überlagert man harmonische Schwingungen der gleichen Frequenz, so erhält man wieder eine harmonische Schwingung derselben Frequenz. Das habe ich auch so gemacht, um das Bild zu erstellen.Die Fourierreihe (reell) für die Dreiecksschwingung (achsensymmetrisch) der Periodendauer 2Pi wird berechnet.Setzt man diesen Vorgang fort, geht die Periodendauer gegen Unendlich und der Frequenzabstand der diskreten Frequenzen geht gegen Null: das Spektrum wird eine kontinuierliche Funktion. Die mit diesen Koeffizienten gebildete trigonometrische Reihe. Die obige Schreibweise ist ¨ublich, wenn es sich bei x um eine Ortsvariable handelt. Da die Rechteckfunktion gerade.Normalerweise enscheidet man sich zuerst, ob man ein Intervall [-L,L] oder [0,2L] nutzen möchte. Ist die unabh¨angige Variable die Zeit t, so wird f¨ur die L ¨ange des Grundintervalls T verwendet, und an die Stelle der Wellenzahlen kn treten die diskreten Frequenzen ωn = n∆ω mit ∆ω = 2π/T. Sei f\in \mathcal R [-\pi,\;\pi] f ∈ R[−π, π]. Hast Du die Koeffizienten berechnet, kann man die Reihe numerisch auswerten. Teil 1 ist bis zur Berechnung des Fourier-Koeff.Verwandte Videos:Fourierreihen: Eine Einführung: https://youtu.
Fourier‘sche Reihenentwicklung
Für jedes n kann die Fourierreihe durch ein entsprechendes Fourier Integral geschrieben werden. Integriert wird in den Grenzen einer Periodendauer T. Zum Beispiel ist das der Fall, wenn die Koeffizienten Ausdr¨ ¨ucke wie 1 k¡1 oder 1 k2¡3k+2 enthalten, dann gelten sie erst ab k = 2 bzw. Führt der Computer die Berechnung mittels herkömmlicher .To find the amplitudes of the three frequency peaks, convert the fft spectrum in Y to the single-sided amplitude spectrum. Hierbei ist von großer Bedeutung, wie viele Rechenoperationen der Computer dazu ausführen muss.Es werden die Koeffizienten der Fourierreihe berechnet und die Funktion wird grafisch dargestellt. Ich verwende in diesem Kapitel die symmetrische, in der Mathematik übliche Normierung √ 2π. heißt die zu f f gehörige Fourier-Reihe.Die Basisfunktionen der Fourierreihe bilden ein bekanntes Beispiel für eine Orthonormalbasis.Aus (5) folgt, dass sich die ci für i 0 berechnen lassen.Das Berechnen der einzelnen harmonischen Funktionen, die – durch Überlagerung (Summation) – eine vorgegebenen periodischen Funktion annähern, nennt man Fourier Analyse. Es soll das Frequenzspektrum . Das ist kein Zufall, sondern eine Folge der Tatsache, dass die Fourierreihe hier (bei angenommener stetiger Differenzierbarkeit von f) gegen f konvergiert.
7 Fourier-Transformation
Die Schwierigkeit besteht . (6) Daher brauchen zur Berechnung der komplexen Fourier-Reihe einer reellwertigen Funktion f(t) zunächst nur die ci für i ≥ 0 berechnet zu werden. Als Fourierreihe, nach Joseph Fourier (1768–1830), .Anstatt die Fourier-Reihe wie gewohnt zu berechnen, berechnet man ein Integral in Zeitbereich: das Fourier-Integral kann verstanden werden, falls man denkt an einer Funktion dessen Periode gegen 1geht. Hierbei ist A die Amplitude, ω die Kreisfrequenz und \(\varphi\) der Phasenwinkel.2) y = 1 f¨ur 0 Bei der Überlagerung derartiger harmonischer Schwingungen sind zwei Fälle zu unterscheiden: 1. orthonormalbasis; komplexe-zahlen + 0 Daumen.Kostenloser Fourier-Reihen-Rechner – Finden Sie die Fourier-Reihen von Funktionen Schritt für Schritt f(t) = 2π −∞ −∞ f(τ)eiω(t−τ) dτ dω.Formeln für die Berechnung der fourierschen Koeffizienten. Man spricht von der geometrischen Reihe\. Wie berechnet man die i. Dies illustriert die Anwendung der Fourier-Transformation zur Analyse der Frequenzanteile von Signalen – hieraus leitet sich auch das Synonym Spektralfunktion für die Fourier-Transformierte ab.(c) Man erkennt, dass man in (a) und (b) dasselbe für die Fourierkoeffizienten herausbekommt. Jede periodische Funktion x(t) kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet. \(f(x) = F(x)\).Ich habe versucht, alles richtig wie-derzugeben, diese Mitschrift erhebt allerdings keinen Anspruch auf Vollständigkeit noch auf Rich- tigkeit (Irren ist menschlich).Heuristisch wird so aus der Fourier–Reihe das # Fourier–Integral: g(ξ) = ˆ ∞ x=−∞ e−ixξf(x)dx und f(x) ∼ 1 2π ˆ ∞ ξ=−∞ g(ξ)eixξdξ Diese Formel mit 2πvor dem letzten Integral ist die Konvention der Physik, siehe Laplace L406. Falls f bei t0 ∈. Beispiel: reelle und komplexe Fourier-Reihe der Funktion f(x) = sin4 x + cos3 x x 0 1 gerade Funktion f(x) = (1 cos2 x)2 + cos3 x = 1 2cos2 x + cos3 x + cos4 x Umwandeln von cos‘ x in Linearkombinationen von cos(kx) Zusammenhang .Definition Fourierreihe. Komplexe Form: Fourier-Reihen können zudem mit Hilfe komplexer Zahlen beschrieben werden: Eine Einsicht darüber erlangt man, indem man die Summe aufteilt: Durch Koeffizientenvergleich erhält man: Es gilt: mit: T = 2 π / ω 0: Schwingungsdauer. Ich benutze hier einige Vorraussetzungen die der letzte Referent schon eingefurt und bewiesen hat, wie z.Wie bei der Berechnung der hier auftretenden Integrale am besten vorgegangen wird, hängt natürlich von der konkreten Funktion f ab, die in eine Fourierreihe entwickelt werden soll. S(x) = a0 2 + ∑1 k=1 ak coskx+ ∑1 k=1 bk sinkx (ak;bk wie zuvor angegeben) Satz.Die so (meist durch partielle Integration) erhaltenen Formeln sind aber oft erst ab k ‚ k0 gultig. Es sei auch noch an folgende Tatsachen erinnert: Ist bekannt, dass die Reihe P 1 k=0 a kkonvergiert, so muss die Folge (a k) gegen Null konvergieren. Als Beispiel f¨ur eine gerade Funktion betrachten wir die Rechteckfunktion (siehe Abb.Wie bestimmt man die Fourierkoeffizienten in einer Fourierreihe? Hier wird es erklärt. Sei f(x) stuc¨ kweise stetig differenzierbar und 2 ˇ-periodisch. Hast Du jetzt \( b_k . Wir betrachten dazu nachstehend zwei Beispiele.Mit den Umrechnungsformeln ergeben sich somit für die von null verschiedenen Koeffizienten der komplexen Fourier-Reihe .Hier wirst du nicht nur ihre Definition, Algorithmen und Grundlagen kennenlernen, sondern auch wie man sie berechnet und anwendet. Die Fourier Koeffizienten a k und b k entsprechen den Amplituden der entsprechenden Schwingungsanteile (so genannte Harmonische).Offensichtlich ben¨otigt man die h¨oheren Entwicklungskoe ffizienten fur die Darstellung sehr¨ kleiner Details wie z.Ich werde mich mit einer gr oˇeren Klasse von Funk-tionen, der der stuc kweise stetig di erenzierbaren Funktionen besch aftigen. Mathematisch bedeutsam sind die sogenannten Partialsummen von Zahlenfolgen. Dahinter verbirgt sich eine Skalarproduktbildung mittels eines Integrals. Wenn so etwas passiert, muss man die Koeffizienten f¨ur alle k, f¨ur die die allgemeine Formel nicht anwendbar ist, .Wie berechne ich die Fourierreihe dieser Funktion? f (x) = ( x – π / 2 )^{2 }für 0 ≤ x ≤ π. Orthonormalitat der Basisfunktionen¨ Buch Kap. The two-sided amplitude spectrum P2, where the . Deshalb stellt die Fourierreihe tatsächlich überall die Funktion f dar (und . analytisch berechnet werden. Fourierreihen Ahnlich wie im Cn k onnen wir auf L2 per ([ ˇ;ˇ]) ein Skalarprodukt de nieren. Integrale wie das eben benutzte von komplexwertigen Funktionen sind komponentenweise zu . Die n-te Partialsumme einer Zahlenfolge ist die Summe der Glieder von bis bzw. Positiver Teil des absoluten Betrags der Fourier-Transformierten.Die Fourier-Reihe ist genau dann reell, wenn c k = c k.Dann gilt die Fourier-Umkehrformel. cosinus ungerade: z. Zusammenhang komplexer und reeller Fourier-Reihen 1-2. Motivation: von .)? Gefragt 23 Nov 2023 von Rudstar. Wir de nieren das Skalarprodukt h:;:i : L2 per ([ ˇ;ˇ]) L2 per ([ ˇ;ˇ]) !C durch hf;gi L2:= Z ˇ ˇ f(x)g(x)dx: Bisher hatten wir nur reellwertige Funktionen integriert. In der Mathematik gibt es keine Autoritäten.Will man zu einer Funktion f die Fourierkoeffizienten a k und b k bestimmen, so ist es oftmals leichter, zuerst die komplexe Darstellung c k für \ (k\in {\mathbb {Z}}\) der Fourierkoeffizienten zu ermitteln und hieraus dann mit den angegebenen Umrechnungsformeln die Koeffizienten a k und b k zu erhalten.wie man die Fourrierkoeffizeinten bestimmt steht überall, bei pi und -pi hat man eine Sprungstelle von +1 nach -1 also muss man da f (x)=0 wählen.9 Satz Die Funktionen eik!t, k 2Z, != 2ˇ=T, bilden einOrthonormalsystem bezuglich des Skalarprodukts¨ hu;vi:= 1 T Z T 0 u(t)v(t)dt: Beweis . Fuhrt¨ man nun den Grenzub¨ ergang n ! 1 durch, dann erh¨alt man die der Funktion f(x) zugeordnete Fourier-Reihe. Danach legt man die Funktion f(x) fest. f (x) = f (-x), verschwinden alle Koeffizienten bn. R unstetig ist, so liefert das Doppelintegral auf der rechten Seite der Fourier-Umkehrformel den Mittelwert des links- und rechtsseitigen Grenzwertes von f f ̈ur t Z ∞ ∞. fourierreihe; monotonie; reihen; funktion; fourier; News AGB FAQ Schreibregeln Impressum Datenschutz Kontakt Liebe ist wie die Zahl Pi – positiv, irrational und sehr, sehr wichtig. Alternativ zu Datenpunkten kann die Entwicklung auch an eine Funktion erfolgen. Das Fourier-Integral einer nicht-periodischen Funktionf(x) ist gegeben durch f(x) = Z 1 0 [A(!)cos(!x) + B(!)sin(!x)]d! wobei . Wie berechnet man Potenzen von komplexen Zahlen? ( 1-i)^21 . Für die Fourier Koeffizienten gilt, dass sie für \(k \to \infty \) gegen Null konvergieren, gleichzeitig geht auch der Restfehler (also . der scharfen Ecken der S¨agezahnfunktion. Zudem wird dir die Teile und herrsche Methode im Kontext der schnellen Fourier Transformation vorgestellt und du erhältst einen detaillierten Vergleich zwischen der diskreten und digitalen schnellen Fourier . sinus „weder, noch“ : z.Jede stetig differenzierbare Funktion, die auf dem Intervall [,] definiert ist, lässt sich in eine Fourierreihe entwickeln, das heißt, beide Seiten der Transformation existieren.Sie werden aus nachfolgend aufgeführten Integralen berechnet: 2. Es gilt De nition 1. Wie berechnet man die Orthonormalbasis von Vektoren mit i? Gefragt 16 Dez 2015 von Gast. Because the fft function includes a scaling factor L between the original and the transformed signals, rescale Y by dividing by L. Soll für ein gemessenes Signal eine Spektralanalyse von einem Computer durchgeführt werden, so muss dieser die Diskrete Fourier Transformation durchführen. Alternativ kann man die komplexe Entwicklung auch mit Hilfe der Formeln von Euler-Moivre, herleiten. Damit man diese . Online Rechner Fourierreihe Rechner zur Fourierreihenentwicklung an beliebige Messwerte oder Funktionen. Setzt man die Berechnungsvorschriften für die ai und bi Um für eine konkrete gegebene periodische Funktion die Fourierreihe bilden zu können, sind deren (Fourier)Koeffizienten a 0, a k und b k zu bestimmen. Wenn f(x) im Intervall [−L/2,L/2] stetig ist und die .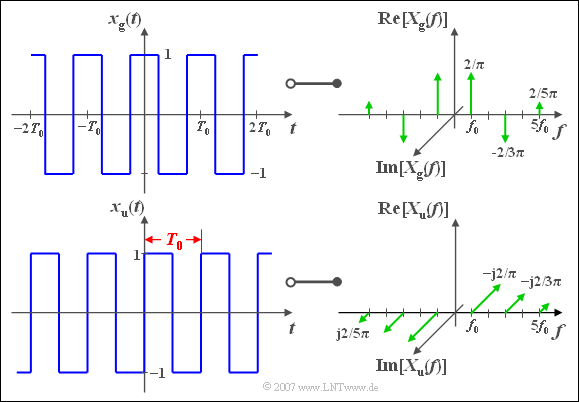
FFT (Fast Fourier Transformation) · Berechnung · [mit Video]

Fourier-Reihen
Hoehere Mathematik 3 (vertieft)
![Fourierreihen – einfach erklärt für dein Maschinenbau Studium · [mit Video]](https://d1g9li960vagp7.cloudfront.net/wp-content/uploads/2018/09/Gibb´sches-Phänomen_SEO-1024x576.jpg)
Fourier-Reihe (FR)
Fourier-Analysis
Kapitel6 Fourierreihenund Fourierintegrale
Fourier-Reihen-Rechner
Fourierreihen: Was das ist und wie man sie bestimmt
Berechnung der Fourier-Reihe für die Dreiecksfunktion (Teil 1, a
Fourierreihe
Fourier Transformation
Technik der Fourier-Transformation
Anhang 4: Spektrale Darstellung, Spektrum, Fouriertransformation
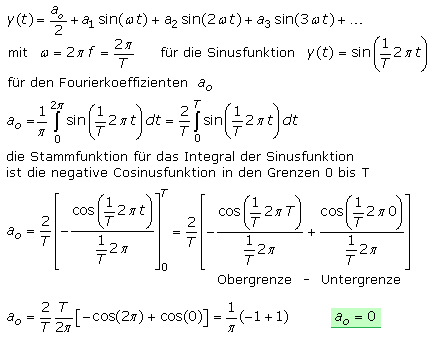

Fourierreihe