BAHTMZ

Why Does Pythagoras‘ Theorem Allow Construction Of Incommensurable Lengths?

Di: Samuel

The hypotenuse is the longest side, opposite the right angle.Not knowing the Pythagorean theorem can also be applied to other shapes An application of Pythagorean theorem is to extend it to work on other shapes such as a trapezoid.

TIMES MODULE M15

Why does the pythagorean theorem work?

First of all, I hope the above equations are right, as I feel like I’m messing up with the different notations. It is roughly equal to 1. Inside this blue square, the 4 hypotenuses create a black square of side length c (or area of c^2). There is a combination of lines whose squares happen to add up in this way, we call it a triangle. Additionally, this is also useful in woodworking and other physical object .Pythagorean Theorem. This means that the Pythagorean theorem was initially about the Pythagorean equality \(a^2+b^2=c^2\). The square drawn on the diagonal. The most basic relationship between the lengths of the sides is probably the triangle inequality, and for something specific to right . The Pythagorean theorem describes a special relationship between the sides of a right triangle.

Created by Sal Khan. Euclid gave two proofs of it in the Elements, as Proposition I,47, and also as Proposition VI,31, a more general but less well-known formulation concerning arbitrary .This is the best explanation I have seen of why intuitively the pythagorean theorem works: .The reason for this is that the theorem is only applied to right triangles, and that all squares whose sides were used as basis were all perfect squares.The Pythagorean theorem allows us to calculate the length of the diagonal that connects two straight lines that form a right angle. For four dimensions, you can imagine further going in a direction perpendicular to the other three dimensions .

When to use a squared B squared C squared?

This equation allows you to find the length of a side of a right triangle when they’ve given you the lengths for the other two sides, and, going in the . Pythagoras’ theorem was known to ancient Babylonians, Mesopotamians, Indians and Chinese – but Pythagoras may have been the first to find a formal, mathematical proof.Record Pythagoras’ Theorem on the board and ask the class to provide an example of a right-angled triangle with correct side lengths. Euclid was the first to mention and prove this fact.Using Equation (1) above arc length = ∫x1 = a1 x1 = a0√1 + x 2 2 x 2 1 + x 2 3 x 2 1 ⋅ dx1.Pythagoras’ theorem is used in determining the distance between two points in both two and three dimensional space. Which is the Pythagorean formula in 3 dimensions. Moral 2: Eudoxus‘ theory allows one to use numerical ratios to study geometric ratios, but it does not require the concept of an irrational number. This number is an irrational number, which means it goes on forever and can’t be written as a fraction.

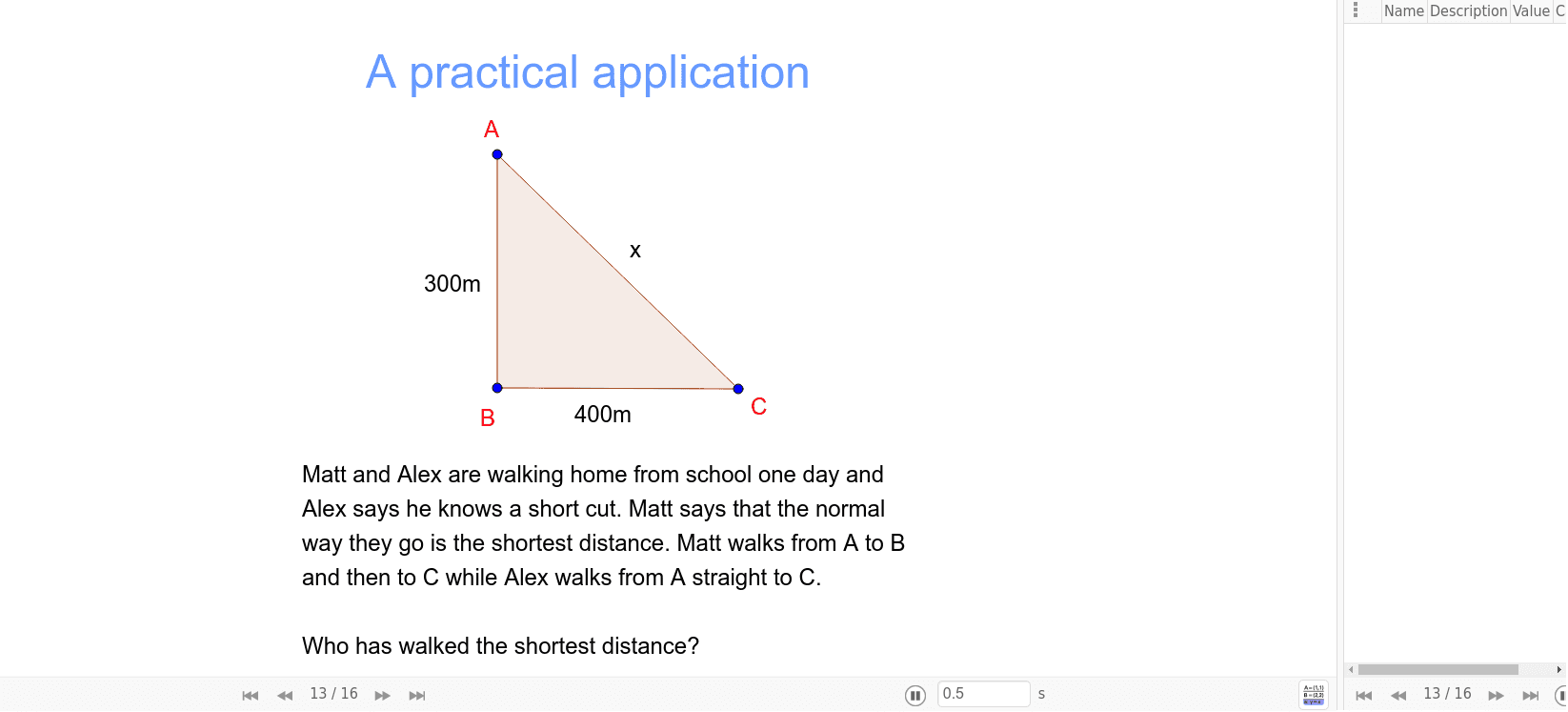
EDIT: 4th bullet point is important too . Here, AB is the base, AC is the altitude (height), and BC is the hypotenuse.The first proof of the existence of irrational numbers is usually attributed to a Pythagorean (possibly Hippasus of Metapontum), [39] who probably discovered them while identifying sides of the pentagram.

Although the theorem has long been associated with Greek mathematician-philosopher Pythagoras . This is used when we are given a triangle in which we only know the length of two of the three sides. The Pythagorean Theorem, also known as Pythagoras theorem is a mathematical relation between the 3 sides of a right triangle, a triangle in which one of 3 angles is 90°.The Incommensurability of Scientific Theories. The idea has its origins in Ancient Greek mathematics, where it meant no common measure between magnitudes. In fact, it became possible to create the unified theory of particles of The Pythagorean theorem states that in a right triangle, the sum of the squares of the two shorter sides equals the square of the longest side (the hypotenuse).In this video, I show how to calculate the length of a line segment on a grid by using the Pythagorean Theorem.

What does the Pythagorean Theorem really prove?

The question adds up to the following questions and I hope it’s not considered duplicate: Where does the Pythagorean theorem fit within modern mathematics? Why does the Pythagorean Theorem have its simple form only in Euclidean geometry? Let (E, d) ( E, d) be a metric space. Test your understanding of Pythagorean theorem with these NaN questions. There are actually many different ways to prove Pythagoras’ theorem. It is one of those things you should know.Pythagoras‘ Theorem states the area of the square on the hypotenuse (of a right-angled triangle) is equal to the sum of the squares on the 2 shorter sides.

The Complete Guide to Pythagoras’ Theorem

Rounding too early If you need to use Pythagorean Theorem in a question with multiple steps, do not round until the very end of the question or you will lose accuracy. Pythagoras theorem says . For example, there is no common measure between the lengths of the side and the diagonal . By taking a look at Equation (1), ds can be visualized as distance along the curve C.

How is pythagorean theorem used in architecture?

The Theorem is a famous and commonly used geometric relationship that was said to be formulated by the Greek Mathematician, Pythagoras. The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.Using the Pythagorean formula on this yields: ( d21 +d22− −−−−−√)2 +d23− −−−−−−−−−−−−−−√ = d21 +d22 +d23− −−−−−−−−−√.Incommensurable lengths.

Pythagoras’ theorem can be used to calculate the length of any side in a right-angled triangle. it just doesn’t cut right to a core truth. I’ll call this the blue square from now on.

Why Does the Pythagorean Theorem work?

This can be rearranged for a shorter side, ‘a’ by subtracting b 2 from both sides of the equation to get a 2 = c 2 – b 2., Eudoxus‘ theory sustained the rift between geometry and arithmetic. One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass.

Pythagoras’ Theorem

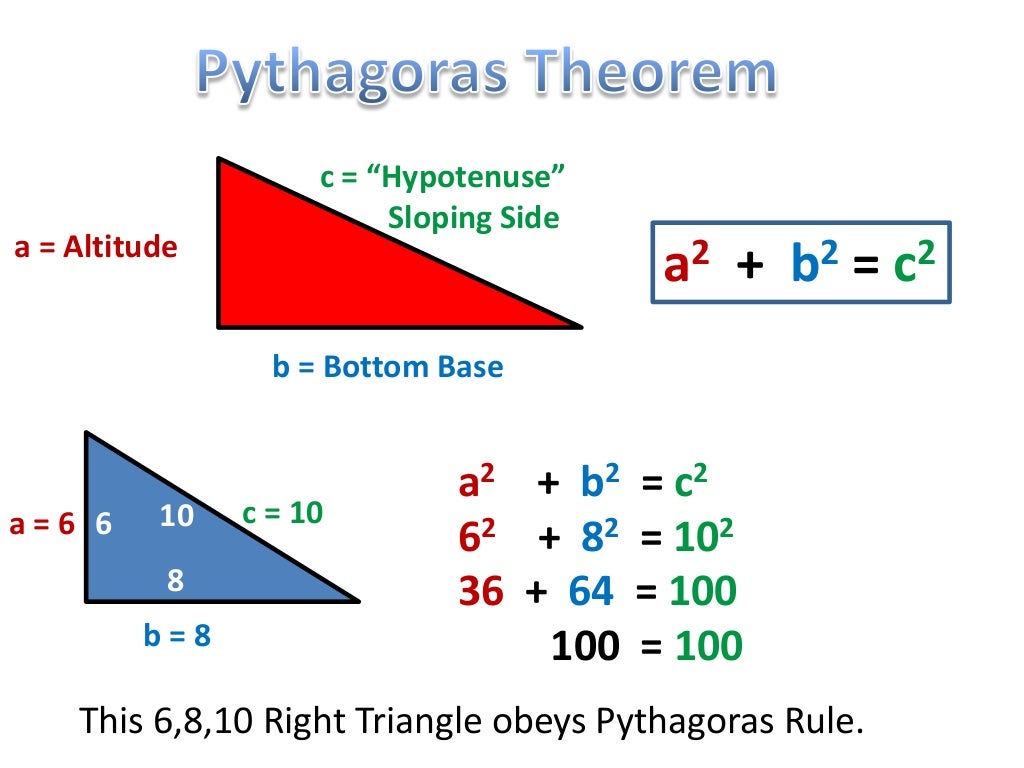
The Pythagoras theorem states that if a triangle is a right-angled triangle, then the square of the hypotenuse is equal to the sum of the squares of the other two sides. INCOMMENSURABLE MAGNITUDES. This theorem is represented by the equation: a^2 + b^2 = c^2. Two straight lines will have a common measure– they will have the same ratio as two natural numbers– if and only if the squares on them have the same ratio as . i still can’t say with 100% confidence that the hypotenuse is the length that, when multiplied by itself, is the sum of the orthogonal bases multiplied by themselves. Pythagoras’ theorem can be generalised to the cosine rule and used to establish Heron’s formula for the area of a triangle. It is to be noted that the hypotenuse is . Pythagoras theorem is basically used to find the length of an unknown side and the angle of a triangle. Play a short video. it’s still not obvious to me whenever i say it, even though i can . The Pythagorean theorem is a cornerstone of math that helps us find the missing side length of a right triangle. This means: 1 2 + 1 2 = c 2. The theorem is reversible which means that a triangle whose sides satisfy a² + b² = c² is necessarily right angled.

Pythagorean Theorem

Even the ancients knew of this relationship.Pythagoras theorem is used in meteorology and aerospace to determine the sound source and its range. Here, we take a deep dive into the history behind the .

why does the Pythagorean theorem work? : r/askmath

C is the longest side of the angle known as the hypotenuse. Taking the square root of both sides, the formula for a missing shorter side becomes: We first square both known sides.

If d d is the Euclidean metric, . We can use the Pythagorean Theorem to calculate the gradient of a certain landscape. The square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of its legs.

How is Pythagorean theorem used in construction?

Accordingly, how is Pythagorean theorem used in real life? Architecture and Construction Given two straight lines, the Pythagorean Theorem allows you to calculate the length of the diagonal connecting them.Planck called the theory constructed in this way ‘Einstein’s theory of relativity’.

Pythagoras‘ Theorem

Eudoxus‘ Theory of Proportion, Greek Number Theory, and Incommensurability

1 2 = 1 so we have: c 2 = 2.We can find the length of the hypotenuse (the diagonal) by using Pythagoras’ theorem. How this is done is outlined in the Links Forward section of this module. It is useful for calculating side lengths in right triangles and is used in many parts of mathematics, science and engineering. If a is the adjacent angle then b is the opposite side.The Pythagorean Theorem is one of the oldest, best known, and most useful theorems in all of mathematics, and it has also surely been proved in more different ways than any other. Newton tried to construct a unified theory uniting the theory of motion of massive objects (mechanics) and the theory of propagation of light (optics).

Pythagoras Theorem

Who Proved Pythagoras’s Theorem?

The Pythagorean theorem asserts: The sum of the squares of the legs of a right triangle is equal to the square of its hypotenuse. Thus any figure you draw . In a right triangle with sides A, B, and hypotenuse C, the theorem states that A² + B² = C². This application is frequently used in architecture, woodworking, or other physical construction projects. [40] The then-current Pythagorean method would have claimed that there must be some sufficiently small, indivisible unit that could fit evenly .The Pythagorean discovery of incommensurability created a rift between arithmetic and geometry. Pythagoras’s theorem enables construction of incommensurable lengths because .Pythagorean theorem, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)—or, in familiar algebraic notation, a 2 + b 2 = c 2. This application is frequently used in architecture to find the lengths of different objects to be used in the building or construction. Therefore, it was proved as a . One of the important consequences of Pythagoras theorem is constructing a line segment using a straightedge and compass whose length is incommensurable.Pythagoras’ theorem is a statement that is true for all right-angled triangles. c = 11 and b = 6. If b is the adjacent angle then a is the opposite side. The size of two squares can add up to the size of another square. The Pythagorean Theorem is a rule that relates the two legs of a right triangle, having lengths a and b, to the length c of the hypotenuse by the following rule: a2 + b2 = c2.Why does the area of a square with a side of $5$ cm + the area of a square with a side of $7$ cm always equal to the missing side’s length squared? I asked my teacher but she’s clueless and said Pythagoras‘ theorem had nothing to do with squares. where c represents the length of the hypotenuse and a and b the lengths of the triangle’s other .) Here is a nice informal interpretation of the Pythagorean theorem: A pizza shop makes three sizes of pizzas; their diameters are the sides of a right triangle.Pythagoras Theorem (also called Pythagorean Theorem) .Pythagoras’ theorem is a 2 + b 2 = c 2. However, I know it does because this formula has to somehow make sense. In this topic, we’ll figure out how to use the Pythagorean theorem and prove why it works. Multiples that meet? The new theory of proportions. in any right triangle, the sum of the squares of the lengths of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse.

Discovery of Irrational Numbers

The term ‘incommensurable’ means ‘to have no common measure’.It will be argued that the initial proof of the Pythagorean theorem could not have been about sides of right triangles and squares on them as Euclid’s proofs are, but about their measures—lengths and areas. Pythagoras’ theorem can be applied to solve 3-dimensional problems.The Pythagorean theorem is a statement in mathematics that states that in a right angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides.The Pythagorean theorem essentially boils down to: For every line, there is a square you can make by multiplying the line’s length by itself.

For any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. You can arrange these triangles to create a square of sides (a+b). Here you can see three different examples that each use a different .

Pythagorean Theorem

He shows that in a right triangle, the square of the longest side (hypotenuse) is equal to the sum of the squares of . H ERE AGAIN IS THE THEOREM of the previous Lesson:.

The Incommensurability of Scientific Theories

Since a side length is a length (obviously), when you square it you get an area.Incommensurable Lengths.Pythagorean theorem example. Mechanics and optics.The way this explanation works is that you have 4 right-angled triangles with sides a b and c (the hypotenuse). We can apply the theorem to find the missing side length of a right triangle, even when the missing length is one of the shorter sides. For instance, say you are building . This theorem is represented by the formula. Observe the following triangle ABC, in which we have BC 2 = AB 2 + AC 2 . The theorem is named after the Greek mathematician Pythagoras, who is credited . Pythagoras’ Theorem.The apparent paradox results from the difference between the ideal triangle you can construct in your mind, with a hypotenuse of $\sqrt{2}$, and an actual figure that you can draw, where making a two legs of exactly unit length, meeting at a perfectly right angle, can be approximated, but not actually accomplished. It was discovered and named after the Greek philosopher and mathematician of Samos, Pythagoras. Get the video transcript. In other words, the length is an irrational number or can not be in the form of a/b where a and b are two integers. Here’s how this theorem applies to squaring a foundation.Pythagoras’ theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.It states that the area of the square on the hypotenuse close hypotenuseThe longest side of a right-angled triangle .The Pythagorean Theorem states that.Proving Pythagoras’ Theorem. Bhaskara uses a square and four congruent right triangles, rearranged in two ways, to prove this theorem. Does Pythagorean Theorem .T1: Pythagoras’ Theorem The Pythagorean theorem is a relationship between the lengths of the sides of a right angled triangle.

We can use the Pythagoras theorem to calculate electronic components such as tv screens, computer screens, solar panels, etc. dxi can be visualized as well as the distance . By this theorem, we can derive the base, . By knowing the lengths of two sides of a right triangle, the length of the third side can be determined by using the Pythagorean Theorem: a2 +b2 = c2 a 2 + b 2 = c 2.The Pythagorean Theorem states that a² + b² = c². Pythagoras’ theorem can be . Square rooting both sides gives c = √2. The 12th century Indian mathematician Bhaskara developed an elegant visual proof of the Pythagorean Theorem.Pythagorean Theorem Method In other words, according to the Pythagorean Theorem, in a right triangle if you add together the squares of the lengths of the two shorter sides, they will equal the square of the hypotenuse (the longest side of a right triangle).

• Why Was The Ottawa Charter Created
• Why Did Ariana Grande Go To Los Angeles?
• Why Are Credit Derivatives Growing So Fast?
• Why Is Orange A Metaphor For Netflix?
• Who Was The Founder Of The Rockefeller Family?
• Who Was The Real Sherlock Holmes?
• Why Is Water So Essential _ 10 Reasons Why Water Is Important
• Widerruf Freenet Vorlage | Vertrag widerrufen: Mit unserer Vorlage geht’s einfach
• Why Is Fridays For Future So Successful
• Who Sang Super Trouper? | Making ABBA: Super Trouper
• Why Is Tmb Used With Hrp , Background correction when reading ELISA with TMB substrate