What Is Uniform Convergence? , Real Analysis 25

Di: Samuel

If we want to conclude uniform convergence N N shouldn’t be dependant on x x.Uniform convergence in probability is a form of convergence in probability in statistical asymptotic theory and probability theory. It is useful to consider the more general case.What you’re asked to show that almost uniform convergence does not imply the stronger uniform convergence almost everywhere. I am looking for a symbol that looks like two arrows of the same size, one on top of the other with (possibly) a letter on top, this is my paint sketch of it: I’ve tried something like. Determine whether the following functional series .

cauchy criterion for uniform convergence theorem - YouTube

Dominated convergence theorem.

Cauchy’s criterion for convergence

In order to make the distinction between pointwise and uniform convergence clearer, let us write down the relevant questions to ask in order to check whether one has pointwise or uniform convergence. Visual: The idea of uniform convergence is helped .Considering uniform convergence now, let’s first recall the definition of uniform convergence of a sequence of functions: |gn(x) − g(x)| < ϵ, for all n ≥ N and x ∈ I. In measure theory, Lebesgue 's dominated convergence theorem provides sufficient conditions under which almost everywhere convergence of a sequence of functions implies convergence in the L1 norm.1 suggests that we continue our discussion from sequences of real-valued functions to series of real-valued functions.

Uniform Convergence -- from Wolfram MathWorld

Uniform Convergence

Stack Exchange Network Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.Doubt on uniform convergence and sup-metric convergence. Visit Stack Exchange

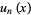
Uniform Convergence -- from Wolfram MathWorld

made with manim Communityvisit the homepage at https://www., pointwise convergence holds).

Pointwise and Uniform Convergence Visualized

The de nition of convergence The sequence xn converges to X when this holds: for any >0 there exists K such that jxn − Xj < for all n K.Uniform convergence in probability has applications to statistics as well . In the given example the author proves that for ϵ = 1 4 ϵ = 1 4 such N N doesn't exist.We've just been introduced to uniform convergence, and the method presented is to take the supremum of the absolute value of the difference between the limit function and the function in the sequen.一致收敛，或称均匀收敛，（英语： Uniform convergence ），是数学中关于函数序列收敛的一种定义。其概念大致可想成：若函数序列 f n 一致收敛至函数 f ，代表对所有定义域中的点 x ， f n (x) 收敛至 f(x) 会有（大致）相同的收敛速度。由于它对收敛要求较逐点收敛更强，故能保持一些重要的分析 . (The converse does not hold even for complete function spaces: for example, consider the harmonic series as a sequence of constant functions). Draw a picture to illustrate the above argument. ∥fn∥[a,+∞) = sup x∈[a,+∞) nx 1 +n2x2 ≤ sup x∈[a,+∞) nx 2n2x2 = sup x∈[a,+∞) 1 2nx ≤ 1 2na − →−−n→∞ 0.Let n ∈N be large enough so that 1 n 1 n or n2x2 > 1.

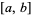
Uniform Convergence -- from Wolfram MathWorld

Each game actually is a translation of the corresponding definition. In mathematics, a uniformly bounded family of functions is a family of bounded functions that can all be bounded by the same constant. This is important because while a sequence of functions may converge pointwise, if it is converging at different rates at each point in may not converge uniformly.If the space is finite-dimensional, or it is a Hilbert space, the converse is also true: weak convergence+convergenc.Pointwise and Uniform Convergence 1.Support the channel on Steady: https://steadyhq. The method we used to deduce uniform convergence by comparing with a ‘known’ series of real numbers is very powerful and due to Weierstrass (it is a special .2 Uniform Convergence of Series.Look at this as a game between two people (practically, this can’t happen but let our imagination flow). Because $R$ is arbitrary, there is uniform convergence of $\{f_n\}_{n=1}^\infty$ on any bounded interval in $I$ and pointwise convergence at every point of $I$ since every point belongs to some bounded interval on which there is uniform convergence. Your best bet is to check the original . More intuitively all points on the {fn} are converging together to f. Uniform convergence of . The converse is also true, but the demonstration is not easy and was given by Weierstrass for the first time in 1880.

一致收敛

Uniform boundedness. One way to check is: if a series of continuous functions uniformly converges to a function, that limit will be .

Normal convergence

to the constant function f = 0 f . What is wrong with the following proof that seems to prove pointwise convergence implies uniform convergence? Hot Network Questions Serious device for making hummus at home Odds for second smallest prime factor Do creatures with a reach of 0 get attacks of opportunity . We say that a sequence ff

uniform convergence

Generalizations Local normal convergence The values of the functions need not be real numbers, but may be in any topological space, in order that the concept of pointwise convergence make sense.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site

Contents Uniform convergence

This constant is larger than or equal to the absolute value of any value of any of the functions in the family. This view is often . This N N should work for all x ∈ [0, 1] x ∈ [ 0, 1].Uniform convergence of the series on unbounded domain.Uniform convergence in integrated survival function implies uniform convergence of distribution functions? 1 Graphical Interpretation of Pointwise and Uniform Convergence of Functional Sequence

Uniform Convergence and Differentiability

Mathematical Deﬁnitions A power series, f(x) = X ∞ n=0 anx n, is an example of a sum over a series of functions f(x) = X∞ n=0 gn(x), (1) where gn(x) = anxn. However, since sup x |gUniform absolute-convergence is independent of the ordering of a series.Convergence is a term mathematically most common in the study of series and sequences.

Uniform convergence, and how to show it?

However the author explicitly states that x0 = 1 2√N x 0 = 1 2 N is a point at which the conclusion is wrong.

Uniform convergence

But I found new arguments: For any z z, find . For instance, as we have seen in the preceding example, the pointwise limit of a sequence of continuous functions is not necessarily continuous.The reader should note how this proof is a mix of the theory of series of real numbers (using in this case the convergence of ∑1∕n 2) and results on uniform convergence. so fn → 0 uniformly on [a, +∞). If there is a convergent series of constants sum_ (n=1)^inftyM_n, such that |u_n (x)|<=M_n for all x in E, then the series exhibits absolute convergence for each x in E as well as uniform convergence in E.

Real Analysis 25

A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE 5 Exercise 2.uniform convergence. • If g n(x) = x(1+1/n) and g(x) = x, then obviously g n(x) → g(x) for all x (i. With pointwise convergence each x has its own N for each ǫ. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over . I usually did this by showing that on every |z| < N | z | < N the convergence is uniform, so that f(z) f ( z) converges uniformly on every compact subset of C C, hence f(z) f ( z) is entire. This is because, for a series of nonnegative functions, uniform convergence is equivalent to the property that, for any ε > 0, there are finitely many terms of the series such that excluding these terms results in a series with total sum less than the constant function ε .均勻收斂，或稱一致收斂，（英語： Uniform convergence ），是數學中關於函數序列收斂的一種定義。其概念大致可想成：若函數序列 f n 均勻收斂至函數 f ，代表對所有定義域中的點 x ， f n (x) 收斂至 f(x) 會有（大致）相同的收斂速度。由於它對收斂要求較逐點收斂更強，故能保持一些重要的分析 .To quote Bottazzini again: “The uniform convergence of a series in an interval as defined by ($U_1$) naturally implies uniform convergence in the neighbourhood of every point in the interval.com/en/brightsideofmathsOr support me via PayPal: https://paypal. (1) (1) | g n ( x) − g ( x) | < ϵ, for all n ≥ N and x ∈ I. UNIFORM CONVERGENCE Uniform convergence is the main theme of this chapter. (1) and ask whether the sum is convergent.

Uniform convergence in probability

Uniform Convergence Implies

Let sum_ (n=1)^ (infty)u_n (x) be a series of functions all defined for a set E of values of x. I’ve seen this symbol used to say that a sequence of functions . On the other hand, for [0, +∞) we have.Uniform convergence, in analysis, property involving the convergence of a sequence of continuous functions—f1(x), f2(x), f3(x),. Cauchy Criterion for Uniform Convergence of Series. While the mathematical contributions of these individuals to the concept of uniform convergence have been much discussed, Weierstrass is considered to be the actual inventor of today’s concept.?⏩Comment Below If This Video Helped You ?Like ? & Share With Your Classmates – ALL THE BEST ?Do Visit My Second Channel – https://bit.The history of uniform convergence is typically focused on the contributions of Cauchy, Seidel, Stokes, and Björling. Given a complex function f(z) = ∑fn(z) f ( z) = ∑ f n ( z), I want to show that f(z) f ( z) is entire.uniform convergence is equivalent to convergence using the supremum norm. Proving uniform convergence on an unbounded interval.ly/3rMGcSAThis vi.Pointwise convergence is a very weak kind of convergence.Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Topology of uniform convergence

me/brightmathsOr via Ko-fi: https://ko-fi. Show uniform convergence of a function series.

Weierstrass M-Test

1 It is easy to demonstrate that uniform convergence is not the same thing as point-wise convergence by exhibiting examples in which pointwise convergence holds but uniform convergence does not. Uniform convergence means that you have a uniform control over the speed of convergence of fn(x) f n ( x) as n → ∞ n → ∞ for different values of x x ’s. Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals. Informally, this says that as n gets larger and larger the numbers xn get closer and closer to X. \xrightarrow{\xrightarrow{n}} and similar combinations but it always makes one arrow smaller. Lets make a game for it.Butthe de nition is something you can work with precisely. Extension of uniform convergence to the end point points : Series of continuous functions. Note that (1) ( 1) must hold for each n ≥ N n ≥ N and every x ∈ I x ∈ I. A model is said to converge when the series s(n) = losswn(y^, y) s ( n) = l o s s w n ( y ^, y) (Where wn w n is the set of weights after the n n ‚th iteration of back-propagation and s(n) s ( n) is the n n ‚th term of the series) is a converging series. If we consider each x .This could be a theorem that states that uniform convergence implies pointwise convergence, which is a true theorem, but ONLY in this direction, so it cannot say if and only if.Uniform convergence, on the other hand, does not make sense for functions . In Section 1 pointwise and uniform convergence of sequences of functions are discussed and examples are given.Cauchy’s criterion for convergence 1. (It does have something .Normal convergence implies norm-topology convergence if and only if the space of functions under consideration is complete with respect to the uniform norm. You want to prove pointwise convergence. The notion of uniform convergence is a stronger type of convergence that remedies this de ciency. Recall that the formal sum ∑ k = 1 ∞ f k is called a series of functions.

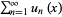
Uniform Convergence -- from Wolfram MathWorld

In Section 2 the three theorems on exchange of pointwise limits, inte-gration and di erentiation which are corner stones for all later . Uniform convergence of telescopic function series. Have a question about using Wolfram|Alpha? Contact Pro Premium Expert Support ». ∥fn∥[0,+∞ . This converges pointwise to the function 0 0 on (0, 1) ( 0, 1) and to 1 1 at 0 0, that is, it converges a.takes the value when is an integer and when is not an integer, and so is discontinuous at every integer.It means that, under certain conditions, the empirical frequencies of all events in a certain event-family converge to their theoretical probabilities. Let us consider a sum of the form given in eq. Series of Functions; Uniform Convergence. Uniform convergence of functions series.Calculus and Analysis.Uniform convergence of a specific sequence of functions. Discuss the convergence and the uniform convergence of a series. The topology on the space $ {\mathcal F} ( X, Y) $ of mappings from a set $ X $ into a uniform space $ Y $ generated by the uniform structure on $ {\mathcal F} ( X, Y) $, the base for the entourages of which are the collections of all pairs $ ( f, g) \in {\mathcal F} ( X, Y) \times {\mathcal F} ( X, Y) $ such .In particular, it must converge uniformly (and pointwise) on that interval.Topology of uniform convergence. In particular, for any positive number ε > 0 there .Uniform convergence is concerned with ALL points in the domain at the SAME time.community/Custom Intro music by Saint Jean, check him out!Saint Jean – https://www.

Why is $f

Note 2: The critical diﬀerence between pointwise and uniform convergence is that with uniform con-vergence, given an ǫ, then N cutoﬀ works for all x ∈ D. A simple example for this is the sequence fn =xn f n = x n on [0, 1] [ 0, 1]. Consider a sequence of functions { f n ( x )} defined on a set E. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, .一致收敛是高等数学中的一个重要概念，又称均匀收敛。一致收敛是一个区间（或点集）相联系，而不是与某单独的点相联系。除了柯西准则和余项准则外，还可以通过Weierstrass判别法、Abel判别法和Dirichlet判别法来判别函数项级数是否一致收敛。—to a function f(x) for all x in some interval (a, b).

BAHTMZ

General