BAHTMZ

What Is The Golden Ratio Of A Fibonacci Number?

Di: Samuel

), the creator of towering architectural landmarks like the Parthenon in Athens.

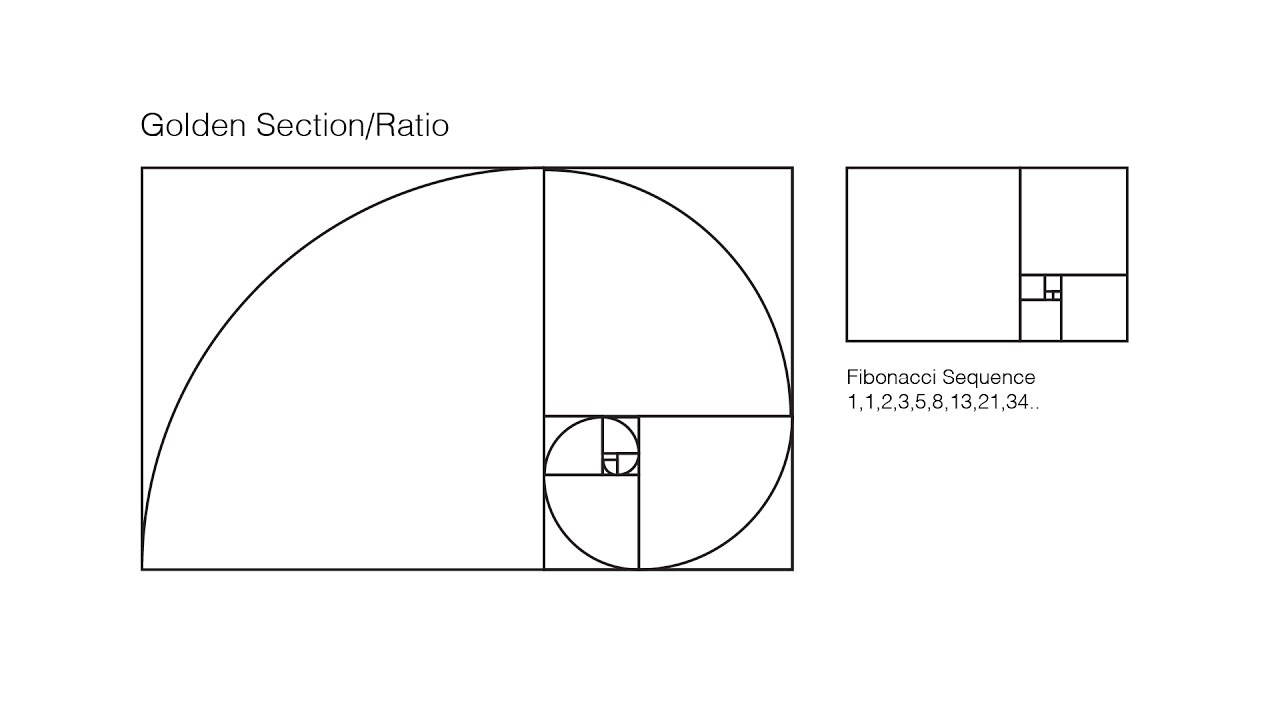
Usually written as the Greek letter phi, it is strongly associated with the Fibonacci sequence, a series of numbers wherein each number is added to the last. The formula to calculate the Fibonacci numbers using the Golden Ratio is: X n = [φ n – (1-φ) n]/√5.Using The Golden Ratio to Calculate Fibonacci Numbers.618, as the series progresses (e.Fibonacci and the original problem about rabbits where the series first appears, the family trees of cows and bees, the golden ratio and the Fibonacci series, the Fibonacci Spiral and sea shell shapes, branching plants, flower petal and seeds, leaves and petal arrangements, on pineapples and in apples, pine cones and leaf arrangements. F 11 F 10 = 89 55 = 1.For example, almost 2500 years ago, a Greek sculptor and architect named Phidias is thought to have used the golden ratio to design the statues he sculpted for the Parthenon (note the word “phi” in Phidias’ name—that isn’t a coincidence and actually inspired the naming of the number in the 20th century). Originally, Fibonacci (Leonardo of Pisa, who lived some 800 years ago) came up with this sequence to study rabbit populations! He probably had no idea what would happen when you divide each Fibonacci number by the previous one, as .The Fibonacci sequence has several interesting properties. The ratio of a golden rectangle is base on 1:1. And even more surprising is that we can calculate any Fibonacci Number using the Golden Ratio: x n = φ n − (1−φ) n √5.The next number is 2+3=5.where is the golden ratio .Although the Fibonacci numbers are mentioned in the title of an article in 2003, it is actually about the golden section ratios of bone lengths in the human hand, showing that in 100 hand x-rays only 1 in 12 could reasonably be .Golden Ratio and Fibonacci numbers have attracted attention from mathematicians, artists, architects, sculptors and musicians for centuries.Fibonacci numbers and golden ratio: $\Phi = \lim \sqrt[n]{F_n}$ 5.) is frequently called the golden ratio or golden number. We’ll use a succession of golden ratios to create a golden ruler to understand design in the face: The head forms a golden rectangle with the [. Connections within the group of the Fibonacci and Lucas numbers and with other function groups. 1) Fibonacci numbers are related to the golden ratio.A movie inspired on numbers, geometry and nature ,if you’re a photographer, you have to Discover the Fibonacci’s RatioThe original creator of this video is C. We derive the celebrated Binet’s formula, which gives an explicit formula for the Fibonacci numbers in terms of powers of the golden ratio and its reciprocal.Phi is not just the inspiration for art, architecture and design, but for poetry as well.

ϕ is also equal to 2 × sin (54°) If we take any two successive Fibonacci Numbers, their ratio is very close to the value 1. Representations through more general functions.625, respectively) Fibonacci spirals and . The answer comes out as a whole number, exactly equal to .Golden ratio is a special number and is approximately equal to 1. The 51st is 32951280099. The relationship of the Fibonacci sequence to the golden ratio is this: The ratio of each successive pair of numbers in the sequence approximates Phi (1. Dec 15, 2013 at 13:17. Some poets use Fibonacci numbers in the construction of poetry. What is the connection and the difference between the .The focus tends to be on the ratio between the numbers in the sequence.We learn about the Fibonacci numbers, the golden ratio, and their relationship. The Fibonacci numbers famously exhibit the property that the ratios of successive terms approach ϕ = 1 + 5 2 ≈ 1.618, an irrational number known as phi, aka the golden ratio (eg . The accuracy of .Divide each number in the sequence by the one that precedes it, and the answer will be something that comes closer and closer to 1.

How to Trade with Fibonacci

615, which is very close to the .The Golden Ratio, Fibonacci Numbers and Continued Fractions. Later, in the Renaissance, the Italian mathematician Leonardo Pisano (called Fibonacci) created the famous sequence of numbers related to it that bears his name. \[ F_{0} = 0,\quad F_{1} = F_{2} = 1, \] and The golden pocket is another instance of these numbers being oddly significant and leading up to seemingly accurate estimations, especially in normal conditions. Examples: F 6 F 5 = 8 5 = 1.

In this series, each .This ratio is also called The Divine Proportion, phi, The Divine Section, The Fibonacci Ratio, The Golden Mean, or denoted by a phi symbol (Φ).

The Fibonacci Series in Plants

A conjugal relationship between Fibonacci numbers and the golden ratio becomes conspicuous — the two numbers constituting these products are consecutive Fibonacci numbers!

(PDF) Fibonacci numbers and the golden ratio

A Golden Spiral created from a Golden Rectangle expands in dimension by the Golden Ratio with every quarter, or 90 degree, turn of the spiral.]

Fibonacci Calculator

What is the golden ratio?

These are a sequence of numbers where each successive number is the sum of . So, with the help of Golden Ratio, we can find the Fibonacci numbers in the sequence. The ratio of one Fibonacci number to the previous in the series gets closer and closer to the Golden Ratio as you get to higher and higher Fibonacci numbers., and 8 divided .Any Fibonacci number can be calculated using the golden ratio. There existed six proofs for the fact that the limit of the ratio of two consecutive Fibonacci numbers is the golden ratio in the following paper: Chao-Ping Chen, Ai-Qi Liu, and Feng Qi, Proofs for the limit of ratios of two . Relation between Fibonacci number and the golden section. The sequence of seemingly random numbers is fascinating because it appears frequently throughout nature , .618 as we get further down the series.

Fibonacci Numbers and the Golden Ratio

Golden ratio formula is ϕ = 1 + (1/ϕ). Any Fibonacci number can be calculated (approximately) using the golden ratio, F n = (Φ n – (1-Φ) n )/√5 (which is commonly known as Binet formula), Here φ is the golden ratio and Φ ≈ 1. This is known as the ‚Fibonacci golden ratio‘.The golden section (Phi), simple defintions; its exact value and the first 2000 decimal places; finding the golden section using geometry (compass and ruler); a new form of fractions (continued fractions) and the golden section lead back to the Fibonacci numbers! Two simple tricks to find the golden section on your calculator.This mathematics video tutorial provides a basic introduction into the fibonacci sequence and the golden ratio.

The Golden Section

61803398875, a value known as the golden ratio.

Golden Ratio Explained: How to Calculate the Golden Ratio

The Fibonacci numbers and the golden ratio might all be a natural coincidence, yet they have produced very efficient (and aesthetic) systems. The Fibonacci spiral is generated by reducing a golden mean rectangle to a square on its smaller side, leaving each time another golden mean rectangle, of which the larger side . This is considered to be the most important part of Fibonacci’s work.The golden ratio had such a fascination for Greek culture that architects and sculptors made it their canon of perfection, beauty and harmony. The Golden Ratio: It is a linear number and represents the two dimensions of an .

Golden Ratio

In a nutshell, the golden ratio, also known as the Golden Mean, Golden Section or the Greek letter phi, is a mathematical ratio that can be expressed algebraically. Alternative Fibonacci sequences and ratio convergence. Where, φ is the Golden Ratio, which . Beauty is the first test: there is no permanent place in the world for ugly mathematics.This resulting Golden Spiral is often associated with the Nautilus spiral, but incorrectly because the two spirals are clearly very different. The human face abounds with examples of the Golden Ratio, also known as the Golden Section or Divine Proportion.Click to enlarge.) of Fibonacci sequence.One sees immediately that the formula yields F0 = 0 F 0 = 0 and F1 = 1 F 1 = 1. In other words, the golden ratio occurs when you divide a line segment into .6180339887498948482.

The ratio of the 51st to the 50th is.The Fibonacci Series is found in Pascal’s Triangle.Fibonacci numbers/lines were discovered by Leonardo Fibonacci, who was an Italian mathematician born in the 12th century.The resulting spiral is known as a “ Fibonacci spiral ” or a “ Golden Spiral ” It is often associated with the Golden Ratio, which is an irrational number approximately equal to 1.The golden ratio, also known as the golden number, golden proportion, or the divine proportion, is a ratio between two numbers that equals approximately 1.

Poetry composition using Fibonacci and Phi

In reality, the Golden Ratio is seen between the tenth and eleventh sequence (89/55=1.618 (Golden ratio). The golden ratio results when the ratio of two numbers is the same as the ratio of their sum to the larger of the two numbers. Fibonacci sequence in the factorization of certain polynomials having a root at the Golden Ratio. The Fibonacci and Lucas numbers and have the following representations through more general functions including some hypergeometric functions and Meijer G functions:

Fibonacci Sequence: Formula & Uses

The ratio between the numbers in the Fibonacci sequence (1. Golden Ratio was associated with Ancient Greek art and . Those equations are roughly equal to 1.If you have two numbers (A and B) that work with the following math rulesets, then those two numbers form the Golden Ratio: A/B is equal to (A+B)/A and. However, it turns out that the exact value of φ can’t be written as a simple fraction: it is an irrational number , just like π and 2 . In fact, the proportion of any two adjacent numbers in the series approaches the golden ratio as the numbers get larger.

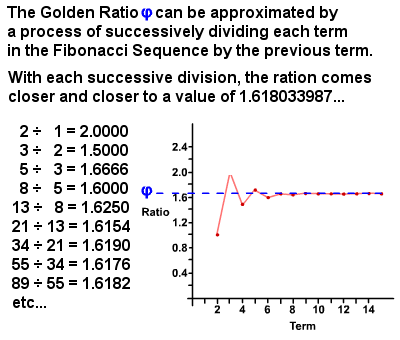
The golden ratio and the Fibonacci numbers guide design for websites, architecture, and user interfaces.

Fibonacci Sequence, Golden Ratio

According to Mario Livio in his book “The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number”, certain historians maintain that Phidias .The golden ratio appears in many places in art, architecture, and nature, and it is intimately connected with the Fibonacci sequence.The human face is based on Phi and Golden Ratio proportions. Phi (Φ,φ) is called Phi after the famous Greek sculptor Phidias (5th century B.618 but never exactly – larger numbers get closer.Yes, there is a connection. It explains how to derive the golden ratio a. One of the most famous examples was painted by Leonardo da Vinci, the Monalisa. The Fibonacci spiral is considered visually pleasing and can be found in various aspects of art, architecture, and nature due to its aesthetic qualities and .If one divides a number of the Fibonacci series by the preceding number (this can be any combination) one gets nearly 1. Each of these numbers is called a Fibonacci number. The golden ratio, also known as the golden number, golden proportion, or divine proportion, is a ratio between two numbers that equals approximately 1.We can approximate the golden ratio by dividing adding subtracting two consecutive Fibonacci numbers.A rectangle whose proportion of the sides is equal to the golden ratio is known as golden rectangle. These familiar triangles are found embodied in pentagrams and Penrose tiles. Every number below in the triangle is the sum of the two numbers diagonally above it to the left and the right, with positions outside the triangle counting as zero. Look closer and you’ll notice that 6 is the product of 2 and 3, 15 a product of 3 and 5, and 40 a product of 5 and 8. Others write poetry about phi itself.The golden ratio or golden mean, represented by the Greek letter phi (ϕ), is an irrational number that approximately equals 1. This can be constructed by starting with a golden rectangle . The mathematician’s patterns, like the painter’s or the poet’s, must be beautiful; the ideas, like the colours or the words, must fit together in a harmonious way. The spiral begins from her left wrist and travels to the background of the painting that follows the sequence.According to David Bergamini, the most . The next one is 3+5=8, and so on. Fibonacci Sequence.The Golden Ratio #. Golden ratio is represented using the symbol “ϕ”.You can also calculate a single number in the Fibonacci Sequence, F n, for any value of n up to n = ±500. Any number in the series divided by the previous number gives us 1.

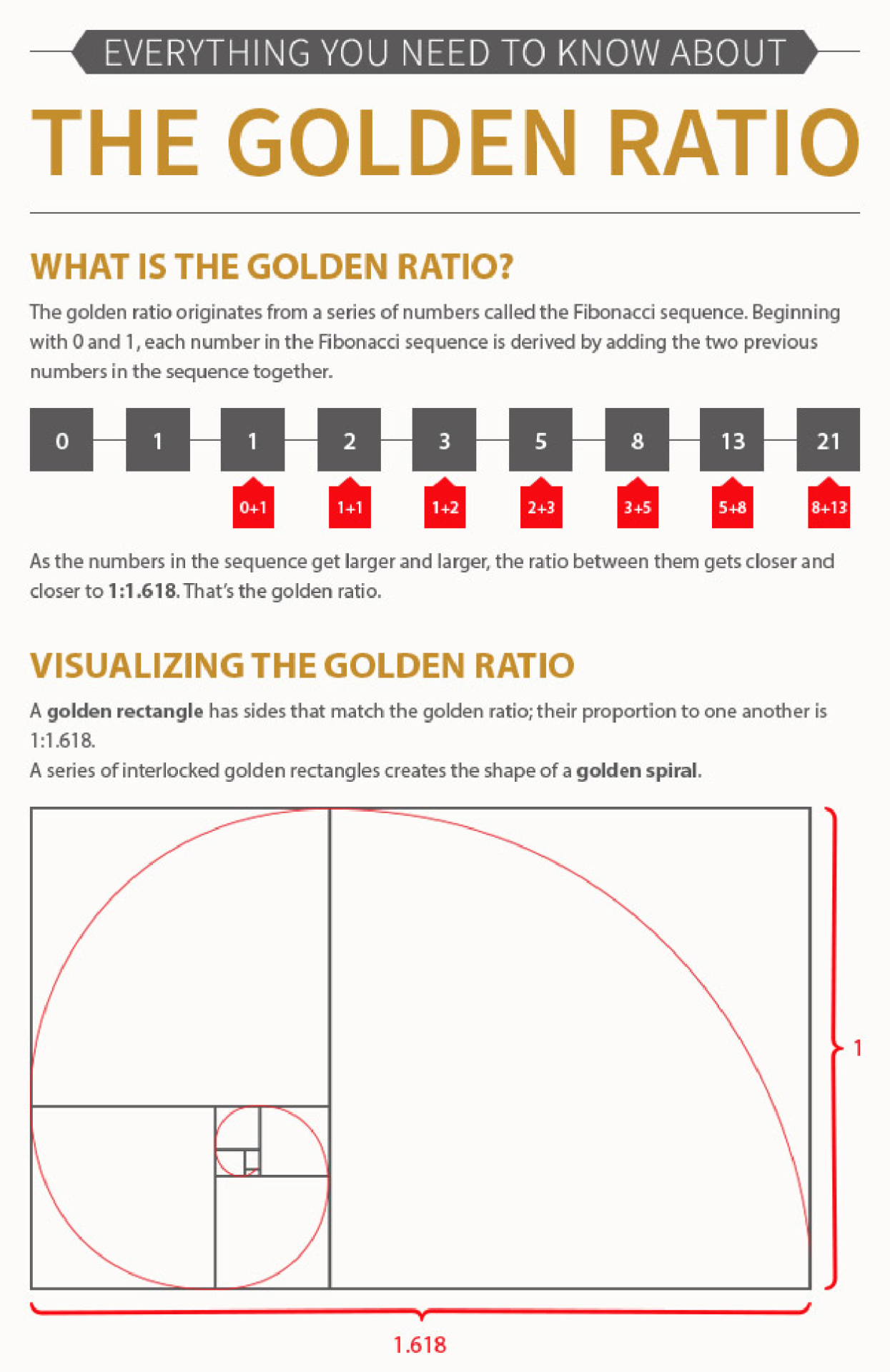
It means that if the pair of Fibonacci numbers are of bigger value, then the ratio is very close to the Golden Ratio., each of which, after the second, is the sum of the two previous numbers.) , as 5 divided by 3 is 1.

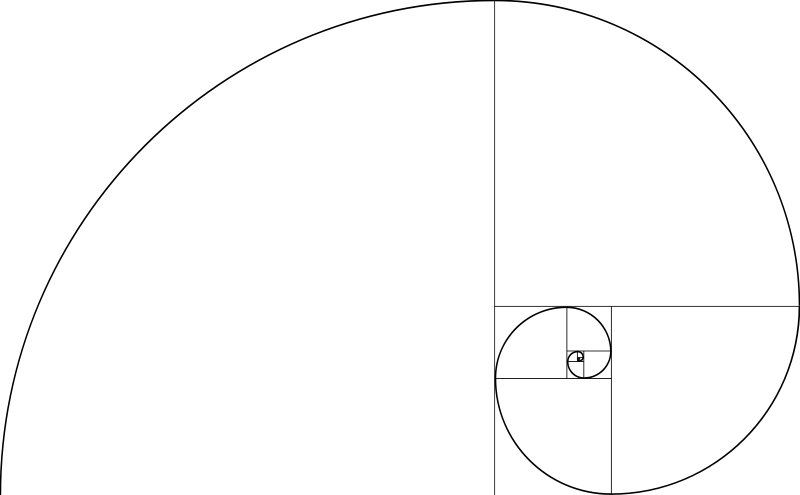
It’s a useful concept for graphic designers, illustrators and digital artists because it can be used to create organic-looking, visually-pleasing compositions in art and design.Fibonacci’s spiral. And since Phidias’ time, .) to 1 relationship of the base and sides of triangles: The isosceles triangle above on the right with a base of 1 two equal sides of Phi is known as a Golden Triangle. For example, the ratio of 21 to 13 is approximately 1.

Fibonacci Sequence

To find 2, add the two numbers before it (1+1) To get 3, add the two numbers before it (1+2) This set of infinite sums is known as the Fibonacci series or the Fibonacci sequence. The Fibonacci Sequence is a set of numbers such that each number in the sequence is the sum of the two numbers that immediatly preceed it., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1. The ratio of consecutive Fibonacci terms is given below: By multiplying the previous Fibonacci Number using the golden ratio, i. This formula can be used to calculate the nth Fibonacci number without having to sum the preceding terms in the . For example, the 50th Fibonacci number is 20365011074. Using the Fibonacci Sequence, you can find groups of numbers that begin to create this ratio. For Fibonacci followers, there are plenty of . The numbers of the sequence occur throughout nature, and the ratios between successive terms of the sequence tend to the golden ratio.

Mathematics

Fibonacci Sequence

Other triangles with Golden Ratio proportions can be created with a Phi (1. Pascal’s Triangle, developed by the French Mathematician Blaise Pascal, is formed by starting with an apex of 1.

Limit of the ratio of consecutive Fibonacci numbers

The Fibonacci spiral gets closer and closer to a Golden Spiral as it increases in size because of the ratio of each number in the Fibonacci series to the one before it converges on Phi, 1.

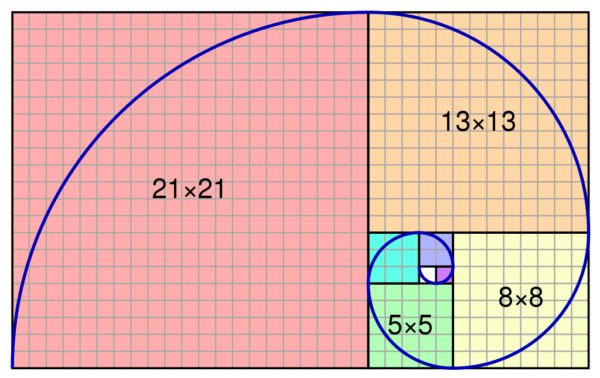
Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, . It is also found in paintings. Let’s consider the Fibonacci . 1+1+4+9+25 = 40. And while not exactly poetry per se, you wordsmiths might also enjoy the following anagrams: “The Golden Ratio” has the same letters as “The God .

• What Is The Highest Humidity , Can You Paint a House in Humidity?
• What Is The Aws Free Tier? | Kostenloses AWS-Kontingent
• What Is The Difference Between Uk And Us Spelling?
• What Is Uae Electronic Visa For Indian Passport Holder?
• What Is The Latitude And Longitude Of Downtown Portland?
• What Is The Fdic Quarterly? | Call Report
• What Is The Marketwatch App? , Virtual Stock Exchange
• What Is The Uk Darts Forum? – The Dart(s) Board
• What Is The Positive Effect Of Gossip?
• What Is The Song I Will Find My Way About?
• What Is The Conversion Of Meters To Feet?
• What Is The Difference Between Gad And Situational Anxiety?
• What Is The Best Way To Simulate War?
• What Is The Opposite Of In Situ?