BAHTMZ

General

What Is Rearranging Bernoulli’S Equation?

Di: Samuel

Hence, it is important to understand the underlying assumptions in order to apply it accurately in fluid flow analysis. P1 + 1 2ρv21 = P2 + 1 2ρv22. m2 _1A1V1= _2 A2V2 For incompressible flow A1V1= A2V2 Assume steady flow, V parallel to streamlines & no viscosity.Thus, Bernoulli’s equation states that the total head of the fluid is constant. This means that the equation assumes the absence of viscous forces or any form of .8 meters per second squared.The equation relating fluid pressure, kinetic energy, and potential energy from state to state is known as the Bernoulli equation, and is as follows: P1 + 1 2ρv21 + ρgh1 = P2 + 1 2ρv22 + ρgh2.Bernoulli’s equation: P + 1 2ρv2 + ρgh = constant P + 1 2 ρ v 2 + ρ g h = constant. work done on a unit volume of uid by . The above equation is the Bernoulli’s equation. One of the key assumptions of the Bernoulli equation is that the flow is frictionless. Bernoulli’s principle states that higher .The Curiosity Stream and Nebula bundle is no longer available, but you can still sign up for Nebula and get acess to my bonus videos – use this link for 40% .Fluid Mechanics – Continuity Equation Bernoulli’s equation Y1 Y2 A1 V1 A2 V2 =. Situations in which fluid flows at a constant depth are so important that this equation is often called Bernoulli’s principle. The first restriction on Bernoulli’s equation is that no work is allowed to be done on or by the fluid.1} and there are many .

Bernoulli's Principle - GeeksforGeeks

The net work done is the result of a change in fluid’s kinetic energy and gravitational potential energy. It is important because it allows us to analyze and predict the behavior of fluids in various situations, such as in pipes, pumps, and airplanes.The Bernoulli differential equation is an equation of the form \(y’+ p(x) y=q(x) y^n\).Because Bernoulli’s equation relates pressure, fluid speed, and height, you can use this important physics equation to find the difference in fluid pressure between two points.Calculation of Bernoulli’s Equation. Application of Bernoulli’s Equation. In this figure, M(x,t) is the bending moment, Q(x,t) is the shear force, and f(x,t) is the external force per unit length acting on the beam.

Bernoulli's Equation and Unit Conversion Strategies - Unit 4C - PEMY ...

Bernoulli’s theorem is the principle of energy conservation for perfect fluids in steady, or streamline, flow and is the basis for many engineering applications. p1 + ρgh1 = p2 + ρgh2.

Bernoulli’s Theorem

All you need to know is the fluid’s speed and height at those two points. (blood) pressure = F/area = m*a/area = m*v / area*second.Bernoulli’s equation is typically written: P + 1 2ϱ v2 + ϱgh = constant.Bernoulli’s equation expresses conservation of energy for flowing fluids (specifically incompressible fluids), such as water.) In this case, we get. Daniel Bernoulli has deduced that with the flow speed increase, there is a decrease in pressure, but there was a slight change, concluded by Leonhard Euler, who has provided us with this usual form of Bernoulli equation in the . Rearranging the equation will yield.Bernoulli’s Principle. This is a non-linear differential equation that can be reduced to a linear one by a clever substitution. L’équation de Bernoulli s’écrit généralement de la manière suivante : P 1 + 1 2 ρ v 1 2 + ρ g h 1 = P 2 + 1 2 ρ v 2 2 + ρ g h 2. Bernoulli’s equation relates a moving fluid’s pressure, density, speed, and height from .The Bernoulli equation is one of the most famous fluid mechanics equations, and it can be used to solve many practical problems.Free equations calculator – solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps. When n = 0 the equation can be solved as a First Order Linear Differential Equation. CONNECTION: Bernoulli’s equation is a restatement of the principle of energy . For a streamlined fluid flow, the sum of the pressure (P), the kinetic energy per unit volume ρ ( ( ρ v) 2 2) and the potential energy per unit volume (ρgh) remain constant. p2 = p1 + ρgh1.

Bernoulli’s Equation

Bernoulli’s equation states that the overall sum of these energies doesn’t change along a streamline – the energy of the fluid is just transferring between these different forms. P 1 + 1 2 ρv 1 2 + ρ gh 1 = P 2 + 1 2 ρv 2 2 + ρ gh 2. It states P + {{1\over 2}}\rho v^2 + \rho gh = \hbox{[constant]}, where P is the static pressure (in Newtons per square .Extended Bernoulli’s Equation.

Bernoulli’s Principle: Equation, Derivation, Applications

Since density is a constant for a low speed problem, the equation at the bottom of the slide relates the pressure and velocity at station two to the conditions at station one. Although we derived Bernoulli’s equation in a relatively simple situation, it applies to the flow of any ideal fluid as long as points 1 and 2 are on the same streamline.The Bernoulli equation was one of the first differential equations to be . Bernoulli’s equation as stated in previously is. p 1 + ρ g h 1 = p 2 + ρ g h 2. The new equation is a first order linear differential equation, and can be solved explicitly. It is Bernoulli’s equation for fluids at constant depth. Applying work-energy theorem in the volume of the fluid, the equation will be.L’équation de Bernoulli relie les pressions, les vitesses et les altitudes de deux points d’une ligne de courant d’un fluide de masse volumique ρ en écoulement laminaire permanent.1) and there are many examples . Suppose this pipe undergoes a gradual expansion in diameter. In the real world energy isn’t completely . There are some conditions to use Bernoulli’s equation. This page titled 12. (Any height can be chosen for a reference height of zero, as is often done for other situations involving gravitational force, making all other heights relative. All these conditions are impossible to satisfy at . Mathematically:- P ρ ρ constant P + ρ v 2 2 + ρ g h = constant.A Bernoulli equation has this form: dy dx + P (x)y = Q (x)yn.3: The Most General Applications of Bernoulli’s .Ans: Bernoulli’s equation is applied to all problems of incompressible fluid flow.

3: Bernoulli Equation

Our potential energy is the same, so we can remove that part from the equation.Applying Bernoulli’s equation to our scenario, we write that ? one plus one-half ? ? one squared plus ?? times ℎ one is equal to ? two plus one-half ? ? two squared plus ?? ℎ two. For a moving fluid, the energy of the system can be broken down into two components which are measures of the amount of energy of the system at . Most students reading this will have a fairly extensive use of Eqn. This is a significant limitation, because most hydraulic systems (especially in nuclear engineering) . Bernoulli’s equation is used to solve any problems involving incompressible fluid flow.

What is Extended Bernoulli’s Equation

1) this area is the whole area meeting the blood inside the vessel. Type in any equation to get the solution, steps and graphBernoulli’s principle provides a relationship between the pressure of a flowing fluid to its elevation and its speed.It shows the equivalence of the overall energy for a given volume of a fluid as it moves. while the whole area of 1) stays still. However, the 1 and 2 of both the sides of the equation denotes two different points . This was first derived in 1738 by a Swiss mathematician, Daniel Bernoulli.Lateral vibration of beams is governed by well-known Bernoulli-Euler equation. where n is any Real Number but not 0 or 1. Bernoulli’s theory is used to study the unstable potential flow used in the theory of ocean surface waves and acoustics. There are two main assumptions, that were applied on the derivation of the simplified Bernoulli’s equation.C B is an arbitrary constant called Bernoulli’s constant or Bernoulli’s function. Other forms of energy include the distribution of thermal energy due to fluid viscosity. 2) which is different from the areas above (that is the dissected 2-d circle) 3) when dilation happens, the area of 2-d circle is growing.Under that condition, Bernoulli’s equation becomes.

Bernoulli Equation

We’ll treat ?, the acceleration due to gravity, as exactly 9.

Bernoulli's Equation Basic Example #Bernoulli's Equatio - YouTube

Finding flow rate from Bernoulli’s equation

Bernoulli’s law describes the behavior of a fluid under varying conditions of flow and height. • The equation relates the states at two points along a single streamline, (not conditions on two different streamlines). Bernoulli’s equation is an equation from fluid mechanics that describes the relationship between pressure, velocity, and height in an ideal, incompressible fluid. Khan Academy es una organización sin fines de lucro, con la misión de proveer una educación gratuita de clase mundial, para cualquier persona en cualquier lugar. 2 Bernoulli Equation – energy • Consider energy terms for steady flow: • We write terms for KE and PE at each point Y1 Y2 A1 V1 A2 V2 Ei = KEi + . Now let’s discover a sufficient condition for a nonlinear first order differential equation

Bernoulli’s Law

For other values of n we can solve it by substituting. We can further simplify the equation by setting h2 = 0. Learn how to derive Bernoulli’s equation by looking at the example of the flow of fluid through a pipe, using the law of conservation of .Bernoulli’s equation has some restrictions in its applicability, they are: • Flow is steady; • Density is constant (which also means the fluid is incompressible); • Friction losses are negligible. Conservation of energy is applied to the fluid flow to produce Bernoulli’s equation.

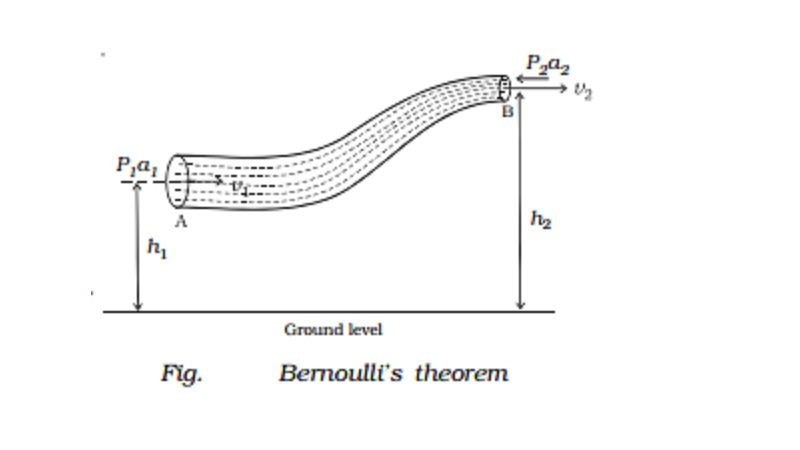
Bernoulli's theorem

The Bernoulli equation can also be expressed by saying that the constant in the equation is the same at the starting and ending point such that the three terms sum to the same value at these two points and as such can be set equal to each other.Bernoulli’s equation relates the pressure, flow speed, and height at two points in an ideal fluid. If the elevation of the fluid increases, for example, the pressure or the velocity must reduce in proportion. But often we neglect them.Rearranging the above equation, we get Bernoulli’s Equation – p 1 + ½ ρ v 1 2 + ρg y 1 = p 2 + ½ ρ v 2 2 + ρg y 2. Frictionless Flow. In that case, the continuity .Bernoulli equation, or the incompressible steady flow energy equation, is considered one of the most well-known equations in physics ( fluid mechanics) and it explains the conservation of mechanical work-energy. The equation was published in 1738 by Daniel Bernoulli (a Swiss physicist) to help us understand fluid flow.Bernoulli’s equation can be applied when syphoning fluid between two reservoirs. Bernoulli’s equation is an approximation and may sometimes include a term to describe the loss of energy from the system. It is one of the most important/useful equations in fluid mechanics. When n = 1 the equation can be solved using Separation of Variables. But we use this equation in many cases where the fluid is air, such as to find the lifting force on the wings of an airplane (image below), to . Dividing each term by ∆V, we will obtain the equation.Bernoulli’s equation has some restrictions in . Consider a pipe containing an ideal fluid. Both P 1 P 1 and P .

Head Loss

It puts into a relation pressure and velocity in an inviscid incompressible flow.Bernoulli’s equation derivation part 1. Along a low speed airfoil , the flow is incompressible and the . The conservation of kinetic, potential, and flow energies of a fluid stream and their conversion to each other is dictated by the Bernoulli principle.Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. p1 +ρgh1 = p2 + ρgh2. This principle is widely used in the study of the flow of water, air, or .Bernoulli’s equation can be modified based on the form of energy it contains. P 1 + 1 2 ρ v 1 2 = P 2 + 1 2 ρ v 2 2. Fluid Mechanics. Following are the applications of Bernoulli’s equation: Bernoulli’s equation is applied to all problems of incompressible fluid flow. We’ve seen that the nonlinear Bernoulli equation can be transformed into a separable equation by the substitution \(y=uy_1\) if \(y_1\) is suitably chosen.Let us check this out.Bernoulli’s equation in that case is. Bernoulli’s equation focuses on mechanical-energy conservation along a streamline. Most students reading this will have a fairly extensive use of Equation \ref{3.Bernoulli’ s Principle and the Impro vised V enturi Meter.

Bernoulli’s Equation

Bernoulli’s theorem is the principle of energy conservation for ideal fluids in steady, or streamline, flow and is the basis for many engineering applications.Bernoulli’s Equation is not universally applicable. Bernoulli’s theorem implies, therefore, that if the fluid flows horizontally so that no change in gravitational potential energy occurs, then a decrease in fluid pressure is associated . The fluid must be incompressible. Another useful application of the Bernoulli equation is in the derivation of Torricelli’s law for flow out of a sharp edged hole in a reservoir. The Bernoulli’s equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids.Daniel Bernoulli had given this principle.The Bernoulli equation is a fundamental equation in fluid mechanics that relates the pressure, velocity, and elevation of a fluid flowing in a continuous, steady manner. Bernoulli’s equation must be used since the depth is not constant. 2) + ȡg (y2 – y1), states that the. A streamline can be drawn from the top of the reservoir, where the total energy is known, to the exit point where the static pressure and . To develop the governing equation, consider the free body diagram of a beam element in bending shown in Fig. He published this principle in his book called “Hydrodynamical” in the year 1738.

BERNOULLI'EQUATION DERIVATION|WHAT IS BERNOULLI'S EQUATION|EASY ...

Still, it can also be derived in several other ways. We consider water flowing from the surface (point 1) to the tube’s outlet (point 2). Bernoulli’s equation can be applied in Venturi meter, Nozzle meter, Orifice meter, Pitot tube, etc. The middle term is the work done .Bernoulli’s equation describes the relation between velocity, density, and pressure for this flow problem.

What are the 4 assumptions of the Bernoulli’s equation?

Bernoulli’s Equation Explained The core of Bernoulli’s Equation is the conservation of energy — which states that for a closed system, the total energy of the system must remain constant. Power in fluid flow is given by the equation (P1 + 12ρv2 + ρgh)Q = power ( P 1 + 1 2 ρ v 2 + ρ g h) Q = p o w e r, where the first term is power associated with pressure, the second is power associated with velocity, and the third is power associated with height.Other Nonlinear Equations That Can be Transformed Into Separable Equations.Bernoulli’s Equation. The first term on the left is the kinetic energy per unit mass. Bernoulli’s Equation. Bernoulli’ s equation, p1 – p2 = ½ ȡ(v2. but to use it, you have to pick two positions along the pipe and write an equation stating that the value of the unnamed sum of terms is the same at one of the positions as it is at the other. P1 + 1 2ϱ v2 1 + ϱgh1 = P2 + 1 2ϱ v2 2 + ϱgh2.C B is constant along any one streamline, but different streamlines can have different C B values. It has been derived here as a particular degenerate case of the general energy equation for a steady, inviscid, incompressible flow.