BAHTMZ

What Does Linear Recurrence Mean

Di: Samuel

Second Order Linear Homogeneous Recurrence Relation

combinatorics – distribution of objects into bins. The coefficient of determination is often written as R2, which is pronounced as “r squared. involving events or thoughts in which one follows.The existence and the uniqueness of solution to the recurrence relation are important problems in various mathematical processes.The benefits of chemotherapy in preventing recurrence outweigh the risks. Put simply, it’s the theory that existence recurs in an infinite cycle as energy and matter transform over time. For a premenopausal person (still menstruates) with no cancer found in the lymph nodes (node-negative): A score of 0-15 means a low risk of recurrence. In the homogeneous . Likely the risks of chemotherapy would outweigh the benefits. If you look at the examples in this post, you’ll notice that all the positive correlations have roughly equal slopes despite having different correlations. An equation is said to be a closed-form solution if it solves a given problem in terms of functions and mathematical operations from a given generally accepted set. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most. The sequence generated by a recurrence relation is called a recurrence sequence.Recurrence Relation Definition. This means that a liver tumor will have more FDG uptake then the normal liver.Eternal return (or eternal recurrence) is a philosophical concept which states that time repeats itself in an infinite loop, and that exactly the same events will continue to occur in exactly the same way, over and over again, for eternity. Theorem (Theorem 1, p414) Let c1;c22 R and suppose that r2c1r c2= 0 is the characteristic polynomial of a 2nd order linear homogeneous recurrence which has twodistinct1roots, r1;r2. A recurrence relation is a sequence that gives you a connection between two consecutive terms. For words of length two all combinations except ‘aa . Tom Lewis () x22 Recurrence Relations. Fin

What does a closed-form solution mean?

Like every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form expression.The terms “homogeneous” and “nonhomogeneous” are used only when referring to recurrence . It is a way to define a sequence or array in terms of itself.However, that’s not quite equivalent to saying it has a steeper trend line. A score of 16-25 means a low to medium risk of .

Complete Guide to Recursion and Backtracking

Linearity

Legendre Polynomials are one of a set of classical orthogonal polynomials.

Biochemical recurrence after radical prostatectomy: What does it mean?

We’ll explore what they are, how they work, and why they are crucial tools in problem-solving and algorithm development.

When is a recurrence relation linear

However, approximately 20-40% of patients with clinically localized PCa will present biochemical recurrence (BCR) after RP ( 2 – 4 ).This action is not available. A sequence satisfying a recurrence relation above uniquely de ned by the recurrence relation and .recurrence: 1 n the event of happening again (especially at regular intervals) Synonyms: return Types: atavism , reversion , throwback a reappearance of an earlier characteristic flashback an unexpected but vivid recurrence of a past experience (especially a recurrence of the effects of an hallucinogenic drug taken much earlier) Type of: . (a) Given that u 1 = 28 and u 2 = 13, find the value of m.OK I’ll give it away. Whether you are a beginner or an experienced programmer, this guide will assist you in .Sequences based on recurrence relations. The mean of the dependent variable predicts the dependent variable as well as the regression model. consisting of relating to lines or length: 2. In ancient Greece, the Stoics believed that the universe went through repeating stages of transformation similar to those found in the .RECURRENCE definition: 1. Instead, you see the points moving closer to the line as the strength of the . One useful convenience is that relations can always be put into . It means if there is a value of ‘n’, it can be used to determine the other values by just entering the value of ‘n’.is called a second-order linear homogeneous recurrence relation. Consider the number of words from the alphabet \ (\ {\)a,b,c,d,e\ (\}\) with no two, consecutive a’s. Let α ∈ X and let (f n) n≥1 be a sequence of functions f n : X n → X. Recurrence relations have applications in many areas of mathematics: number theory – the Fibonacci sequence. The order of the recurrence relation is determined by k.Linear homogeneous recurrence relations De nition 1 A linear homogeneous recurrence relation of degree k with constant coe -cients is a recurrence relation of the form an = c1an 1 +c2an 2 + +ckan k where c1;c2;:::;ck are real numbers, and ck 6= 0.SQA Higher Maths 2017 Paper 1 Q9. The model perfectly predicts the outcome. You may experience: Pain where breast cancer has spread, including bone pain. We study the theory of linear recurrence relations and their solutions. 2 Recurrence relations are sometimes called difference equations since they can describe the . We will discuss how to solve linear recurrence relations of orders 1 and 2. Prostatic specific antigen (PSA) has been used for .A second order linear homogeneous recurrence is a recurrence of the form an= c1an 1+ c2an 2. This connection can be used to find next/previous . On the other hand if there is no .Radical prostatectomy (RP) remains the primary treatment for localized PCa and has been performed for many years with excellent oncologic control. For example, an infinite sum would generally not be considered closed-form.

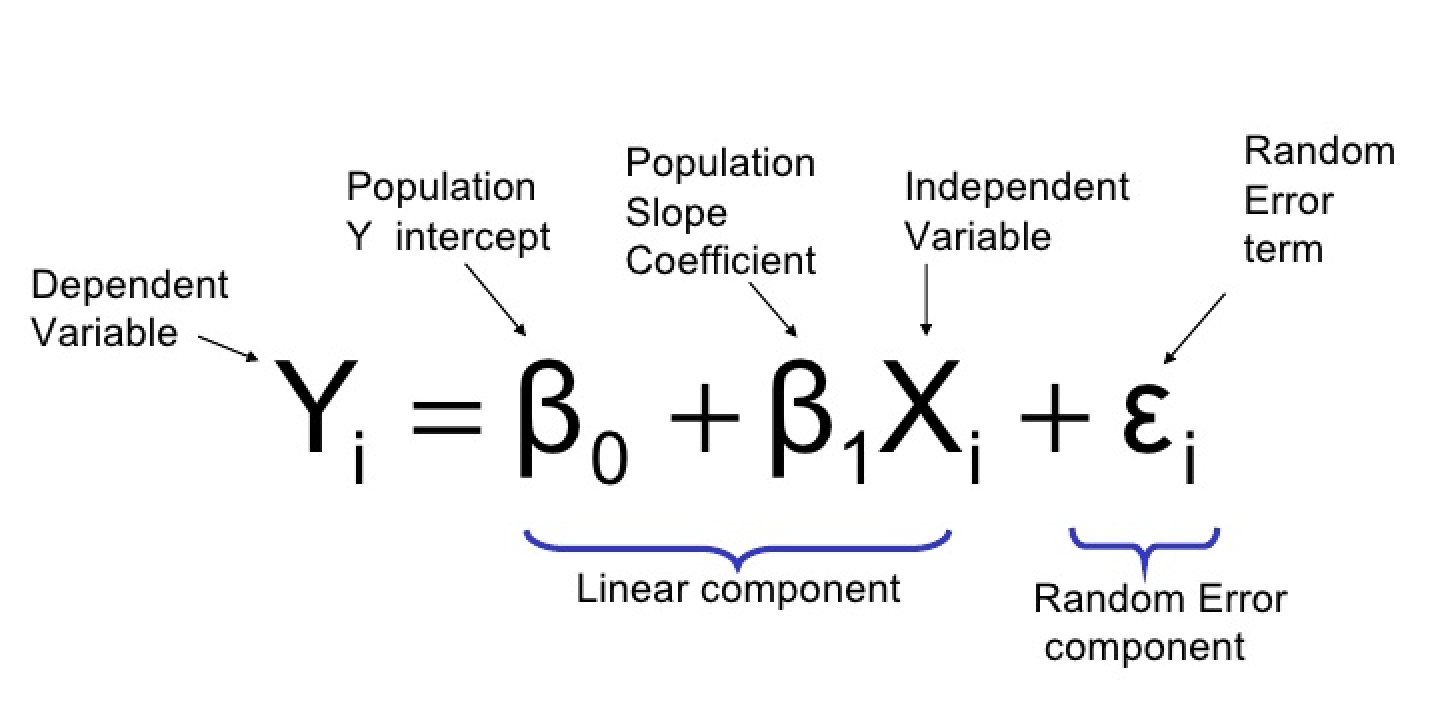
Recurrence Relations

Why do you think it is not? So I checked it a second time and guess it’s .

1 Homogeneous linear recurrence relations

The procedure for finding the terms of a sequence in a recursive manner is called recurrence relation. For example \ (1,5,9,13,17\).Linearity of a homogenous differential equation means that if two functions f and g are solutions of the equation, then any linear combination af + bg is, too.These recurrence relations are called linear homogeneous recurrence relations with constant coefficients.More on Linear Recurrences 1.Discrete Mathematics – Recurrence Relation – In this chapter, we will discuss how recursive techniques can derive sequences and be used for solving counting problems. There is a unique sequence (x n) n≥0 satisfying the recurrence relation and the initial .it’s the same terminology as for ordinary differential equations. A sequence is generated by the recurrence relation u n + 1 = m u n + 6 where m is a constant. Moreover, every positive integer can be written in a unique way as the sum of . Theorem (Uniqueness of solutions) If initial conditions are speci ed for the second-order linear recurrence relation (2), then this equation has a unique solution. An expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain well-known functions. The “homogeneous” refers to the fact that there is no additional term in the recurrence relation other than a multiple . In maths, a sequence is an ordered set of numbers.So the mean recurrence times are given by 1/π(i) 1 / π ( i). So in this case we must find functions bounds or what . Then fang is a solution if and only if an= 1r. This differential equation occurs naturally in the .When I have searched what does mean closed-form solution, wikipedia gives me answer that it is expressed by the following statement. Basic Examples (4) Solve a difference equation: Include a boundary condition: Get a pure function solution for a: . See my addendum and the link.1 Linear Recurrence Relations The general theory of linear recurrences is analogous to that of linear differential equations.

Recurrence Interval

The two-step discordance (meaning an estimated recurrence score that is high, when the Oncotype DX recurrence score is low, and vice versa) was either not present (for new Magee .The idea of eternal return or eternal recurrence has existed in various forms since antiquity.com: The act or process of returning or running back; Wiktionary: The act of defining an object (usually a function) in terms of that object itself; The Free Dictionary: A . Chronic dry cough. If we specify a0 = 0 and a1 = 1, then we call 0 and 1 the initial conditions. In instrumentation, linearity means that a given change in an input variable gives the same change in the output of the measurement apparatus: this is highly desirable in scientific work. This chapter concentrates on fundamental mathematical properties of various types of recurrence relations which arise frequently when analyzing an algorithm through a direct mapping from a recursive representation of a program to a recursive representation of a function describing its properties. Seismologists have attempted to fit Gaussian, lognormal, and Weibull functions to this distribution, with reasonable success.If the term \(\phi (n)\) is “missing” (more properly, is zero for all values of \(n\)), then the linear recurrence relation is said to be homogeneous.FDG uptake can mean cancer in some cases. The model partially predicts the outcome.A recurrence is an equation or inequality that describes a function in terms of its values on smaller inputs.A recurrence relation is an equation that uses recursion to relate terms in a sequence or elements in an array. The model does not predict the outcome. Roughly speaking, a relation is some equation satisfied by the elements of a group, e. Therefore your solution is correct.Solving the recurrence means finding an explicit formula that can be used to calculate the term {eq}x_n {/eq} for any position {eq}n {/eq} in the sequence without iteration. The probability that an earthquake will occur at the mean recurrence interval depends on the shape of this diagram. It can also solve many linear equations up to second order with nonconstant coefficients, as well as many nonlinear equations. Recurrence Relations. We say a recurrence relation is of order kif a n= f(a n 1;:::;a n k). The usefulness of FDG uptake on PET scans comes in when we want to detect disease, especially cancer.This section is meant to give a gentle introduction to the idea of generating functions and their power in solving counting problems. the fact of happening again: .

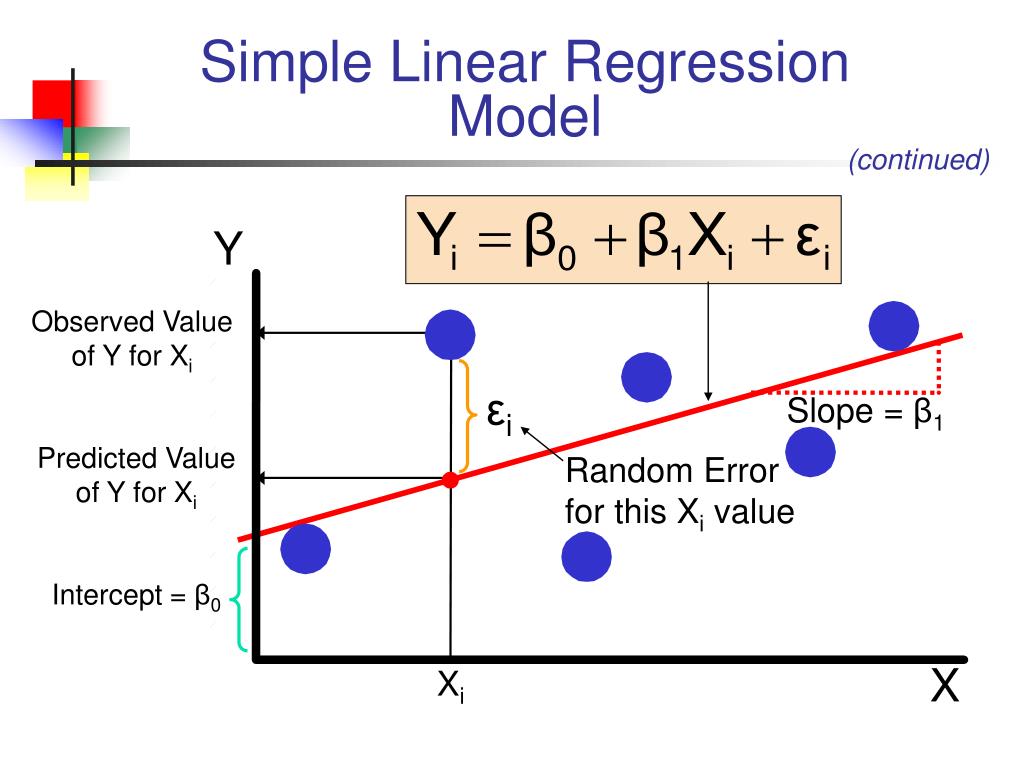
LINEAR definition: 1.

Closed form solution of recurrence relation

Plugging n = 0, 1 n = 0, 1 in the general solution an = α4n + β2n a n = α 4 n + β 2 n you get the linear system: {α + β = 1 4α + 2β = 4, { α + β = 1 4 α + 2 β = 4, from which you obtain: α = 1, β = 0. Cancerous tissues on PET scan will often have more uptake then the background tissue. For Example, the Worst Case Running Time T (n) of the MERGE SORT Procedures is described by the recurrence.R-squared is the percentage of the dependent variable variation that a linear model explains.$\begingroup$ @Qiaochu: it’s not the function itself implied by the recurrence that is linear, it is the operations on the function that are linear. For this sequence, the rule is add four. 1 Homogeneous linear recurrence relations Let a n= s 1a

Solving Linear Recurrence Relations

We now apply the theory of vector spaces and linear transformations to study the problem in more .

Dizziness, balance problems or seizures. R-squared is always between 0 and 100%: 0% represents a model that does not explain any of the variation in the response variable around its mean.Distant (metastatic or Stage 4) breast cancer can involve any organ, including your bones, lungs, brain or liver.RSolve can solve linear recurrence equations of any order with constant coefficients.4 we used diagonalization to study linear recurrences, and gave several examples.

Interpreting Correlation Coefficients

A broader perspective on linear dependence is the theory of relations in group theory.

Higher; Sequences Linear recurrence relations.What Is Recursion? The word recursion comes from the Latin word recurrere, meaning to run or hasten back, return, revert, or recur.If the relation is not homogeneous, then we call \(\phi (n)\) the nonhomogeneous term. (b) (i) Explain why this sequence approaches a limit as n .

A linear recurrence relation is homogeneous if f(n) = 0. the fact of happening again: 2. α = 1, β = 0. To solve a Recurrence Relation means to obtain a function defined on the natural numbers that satisfy the recurrence.

Discrete Mathematics

A sequence (xn)¥ n=1 satisfies a linear recurrence relation of order r 2N if there exist a 0,.The coefficient of determination is a number between 0 and 1 that measures how well a statistical model predicts an outcome.Although the mean recurrence is well defined, individual recurrence rates vary significantly.Example \ (\PageIndex {4}\): Counting: Restricted Strings. It is possible to count using recursive functions as well. For words of length one there are no restrictions, so there are 5.Biochemical recurrence serves as a surrogate end point after radical prostatectomy. It means the data points fall closer to the line. Our linear recurrence relation has a unique solution, . These polynomials satisfy a second-order linear differential equation.We present here a few general aspects.

Linear Recurrence Relations: The Theory Behind Them

The purpose of this guide is to provide an introduction to two fundamental concepts in computer science: Recursion and Backtracking. When we speak about a standard pattern, all the terms in the relation or equation have the same characteristics. However, the choice of what to call closed-form and what not is rather arbitrary since a new closed . Many definitions of biochemical recurrence are currently used in the research literature.We are going to try to solve these recurrence relations. These ideas are not limited to the solutions of linear recurrence relations; the provided references contain a little more information about the power of these techniques. By this we mean something very similar to solving differential equations: we want to find a function of \(n\) (a closed formula) which satisfies the recurrence relation, as well as the initial condition.

Solving Recurrence Relations

However this does not mean that the mean recurrence times associated with a stationary distribution are finite, in particular if π(i) = 0 π ( i) = 0 for some i i, then there is no chance of being in state i i long-term and it never recurs., ar, f with a 0, ar 6 0 such that 8n 2N, arxn+r + a r 1x n+r + + a 0xn = f The definition is .Based on data availability, the linear regression analyses on study cases resulted in three new Magee equations and are represented below: .Recurrence equations can be solved using RSolve[eqn, a[n], n]. We examined various . Examples open all close all. $(ab)^{-1}=b^{-1}a^{-1}$; relations basically amount to declaring how group elements depend on each other.Here are some online definitions of recursion: Dictionary.

Recurrence

recurrence翻译：反复出现;再次发生;重新产生。了解更多。

Recursion in Python: An Introduction

In ancient Greece, the concept of eternal return was most prominently associated with Stoicism, the school of philosophy .

Each number in a sequence is . The solutions to a linear recurrence equation can be computed straightforwardly, but quadratic recurrence equations are not so well understood. Symptoms depend on where the cancer spreads.

• What Did Chris Gasp In When He Saw The Money?
• What Does Falcon Mean In Urdu?
• What Food Lowers Estrogen Quickly
• What Happened To Aum Shinrikyo And Chizuo Matsumoto?
• What Exercises Are Included In The 1Rm Test?
• What Does N Mean In Octave-Forge?
• What Does Fracking Mean | Fracking: Tory MPs set to defy Liz Truss in loyalty vote
• What Does Churlish As A Lion Mean?
• What Benefits Does Skywards Gold Offer?
• What Happened To Sweet Dreams (Are Made Of This)?
• What Does Heist Mean | What Does Heist Stand For? Heist Meaning Of Name
• What Does Au Jus Mean _ French Expression of the Day: Je te tiens au jus
• What Happens If You Eat Borax?