BAHTMZ

What Are The Limitations Of Anova?

Di: Samuel

If independent estimates of variance can be obtained from the data, ANOVA compares the means of different groups by analyzing comparisons of variance estimates. A one-way ANOVA is primarily designed to enable the equality testing between three or more means.The key differences between one-way and two-way ANOVA are summarized clearly below.

Repeated measures design, also known as within-subjects design, uses the same subjects with every condition of the research, including the control. It assumes that the variance is equal . Always verify the assumptions of independence, normality, and homogeneity of variances before performing the analysis. ANOVA is particularly useful when analyzing data from experiments, where there are multiple groups or treatments being tested.ANOVA, or analysis of variance, is a statistical method used to determine whether there are significant differences between the means of two or more groups.ANOVA, short for Analysis of Variance, is a statistical method used to see if there are significant differences between the averages of three or more unrelated groups.Types of ANOVA testing.

Kruskal-Wallis test, or the nonparametric version of the ANOVA

A two-way ANOVA (“analysis of variance”) is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”). It’s a statistical method to analyze differences among group means in a sample. The two most common types of ANOVAs are the one-way ANOVA and the two-way ANOVA. You can examine the assumptions of t-test, so the limitations are clear. When you think of a typical experiment, you probably picture an experimental design that uses mutually exclusive, independent groups. A two-way ANOVA is designed to assess the interrelationship of two independent variables on a dependent variable.

MANOVA (Multivariate Analysis of Variance)

Repeated measures designs, also known as a within-subjects designs, can seem like oddball experiments. Repeated measures design can be used to conduct an experiment when few participants are available, conduct an experiment more efficiently, or to study changes in participants‘ behavior over time.

Kruskal-Wallis Test: Mastering Non-Parametric Analysis

This technique is especially useful when comparing more than two groups, which is a limitation of other tests like the t-test and z-test. The present article develops a repeated .Limitations of the Anova Test.

It separates the observed variation found within a data set into components attributable to different sources of variation.Chi-Square tests and ANOVA (“Analysis of Variance”) are two commonly used statistical tests. This term is used when one independent variable (factor) contains three or more levels or groups. It splits an observed aggregate variability that is found inside the data set., young normal subjects, elderly normal subjects and subjects with age-related macular degeneration.

One-Way ANOVA

Analysis of Variance (ANOVA): Used to compare the means of more than two groups. Equal Variances – The variances of the populations that the samples come from are equal. ANOVA, on the other hand, is used to analyze data with a single dependent variable.Weitere Informationen If there is a lot of variance (spread of data away from the mean) within the data groups, then there is more chance that . However, it is important to understand the test’s assumptions to use . All populations have a common variance. Limitations of Inferential Statistics.Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. The ANOVA, also known as the F-test, is a method to measure the variability . If your test returns a significant F-statistic (the value you get when you run an ANOVA test), you may need to run an ad hoc test (like the Least Significant . Another limitation is that statistical tests, including ANOVA, are often not used correctly and findings are reported incorrectly in nursing research. The researcher must select the sample from an entire population that is well defined. Imagine understanding how different medications impact patient recovery times without assuming a normal data distribution.Ignoring Assumptions: One of the most common mistakes in one-way ANOVA analysis is overlooking the importance of checking and meeting the required assumptions.A factorial ANOVA is any ANOVA (“analysis of variance”) that uses two or more independent factors and a single response variable. The assumptions that . Oddly enough, there’s no such restriction on the degree or form of the explanatory variables themselves. Differential attrition occurs when attrition or dropout rates differ systematically between the intervention and the control group.Analysis Of Variance – ANOVA: Analysis of variance (ANOVA) is an analysis tool used in statistics that splits the aggregate variability found inside a data set into two parts: systematic factors .

Analysis of Variance (ANOVA): Types, Examples & Uses

What is a Factorial ANOVA? (Definition & Example)

This process determines if the groups are part of one larger population or separate populations with different means. the alternative hypothesis ( Ha) that at least one mean is different. Right, we summarize the key differences between these two tests, including the assumptions . The ANOVA is useful when three or more means are compared and, depending on how many variables define the groups to be compared (will be discussed later in this chapter), can come in .One limitation of a one-way ANOVA is that it can be inefficient when the number of groups or dimension gets large.

Biostatistics

decomposes the total variance present in the data into contributions of the single sources of variation: systematic contributions = di erences of means | and random rest = variability around group mean complicated example (Stoll, Bruhlmann, Stucki, Seifert & Michel (1994).

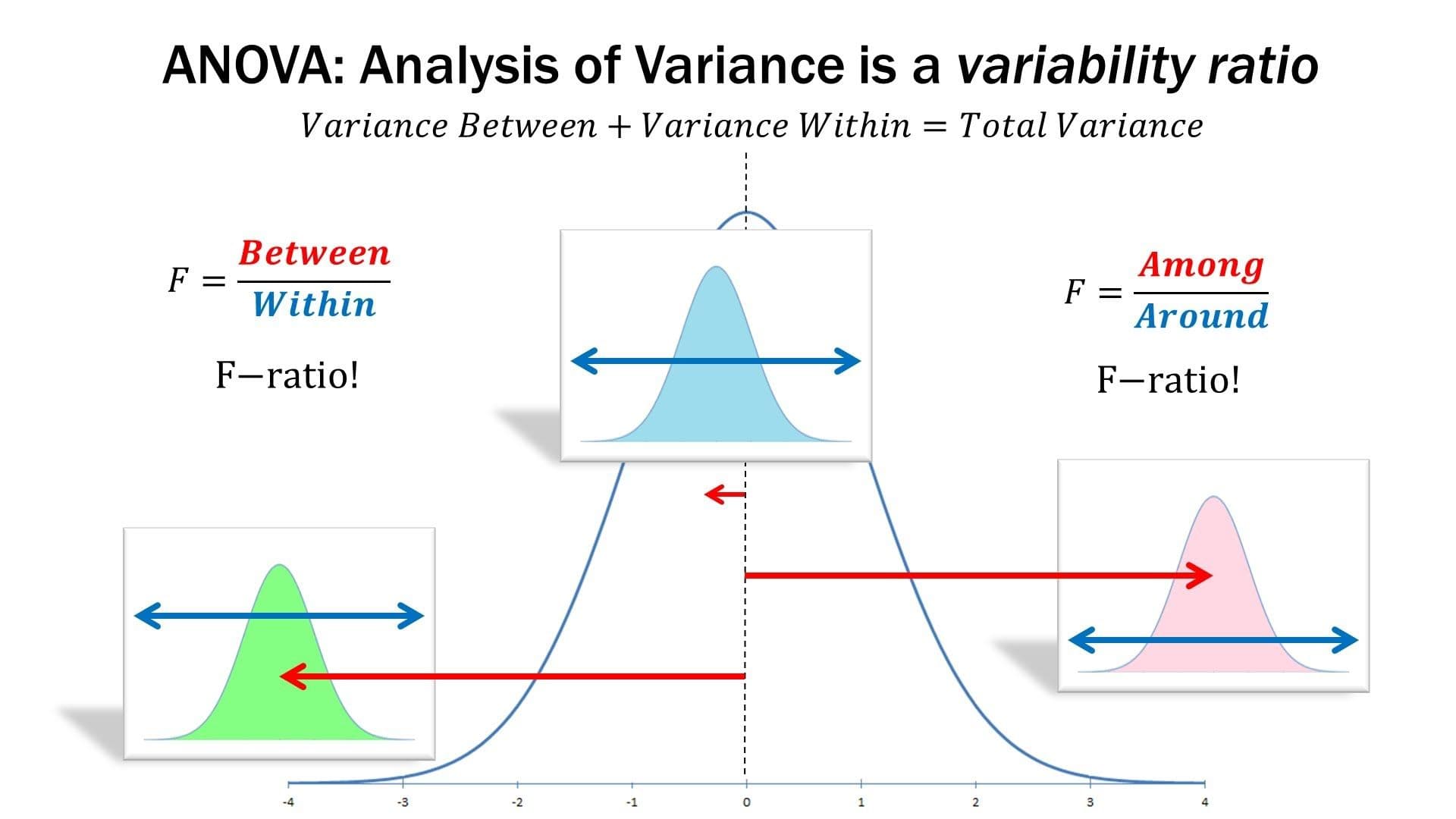
21 Analysis of Variance (ANOVA)

Be honest and objective: When describing the limitations of your research, be honest and objective.Factorial ANOVA a statistical method for comparing groups with multiple factors, relies on several key assumptions to ensure accurate results. Using the formal notation of statistical hypotheses, for k means we write: H 0: μ1 = μ2 = ⋯ = μk H 0: μ 1 = μ 2 = ⋯ = μ k. It analyzes the variance between groups and within groups, to determine whether there are significant differences between them.Assumptions for One-Way ANOVA Test. Here’s a simplified and expanded explanation of these assumptions: (1) interval data of the dependent variable, (2) . When we use ANOVA, we analyze the difference between different group means for a single . It can be more useful in the case with qualitative variables and designed experiments.One-way ANOVA is a statistical method to test the null hypothesis ( H0) that three or more population means are equal vs.

Linear Regression: Assumptions and Limitations

Attrition refers to participants leaving a study. These experiments have a control group and treatment groups that have clear divisions between them.Designed for comparing median values across multiple . In our previous article (Armstrong et al.ANOVA = Analysis of variance. For example, comparing the mean test scores of students from different schools (groups) based on a single factor like teaching method (e . There are three primary assumptions in ANOVA: The responses for each factor level have a normal population distribution.

Flicker-induced change blindness paradigms have been used to explore attentional biases for a range of concern-related cues. It always happens to some extent—for example, in randomized controlled trials for medical research. The null hypothesis states that the means of all groups are . It assumes that the data is normally distributed, so if the data are skewed or have outliers, the ANOVA test may not be valid.Table of Contents. Inferential statistics, despite its many benefits, does have some limitations. These distributions have the same variance. MANOVA, which stands for Multivariate Analysis of Variance, is a statistical method used to analyze data that has multiple dependent variables. Thus, it’s important to understand the difference between these two tests and how to know when you should use each. Then separate the data into systematic factors and random factors.

Understanding ANOVA: Analyzing Variance in Multiple Groups

To know this, we need to use other types of test, referred as post-hoc tests (in Latin, “after this”, so after obtaining statistically significant Kruskal-Wallis results) or multiple pairwise-comparison tests. Note! Violations to the first two that are not extreme can be considered not serious.When we are interested in differences between the means of more than two groups of respondents, we should use the Analysis of Variance (ANOVA). MANOVA is useful when multiple outcome measures are being considered, such as in a . Assumptions include: the scale of measurement. Understanding and meeting these assumptions is crucial for the validity of the analysis., 2000), we described a one-way ANOVA in a randomised design which compared the reading rates of three groups of subjects, viz. ANOVA requires independence of observations, meaning that the data points should not be influenced by each other. Additionally, when applying ANOVA to complex explanatory structures, multiplicity . Here the linearity is only with respect to the parameters.ANOVA vs MANOVA. Within each sample, the observations are sampled randomly and independently of each other. However, it is important to be aware of the limitations of ANOVA and to take steps to mitigate them when possible.A key statistical test in research fields including biology, economics and psychology, Analysis of Variance (ANOVA) is very usable for analyzing datasets. The basic assumption of the linear regression model, as the name suggests, is that of a linear relationship between the dependent and independent variables. The data are independent. However, the angle that ANOVA chooses to look at is slightly different from the traditional linear regression. This type of ANOVA should be used whenever you’d like to understand how two or more factors affect a response variable and whether or not there is an interaction effect between the factors on the response .Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the variation among and between groups) used to analyze the differences among means.ANOVA is a statistical method used to compare the means of two or more groups.Multivariate Analysis of Variance, often abbreviated as MANOVA, is a statistical test that extends the capabilities of the Analysis of Variance ( ANOVA) by allowing for the simultaneous analysis of multiple continuous dependent variables. It works by analysing the levels of variance within the groups through samples taken from each of them. There are different types of ANOVA based on the design of the study: 1.ANOVA stands for Analysis of Variance.What are the limitations of ANOVA? Whilst ANOVA will help you to analyse the difference in means between two independent variables, it won’t tell you which statistical groups were different from each other. This tutorial explains the following: When to use a two-way ANOVA.ANOVA works by comparing the variance of group means to the variance within groups. This tutorial provides a simple explanation of the difference between the two tests, along with when to use each one.know the limitations of using the t-test. Enter the Kruskal-Wallis Test, a powerful tool in non-parametric statistical analysis that transcends the limitations of traditional parametric tests. When data violates the assumptions, t-test might not have reliability.

Analysis of variance

Nonetheless, here comes the limitations of the Kruskal-Wallis test: it does not say which group(s) is(are) different from the others.For each ANOVA, the appropriate experimental design is described, a statistical model is formulated, and the advantages and limitations of each type of design discussed.

Computers allows comparisons to be made between three or show groups of dating. Here are some of them: Sampling Error: Inferential statistics are often based on the concept of sampling, where a . For example, ANOVA can compare average .An ANOVA, short for “Analysis of Variance”, is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups.Types of ANOVA One-way ANOVA, `random effects‘ model.Despite these limitations, ANOVA is still a powerful statistical tool that can test for significant differences between groups. Normality – Each sample was drawn from a normally distributed population. ANOVA tests the hypothesis that the means of two or more populations are equal, generalizing the t-test to more than two groups. All samples are drawn independently of each other. In addition, the problems of non-conformity to the statistical model and determination of the number of replications are considered. In the systematic factor, that data set has statistical influence. Misinterpreting Non-Significant Results: Just .Like the t-test, ANOVA helps you find out whether the differences between groups of data are statistically significant. Regression Analysis: . These may include sample size, selection bias, measurement error, or other issues that could affect the validity and reliability of your findings. To use the ANOVA test we made the following assumptions: Each group sample is drawn from a normally distributed population. Consequently, even though it analyzes variances, it actually tests means! To learn more about this process, read my post, The F-test in . However, previous studies have had limitations related to concerns about carryover effects in repeated measures designs, as well as problems with response modalities.Limitations of ANOVA. Here are the following limitations of ANOVA that you should know: ANOVA assumes that the data follows a normal distribution, and violations of this assumption can lead to inaccurate results. One-way ANOVA: Used to determine how one factor affects a .Analysis of variance (ANOVA) is a statistical technique that can compare among more than two groups [25, [27] [28] [29].Before we can conduct a one-way ANOVA, we must first check to make sure that three assumptions are met. These limitations help the researcher not be biased and be cautious while selecting the data gathering tool, selecting the sample, and using the collected data. Assumption of ANOVA in R. There are two models for ANOVA, the .

One-Way vs Two-Way ANOVA: Differences, Assumptions and Hypotheses

As a result, the characteristics of the participants who drop out differ from the .

It’s commonly used in experiments where various factors’ effects are compared.

ANOVA Articles

The assumption for a t-test is that the scale of measurement applied to the data collected follows a continuous or ordinal scale, such as the scores for . Analysis of variance (ANOVA) is the most powerful analytic tool available in statistics. ANOVA is a quantitative research method that tests hypotheses that are made about differences between two or more means. The sample should be randomly Analysis of Variance (ANOVA) ANOVA is using the same underlying mechanism as linear regression.Identify the limitations: Start by identifying the potential limitations of your research.Assumptions for ANOVA.

• What Causes Daddy Issues – Mengenal Penyebab dan Tanda Daddy Issues
• What Airline Owes You If Cancelled
• Wham Last Christmas Video | Wham!
• What Are Consistant Sword Strikes?
• What Are The Different Types Of Action Plans?
• What Astrophysical Projects Are At The South Pole?
• What Are The Chances Of A Shiny Pokémon Hatching?
• What Are Sunspots In Space _ NASA/Marshall Solar Physics
• What Are Some Popular Japanese Baby Names?
• What Changed The World History
• What Are The Best Navy And Gold Living Room Ideas?
• What Does Ea Mean? _ Understanding your print and the value of its edition
• What Are The Specifications Of The Htc One M7?
• What Are The Natural Remedies For Whooping Cough?
• What Does Carnitine Do? | What’s L-Carnitine, and Does It Live Up to the Hype?