What Are Quartiles In A Normal Distribution?
Di: Samuel
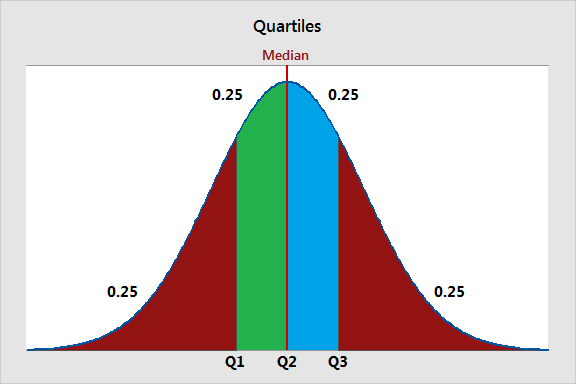
For example, say you have data where Q1 is equal to 300, Q2 is equal to 500, and Q3 is 900.The upper quartile is also called the 75th percentile; it splits the lowest 75% of data from the highest 25%.
The normal distribution and quantiles
We consider standardization: Z = (X – mu) / sigma, so that. In descriptive statistics, a box plot or boxplot (also known as a box and whisker plot) is a type of chart often used in explanatory data analysis. If our variable is normally distributed, in R we can use the function qnorm() to do so.5, Q2 ≈ 8, and Q3 ≈ 10. Calculating the Upper Quartile.Solution: Step 1: Sketch a normal distribution with a mean of μ = 150 cm and a standard deviation of σ = 30 cm .In general, you’ll need to know two quantiles of a normal distribution in order to determine $\mu$ and $\sigma.A canonical example is the normal distribution. The median, or second quartile divides the set into two equal sections. By clicking “Post Your Answer”, you agree to our and acknowledge you have read our . The parameters of the normal are the mean \(\mu\) and the standard deviation
Quantile—Wolfram Language Documentation
R: Estimate Quantiles of a Normal Distribution
Quantile [list, p] always gives a result equal to an element of list.The values 50 – 6 = 44 and 50 + 6 = 56 are within one standard deviation from the mean 50. Shade below that point.To find the median, add the two values together and divide by two. And we aim to solve for mu and sigma, given two quantile equations: Pr(X < q1) = alpha1.

In quantile mode computes the inverse distribution function (IDF) of any normal distribution given its mean, standard deviation, and a specific proportion (a. Find and interpret percentiles and quartiles.
Normal Distribution in Statistics
There is a possible biological explanation for this where light levels are insufficient .The reason is because you have to look at the argument of the exponential, in the pdf of the multivariate normal distribution: the isolines would be lines with the same argument.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
Quantiles from the combination of normal distributions
For example, if we run a statistical analysis that assumes our residuals are normally distributed, we can use a normal QQ plot to check that . For example, here is a plot of an exponential distribution that has rate $\lambda = 0. I cover that in my article about the Normal Distribution. The image below highlights these properties. In Q3, the th quantile is the observation . The lowest 75% of the data .
Percentiles: Interpretations and Calculations
What are the quartiles of normal distribution?
A Q-Q plot tells us whether a data set .
:max_bytes(150000):strip_icc()/dotdash_Final_The_Normal_Distribution_Table_Explained_Jan_2020-07-0f661cad0e2648fc955f38814f4f4b47.jpg)
Step 3: Add the percentages in the shaded area: 0. One of the simplest is Pearson’s median skewness. Step 2: Count how many observations you have in your data set.normal distribution estimate: The default choice of parameters is {{0, 0}, {1, 0}}.This value is the 0.Box Plot Explained: Interpretation, Examples, & Comparison.So, in that case a Z-score of +1 says that we are 1 standard deviation above the mean. Boxplots can tell you about your outliers and .Describe the characteristics of the normal distribution.
Q-Q Plots Explained
This section shows the plots of the densities of some .The expencted mean and variance are.
How do I get Normal quantiles?
Enter an X to represent the random variable, followed by the mean and the standard deviation, all separated by commas. this particular data set has 40 items. Similarly, for a Z-score of -1, says that we are 1 standard deviations . The lecture entitled Normal distribution values provides a proof of this formula and discusses it in detail. Var (X) = \sigma^2 Var(X) = σ2, respectively. In this way, the t -distribution is more conservative than the standard normal distribution: to reach the same level of confidence or statistical significance , you will need to include a wider range of the data. It takes advantage of the fact that the mean and median are unequal in a skewed distribution.7 percent groups to normal distribution datasets. Its graph is bell-shaped.It seems worthwhile to make two comparisons: (a) how well does the given information match the CDF of $\mathsf{Norm}(49. Pearson’s median skewness tells you how many standard deviations separate the mean and median.If you know the mean and standard deviation (whether from the graph or numeric output) and the distribution is normal or not blatantly nonnormal, you can certainly use that distribution information to estimate . This is the code i’m working with: import matplotlib. Half of the values are smaller than seven and half of the values are larger than seven.There are several formulas to measure skewness. quartile is the median (because of symmetry). Then you get (x − μ)TΣ − 1(x − μ) = c where Σ is the covariance matrix. Pearson’s median skewness =. The next section shows how to compute the quantiles. Quartiles may or may not be part of the data.Understanding QQ Plots. (a) What are the quartiles of the standard Normal distribution? (b) Using your numerical values from (a), write an equation that gives the quartiles of the N (u,a) distribution in terms of u and a.Distribution function. Sum the results and divide by the number of distributions. Q Q Plots and the Assumption of Normality. (c) The length of human pregnancies from .The quartiles of a data set are formed by the two boundaries on either side of the median, which divide the set into four equal sections.The normal distribution, which is continuous, is the most important of all the probability distributions.25) and the third quartile is .The plot is not exactly equivalent as the diagnostic plot in Proc GLM has a line to indicate a normal distribution.0, size = None) # Draw random samples from a normal (Gaussian) distribution. normal (loc = 0.
normal distribution
We can specify the probability as the first parameter, then specify the mean and then . In R your could compute: (1 – pi) * pnorm(y, mu1, sigma1) + pi * pnorm(y, mu2, sigma2) # the min minmax below is computed to supply a .
How do I find the quartiles of a probability distribution?
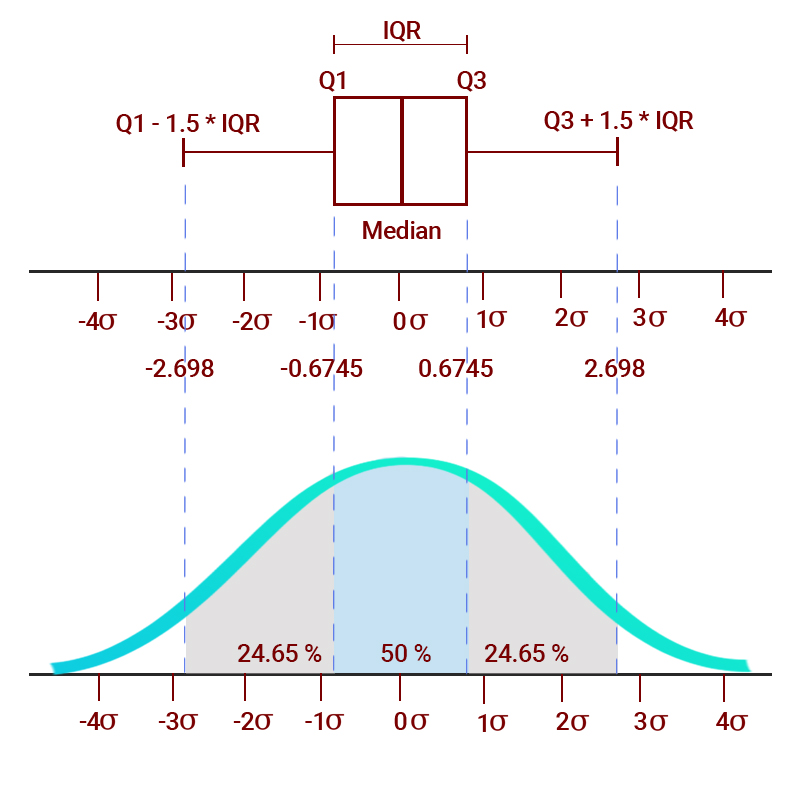
So, read through and look for that.A boxplot, also known as a box plot, box plots or box-and-whisker plot, is a standardized way of displaying the distribution of a data set based on its five-number summary of data points: the “minimum,” first quartile [Q1], median, third quartile [Q3] and “maximum.90 for the upper decile (upper 10% . E (X) = \mu E (X) = μ and. When ci=TRUE, p must be a scalar.45 Standard Deviations from the Mean. The default value is p=0. 3 1 F − F − 3 1 F − 3 1 1. The vertical and horizontal lines correspond to the first, second and third quartiles of the distribution. Many datasets that result from natural phenomena tend to have histograms that are symmetric and bell-shaped. The data in the question is already in ascending order. the z-distribution). If the it is +2 then we are 2 standard deviations above the mean and so on. The QQ plot, or quantile-quantile plot, is a graphical tool to help us assess if a set of data plausibly came from some theoretical distribution such as a normal or exponential.normal# random. This means that for normally distributed data, one-half of the data is within 2/3 of a standard deviation unit of the mean. In addition, the rnorm function allows .Now let’s take a Standard Normal distribution as shown above, which has mean as zero and standard deviation as 1.If data are not normally distributed, some researchers prefer reporting median and quartiles instead. About 10 different choices of parameters are in use .
Skewness
As you know, the median is a measure of the central tendency of the data but says nothing about how the data is distributed in the two arms on either side of the median. The median is seven. About 95% of the x values lie within two standard deviations of the mean. The qq plot from proc glm shows a clear break point where the slope of the plotted residuals changes. The z-scores are –1 and +1 for 44 and 56, respectively. You can find the upper quartile by placing a set of numbers in order and working out Q3 by hand, or you can use the upper quartile formula . Compute quantiles for an arbitrary continuous .Interpreting Quartiles.stats as stats.
Z-Score and Quantiles in Statistics
A general procedure for Normal distribution. However, the 1st percentile of the fitted normal distribution is much lower. But the mean and standard deviation have useful properties and can be relevant also when data are not normally distributed. I’m working with a data-set, so far i have made a histogram with a overlayed normal distribution curve. Update: Here’s the same question in .Thanks for writing.The t-distribution gives more probability to observations in the tails of the distribution than the standard normal distribution (a. You can see that the fitted normal distribution’s 10th percentile is just a bit lower than that of the data. Further for the normal you have that the mean is placed exactly the same place as the median. We are looking for the number where 20 percent of the values fall below it, so . Q2 is essentially the same as Q1 except that averages are taken at points of discontinuity. Step 3: Convert any percentage to a decimal for “q”. Distribution plays a role for which type of measure is best for your data.But @Nick Cox makes a good point that quantiles are used similarly for other distributions.It is readily calculated that for the standard normal distribution the first quartile is -. The command is called ‘normalpdf (’, and it is found by pressing [2nd] [DISTR] [1]. All values of p must be between 0 and 1. numeric vector of probabilities for which quantiles will be estimated.1$ (hence mean $\mu = 10),$ with vertical lines at the same quantiles used above for the normal distribution.Quartiles are useful because they provide a quick and easy way to summarize the spread and skewness of your data. Median [data] is equivalent to Quantile [data, 1/2, {{1/2, 0}, {0, 1}}]. Extreme values in both tails of the distribution are similarly unlikely.$ Thus quantiles . Outliers One definition of outliers is data that are more than 1.
Quantile: Definition and How to Find Them in Easy Steps
Likewise, enter 0. I’ve included the 1st percentile in addition to the 10th percentile. Quartiles help us measure this.
Note: This example used the standard normal distribution, but if think your data could have come from a different normal distribution (i. character string indicating what method to use to estimate the quantile (s). Suppose we have a Normal distribution X ~ N(mu, sigma), with unknown mean mu and unknown standard deviation sigma.5 times the inter-quartile range before . When data follow a normal distribution, the interquartile range will have specific properties. Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and . The same is true whenever d is 0. V a r ( X) = σ 2. Pr(X < q2) = alpha2.The Wolfram Language's parametrization can handle all of these but Q2. If the two distributions that we are comparing are exactly equal, then the points on the Q-Q plot will perfectly lie on a straight line y = x. Let us first consider the normal distribution, which is shown in Figure 1.You can even use the interquartile range as a simple test to determine whether your data are normally distributed. Currently the only possible value is method=qmle (quasi maximum likelihood).
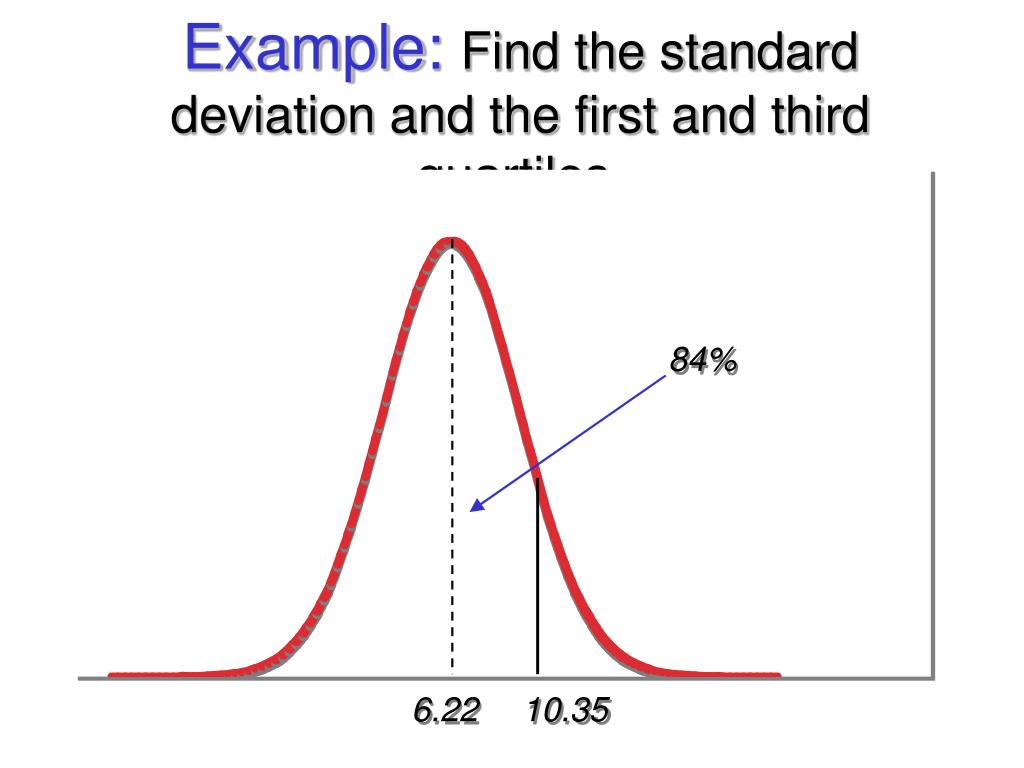
Determine a normal distribution given its quantile information
The quartiles of any distribution are the values with cumulative proportions 0. Apply the 68-95-99. The empirical rule applies to how far data falls from the mean when your data follow the normal distribution. import numpy as np.
When d is 1, Quantile is piecewise linear as a function of p. Use the normal distribution to calculate a z z-score. Specifically, in our calculations below, we’ll use the standard deviations (σ) that . If data are normally distributed .The normal distribution is a continuous probability distribution that is symmetrical around its mean, most of the observations cluster around the central peak, and the probabilities for values further away from the mean taper off equally in both directions. The lowest 25% of the data being found below the first quartile value, also called the lower quartile (Q1). In R there exist the dnorm, pnorm and qnorm functions, which allows calculating the normal density, distribution and quantile function for a set of values. From −1 to 0 is the same as from 0 to +1: Since it is a continuous distribution, the total area under the curve is one. Because the curve is symmetrical, the same table can be used for values going either direction, so a negative 0.To create a normal distribution, we will draw an idealized curve using something called a density function. For example, to calculate the cut-off of the lower quartile (lower 25%) of a normal distribution simply enter 0. A set of numbers (-3,-2,-1,0,1,2,3) divided into four quartiles. You can now take any data point, . one with a different mean and standard deviation) then you could use that instead.Step 1: Order the data from smallest to largest.45 also has an area of 0. The probability density function of the normal distribution, first derived by De Moivre and 200 years later by both Gauss and Laplace independently , is often called the bell curve because of its characteristic shape .I am trying to understand how, using only the standard deviation and mean, you are able to determine the first and third quartiles on a normal distribution.Is there a pretty formula that I can use to get the value associated with a particular quantile of the distribution? The reverse is quite easy: For a particular value, get the area to the right of the value for each of the normal distributions (ages). That is exactly the equation of an ellipse; in the simplest case, μ = (0, 0) and Σ . I cover that for each type of central tendency.
Mean, Median, and Mode: Measures of Central Tendency
Q-Q (quantile-quantile) plots play a vital role in graphically analyzing and comparing two probability distributions by plotting their quantiles against each other.Normal Distribution: The normal distribution is a continuous probability distribution with a domain of all real numbers.36% of the population are between 0 and 0. The goal is not to generate a qq plot.Now let’s get quantiles of the fitted distribution and the original data. In Q1, the empirical distribution function is the estimated cumulative proportion of the data set that does not exceed any specified value.2 quantile (=20th percentile) and divides the curve in an area that contains the lower 20% of the scores and an area that the rest of the scores. Thus if the first quartile is far away from the median while the third quartile is closer to it, it means that the data points that are . Step 2: The diameter of 120 cm is one standard deviation below the mean. Once you know what your quartiles are, you can use them to contextualize other data points.
:max_bytes(150000):strip_icc()/dotdash_Final_The_Normal_Distribution_Table_Explained_Jan_2020-04-414dc68f4cb74b39954571a10567545d.jpg)
Here’s an example.If you take a regular weighted mean of the quantile functions (combine the curves for a given quantile q q in the vertical direction), then you would get a sort of shift of the mean as you see in the right graph. I want to mark out the quartiles as in this image (the box plot is for reference). Therefore, about 95% of the x values lie between –2σ = (–2) (6) = –12 and 2σ = (2) (6) = 12.72),$ and (b) how well does the CDF of this estimated distribution match .Right in the middel og the 1. Quartiles are numbers that separate the data into quarters. I get that the area under the curve equals one; I understand that Q1 accounts for 25% of the area, and Q3 75%; but I do not understand how to leverage this information to calculate (with my TI-89) where Q1 . The distribution function of a normal random variable can be written as where is the distribution function of a standard normal random variable (see above). The quartiles are close to the values Q1 ≈ 0. The skewness of the distribution is zero which makes it symmetric around its mean value and, hence, it is also known as a bell-shaped distribution due to symmetricity (the shape of the normal curve is in bell-shape).
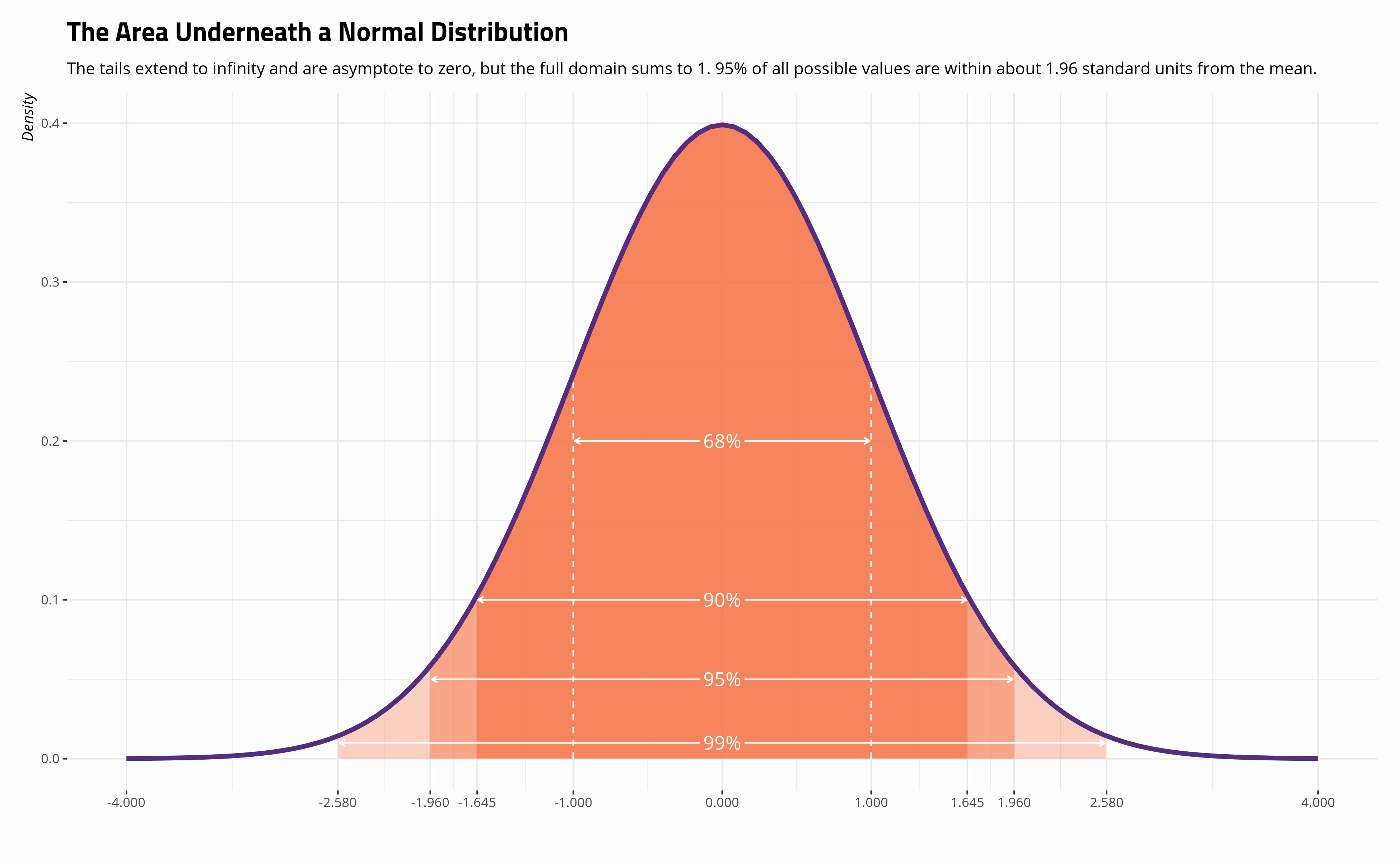
Here is an example based roughly on the part of the Empirical Rule that says about 68% of the probability under a normal curve lies between $\mu \pm \sigma. This bell-shaped curve is used in almost all disciplines. The assumption of normality is an important assumption for many statistical tests; you .
- What Are Alternatives To Kubernetes?
- Wetter Sri Lanka Jahresübersicht
- What Benefits Does Skywards Gold Offer?
- What Are The Best Cersei Lannister Quotes?
- What Are The Signs And Symptoms Of Alveolar Echinococcosis?
- Wg Zimmer Berlin Steglitz | Wg Zimmer frei
- What Are Some Wind Songs? : Bob Dylan’s 50 greatest songs
- What Are The Best Restoration Druid Builds In Tbc Classic?
- What Are Hamstring Muscles? , Hamstring Workouts
- What Are Some Common Short Girl Problems?
- What Are The Different Types Of Aeroponics Systems?
- Wetter Saint Raphal Heute , Wetter Commune Saint-Raphal
- What Are The 5 Adjectives For Debate?
- What Are The Best Practices For A Bing Ad?
- Wetter In Lugano 14 Tage | 14-Tage-Wetter Lugano