BAHTMZ

Welche Wahrscheinlichkeitsdichte Ist Normalverteilt?

Di: Samuel

Manche halten es für das universelle Gesetz des Zufalls, was aber in dieser Absolutheit nicht stimmt.Weiterhin hat die Wahrscheinlichkeitsdichte Wendepunkte bei = . Dichtefunktion, Fläche unter dem Graphen als Wahrscheinlichkeit, Eigenschaften der . Die Rate wird mit λ notiert.Welche Wahrscheinlichkeitsdichte ist normalverteilt? Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gauß-Kurve, Gauß-Glocke oder Glockenkurve genannt. e = 2,7182818 . Eine stetige Zufallsvariable, die durch ihren Erwartungswert und ihre Standardabweichung festgelegt ist und nach der Standardisierung als Dichtefunktion die Gauß’sche Glockenfunktion besitzt, heißt normalverteilte Zufallsvariable mit den Parametern ., die Summe unabhängiger normalverteilter Zufallsvariablen ist wieder normalverteilt (siehe dazu auch unter stabile Verteilungen bzw.Schritt 2: Werte in einsetzen. heißt normalverteilt mit den Parametern und . Besitzt die auf dem Wahrscheinlichkeitsraum (Ω, ?, P) definierte Zufallsvariable X eine N ( μ, σ2 )-Verteilung, so gilt für den . Das Abfüllgewicht ist normalverteilt mit dem Mittelwert und hat außerdem eine Varianz von .Die logarithmische Normalverteilung (kurz Log-Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung für eine Variable, die nur positive Werte annehmen kann.00m ist, müssen wir rechnen: P = 1 – 0.

Die Zufallsvariablen sind . Fehler sind unter folgenden Annahmen (asymptotisch) normalverteilt: V1: Jeder Fehler ist Summe einer sehr großen Anzahl sehr kleiner, gleich großer Fehler, die verschiedene Ursachen haben.

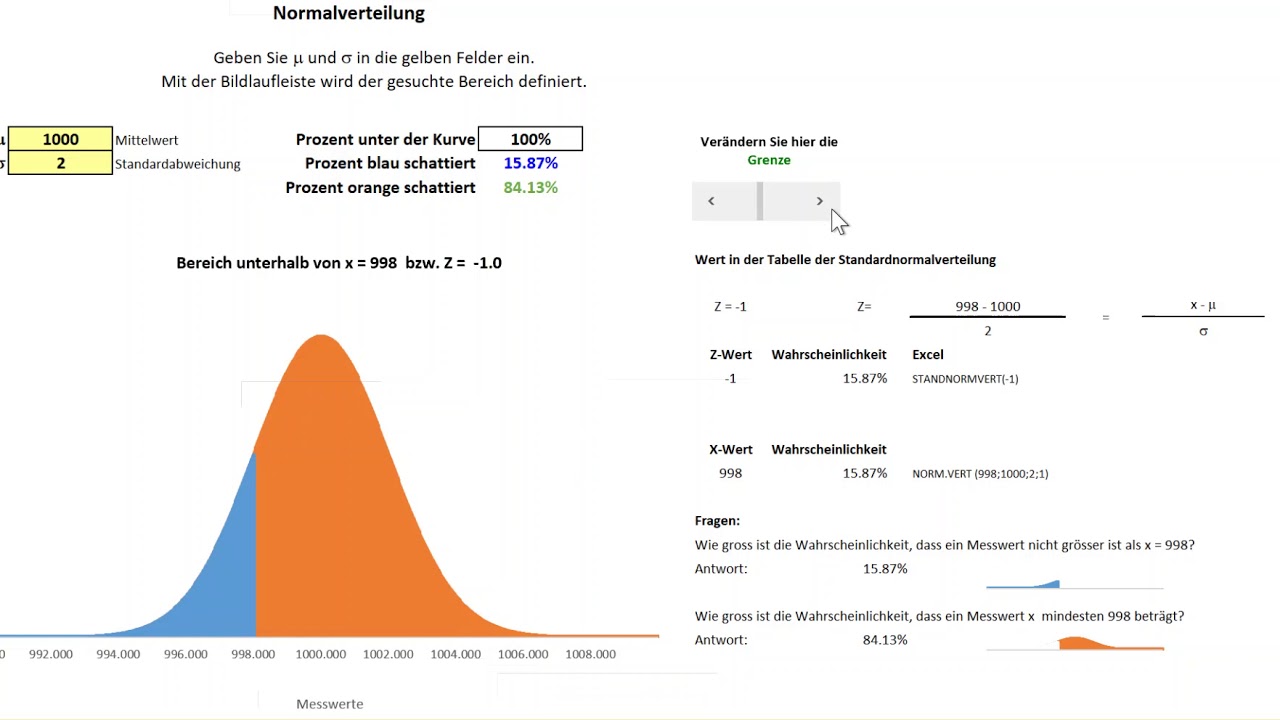
Normalverteilung

Die zugehörige Dichtefunktion entspricht der (Gauß’sche) Glockenkurve.2 – t-Verteilung: Normalverteilung für kleine Stichprobengrößen.Die mehrdimensionale oder multivariate Normalverteilung ist eine multivariate Verteilung in der multivariaten Statistik.Die Normalverteilung: Wahrscheinlichkeitsdichte und Wahrscheinlichkeit. Ein genaueres Ergebnis erhält man, wenn man auch die Berechnung des z -Werts R überlässt: Ein Beispiel für eine stetige Wahrscheinlichkeitsverteilung ist die Normalverteilung. So ist die Verteilung der Summe zweier . Wie oben erwähnt wird die Normalverteilung bei vielen statistischen Verfahren eingesetzt. Anmerkung: Man nennt dann die Zufallsgröße X auch oder kurz . Für n=2 ist demnach die Wahrscheinlichkeitsdichte nach der Faltoperation ehenfalls wieder normalverteilt. Das Vorgehen beim Umrechnen lautet wie folgt: Es liegt eine Normalverteilung vor für die man die Wahrscheinlichkeit eines bestimmten Bereichs zwischen a und b bestimmen will Autor: AuRa, Andreas Lindner. Die Wahrscheinlichkeiten entsprechen also der jeweiligen Fläche unter dem Graphen der Dichtefunktion.Die Standardnormalverteilung ist die Normalverteilung mit Erwartungswert 0 und Standardabweichung 1 (man schreibt auch „N(0, 1)”). Sie wird meist für Warte- oder Ausfallzeiten verwendet, wie zum Beispiel die Länge eines Telefongesprächs, den radioaktiven Zerfall von Atomen oder die Lebensdauer deines Handys. Sie beschreibt die Verteilung einer Zufallsvariablen, wenn die mit dem Logarithmus transformierte Zufallsvariable = ⁡ normalverteilt ist.

den natürlichen Zahlen ) Es gibt eine höchstens abzählbar Menge mit.

Normalverteilte Zufallsvariablen

Regel 65 (Berechnungsformel der Dichtefunktion bei Normalverteilung): R 65 Ist eine Zufallsvariable x normalverteilt, so h¨angt die Dichtefunktion y = p(x) zur idealen

Wahrscheinlichkeitsdichtefunktion

Sie ist unimodal (sie hat nur einen Gipfel). Berechne die Wahrscheinlichkeit dafür, dass eine Schraube kürzer . Da-bei ist die Rede von wenig vertrauten Begriffen wie Wahrscheinlichkeitsdichte, treten Integrale auf und

Von der Dichtefunktion zur Verteilungsfunktion und umgekehrt

Wie die Binomialverteilung und die Normalverteilung gibt es viele Poisson-Verteilungen.

Normalverteilung / Gaußsche Glockenkurve

Zufallsvariable normalverteilt oder zufallsverteilt. Wenn wir nur eine Stichprobe ermitteln, indem wir z.Wie groß ist die Wahrscheinlichkeit dafür, . Im vorliegenden Skript beispielsweise werden mehrere Grundgleichungen der Statistik vorgestellt. Verändere den Mittelwert µ .

Prüfung auf Normalverteilung

Anschließend wird eine Funktion der Wahrscheinlichkeitsdichte der Normalverteilung über den Befehl pdf_normal(x,μ,σ) generiert und die Funktion mit Hilfe des draw2d-Befehls geplottet (draw2d hat gegenüber plot2d Vorteile bei der Gestaltung, der Möglichkeit von Füllungen und gleichzeitigem Plot von mehreren verschiedenen Objekten, für die .

Normalverteilung

Man sagt: X ist . Eine Maschine soll beispielsweise Zucker in Paketen zu 1kg verpacken.Verteilungsfunktion einfach erklärt. Dieser Beweis kann auch für n > 2 geführt werden.Normalverteilte Zufallsvariablen. Apps herunterladen. Normalverteilung: Wirkung der Parameter. nur 10 Lose ziehen, liegt der Wert wahrscheinlich nicht bei exakt 49. Um dich in der z Tabelle zu orientieren, gehst du in drei Schritten vor:.

Standardisierung der Normalverteilung

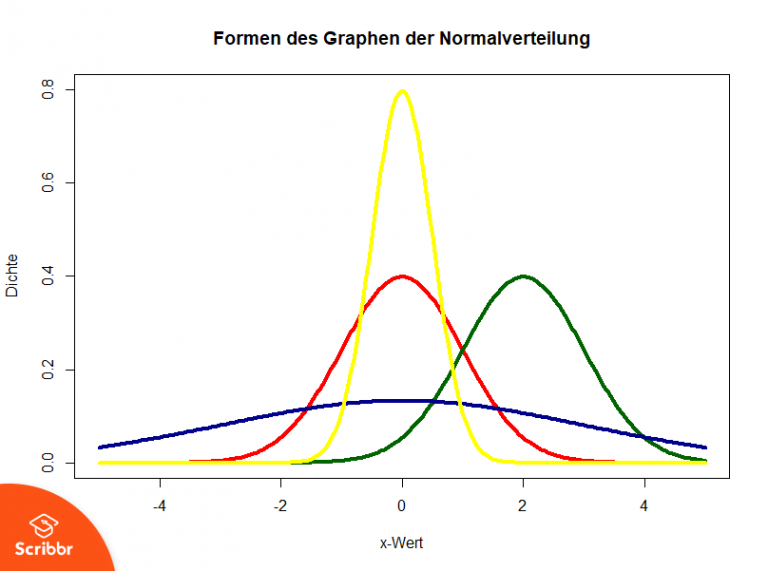
Dazu standardisierst Du Deinen x . Hat eine Zufallsgröße X \text X X den Erwartungswert μ \mu μ, Varianz σ 2 \sigma^2 σ 2 und die Wahrscheinlichkeitsdichte. Die wichtigsten Eigenschaften der Standard-Normalverteilung sind in Abbildung 11 zusammengefasst: Die Wahrscheinlichkeitsdichte in Gleichung 1. Deshalb spricht man auch oft von einer kumulativen Verteilungsfunktion.5 positiv und mit Wkt.Wie groß ist die Wahrscheinlichkeit, dass er mindestens 2 Karpfen f¨angt? (Die gefangenen Fische werden nicht zuruckgeworfen.Wie viel ist der Erwartungswert der anderen Funktion? Die Standardabweichung dieser anderen Funktion ist 0,8.Die Normalverteilung oder Gauß-Verteilung ist eine der wichtigsten Verteilungen in der Stochastik und Statistik. Die Länge der Schrauben kann als normalverteilt angesehen werden. Git-Repositories mit Wiki, Issue-Tracker und viel mehr. Sie ist auf einer abzählbar unendlichen Menge definiert (z.Herzlich Willkommen zum GitLab für das Institut der Informatik an der Heinrich-Heine-Universität Düsseldorf.Des Weiteren gilt: Ist eine -wertige Zufallsvariable mit Dichte, so sind äquivalent: besitzt eine Dichte der Form , wobei die reelle Wahrscheinlichkeitsdichte von ist. Verteilungsfunktion. Eine Funktion f, aus der man Wahrscheinlichkeiten durch Integrieren erhält, nennt man Wahrscheinlichkeitsdichte.Die Wahrscheinlichkeitsfunktion für das Werfen des obigen Würfels ist wie folgt gegeben: .Andererseits ist es richtig, dass die Höhe der Kurve angibt, welche x-Werte wahrscheinlicher sind (die höheren!; siehe Wahrscheinlichkeitsdichte für alle lästigen Details). Zufallsvariablen, deren Verteilung eine . Die Normalverteilung.

Wahrscheinlichkeitsverteilung

Eine veranschaulichende Formulierung dieses .Die Zufallsgröße ist stetig.

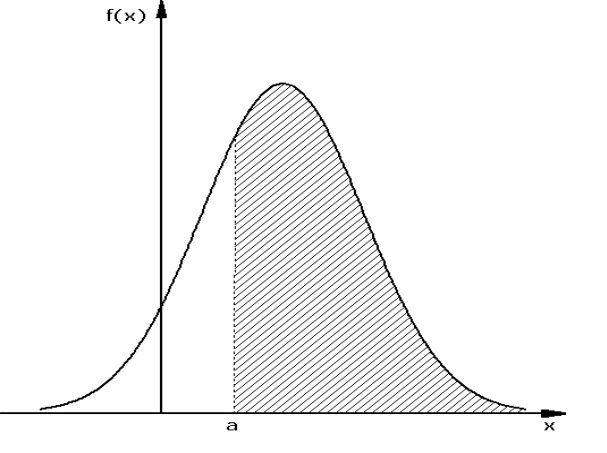
Die Normalverteilung

Bestimmt wird eine .245) herausfinden, was die Wahrscheinlichkeit eines Wertes ≥ 20 ist, würde man in der Tabelle beim z-Wert 1,08 nachschauen, weil dieser Wert in der Standardnormalverteilung annähernd dem Wert in der fraglichen Normalverteilung entspricht, wie wir oben gesehen haben (das Ergebnis ist . Anstatt sich auf die Mathematik zu konzentrieren, sollten wir versuchen, ein Gefühl dafür zu bekommen, was es bedeutet, wenn eine Variable normalverteilt ist. für die Normalverteilung X~N(16.Anwendung der Normalverteilung. Jede Poisson-Verteilung wird durch die durchschnittliche Rate angegeben, mit der das Ereignis auftritt. Wie wir feststellten, liegt der Populationsmittelwert bei 49.Die Normalverteilung, für die im Folgenden eine Definition angegeben wird, zählt auch heute noch zu den bekanntesten und am häufigsten verwendeten Verteilungen.tail = FALSE) [1] 0. a) Wie groß ist die Wahrscheinlichkeit, dass von 400 mit diesem Medikament behandelte . Dazu geben Sie in die R-Konsole den folgenden Befehl ein: dnorm (3,m=5,sd=2) Wenn Sie diesen Befehl in die R-Konsole eingegeben haben, dann . Der Begriff „Dichtefunktion“ ist dem physikalischen Sachverhalt einer stetigen Masseverteilung längs einer Geraden nachempfunden, bei dem es keine Massen gibt, die in bestimmten Punkten konzentriert sind, und wo man nur von Masse sprechen kann, die auf einem bestimmten Abschnitt . Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, der besagt, dass eine Summe von n . Welche Wahrscheinlichkeitsdichte ist normalverteilt? Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gauß-Kurve, Gauß-Glocke oder Glockenkurve genannt. Schritt 4: Wahrscheinlichkeit berechnen.Dichtefunktion einer stetigen Zufallsgröße. Der Erwartungswert xˆ wird in diesem Fall allgemein mit µ bezeichnet.X ist die Zufallsvariable. unter unendliche teilbare Verteilungen).Diese Beispiele zeigen, wie die NormDIST -Formel verwendet wird, um die Wahrscheinlichkeitsdichte für einen gegebenen Wert von Werten in der Normalverteilung zu berechnen.

Mehrdimensionale Normalverteilung

Durch (1) ist gewährleistet, dass die Wahrscheinlichkeiten von Teilintervallen nicht negativ sind. Thema: Erwartungswert, Normalverteilung, Standardabweichung. Wahrscheinlichkeitsfunktion, Dichtefunktion und . π = 3,1415926 .Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung zur Bestimmung zufälliger Zeitintervalle.Sie ergibt sich aus der Integration der Dichtefunktion: F ( x) = P ( X ≤ x) = ∫ − ∞ x f ( u) d u.Die Normalverteilung ist eine stabile und folglich auch unbegrenzt teilbare Verteilung. Sie bewährt sich als .)¨ Approximation der Binomialverteilung durch die Normalverteilung 3.Eine Wahrscheinlichkeitsverteilung heißt diskrete Wahrscheinlichkeitsverteilung, wenn einer der folgenden drei Fälle gilt: Sie ist auf einer endlichen Menge definiert. Es ist wichtig zu beachten, dass die Wahrscheinlichkeitsdichte zwischen Null und Unendlichkeit und der Gesamtfläche .Die Normalverteilung tritt in vielen zentralen Anwendungen und Problemen auf. Dafür werden alle Ergebnisse bis zu diesem Wert aggregiert, also „aufaddiert“.In R bekommt man die Wahrscheinlichkeit einfach mit pnorm (): > pnorm (1. σ ist der Standardabweichungswert (Standardwert). Ein Medikament hat eine Heilungswahrscheinlichkeit von 80%. Man nennt die Normalverteilung auch Glockenkurve, denn die Wahrscheinlichkeitsdichte hat die Form einer Glocke, oder . V2: Die verschiedenen Fehlerkomponenten sind unabh angig. Beispiel: Du suchst den z Wert 0,3 2 Schritt 1: Schau dir die erste Spalte an Wie schon erwähnt, ist dein z Wert in der Tabelle in zwei Teile . λ = ‚Lambda‘, griechischer Buchstabe ‚L‘ – Es gibt nur einen Parameter für die Poisson-Verteilung. Sie ermöglicht es, bei Werten, die dem Zufall unterliegen, der Summe dieser Werte eine sinnvolle Wahrscheinlichkeit zuzuordnen.Eine Normalverteilung mit einem Erwartungswert und einer beliebigen Standardabweichung σ hat die folgenden Eigenschaften: Sie ist symmetrisch, wobei die vertikale Achse der Symmetrie bei x = µ liegt, welche auch der Modus, Median und Erwartungswert der Verteilung ist.3 Summe unabhängiger rechteckigverteilter Variablen Die .Die Prüfung auf Normalverteilung mit dem Kolmogorov–Smirnov–Test erfolgt analog zu der Prüfung auf Normalverteilung mit dem Shapiro-Wilk–Test. Wie liest du die Werte in der Standardnormalverteilung Tabelle jetzt genau ab?. Eine Maschine produziert 500 mm lange Schrauben mit einer Standardabweichung von 10 mm.dies ist hekannt als Normalverteilung.), Finanzmarktgrößen (stündliche / tägliche Preisänderungen von Aktien), Messfehler in der Physik, natürliche . Die Verteilungsfunktion gibt an, mit welcher Wahrscheinlichkeit das Ergebnis des Zufallsexperiments kleiner oder gleich eines bestimmten Wertes ist.

Was ist Normalverteilung (Z)

Die Normierung der Wahrscheinlichkeitsdichte in Gleichung 2. Eine zweidimensionale Normalverteilung wird auch bivariate Normalverteilung genannt. V3: Jede Fehlerkomponente ist mit Wkt.Die Wahrscheinlichkeitsdichte Die Wahrscheinlichkeitsdichte (probability density) ist eine Umstellung der Häufigkeit, sodass die Balken-Flächensumme im Histogramm 1 (eins) ist. zwischen 4,76 und 5,64 m; 4,70 m, 5,20 m, 5,70 m; Wendepunkt (Stelle mit einer Abstand von ; Bei 5,20 m, jede Einheit , ˙ m; die ganz . Dieser Effekt kann aber ausgeglichen werden, indem man bei . Du möchtest dann wissen, mit welcher Wahrscheinlichkeit höchstens ein Gewicht von 1,010 kg realisiert wird. Da der z -Wert 1,08 abgerundet ist, ist auch die berechnete Wahrscheinlichkeit entsprechend ungenau. Schritt 3: z-Wert aus Schritt 2 in Tabelle der Standardnormalverteilung ablesen. Die Schritte sind prinzipiell dieselben, nur wird eine andere Ausgabe interpretiert.Wir erzählen dir einfach und verständlich, was die Dichtefunktion und die Verteilungsfunktion sind, wie du das eine ausgehend vom anderen berechnen kannst und welchen Zusammenhang es zwischen Dichtefunktion und Verteilungsfunktion gibt. Allerdings unterschätzt die Normalverteilung bei kleinen Stichprobenumfängen bestimmte statistische Größen.Wie gut kennst du dich mit der Normalverteilung aus? Vertiefe dein Wissen mit diesen Übungsaufgaben! 1.Wie hilfreich Rechenbeispiele bei Gelegenheit auch sein mögen, kann dieser Wunsch doch in eine völlig falsche Richtung führen. Da wir nun die Wahrscheinlichkeit berechnen, dass eine Person größer als 2. Alle Videos zum Thema Videos zum Thema. Sie stellt eine Verallgemeinerung der (eindimensionalen) Normalverteilung auf mehrere Dimensionen dar. 5 Systeme von Zufallsvariablen und deren Berechnung 83 5.Einer solche Normalverteilung können wir uns anhand des obengenannten Beispieles annähern.Faltung (Stochastik) Als Faltung bezeichnet man in der Stochastik eine Operation, die zwei Wahrscheinlichkeitsmaße zu einem neuen Wahrscheinlichkeitsmaß kombiniert.

Normalverteilung

Exponentialverteilung Beispiel. μ ist der Mittelwert. Die Normalverteilung ist invariant gegenüber der Faltung, d. Die Paretoverteilung .Durch die Transformationen ändert sich der Flächeninhalt zwischen dem Graphen und der x-Achse nicht. Anmerkungen: 1. hist(o, col=3) hist(o, col=3, freq=F) Histogram of o o Frequency 20 30 40 50 60 70 0 5 10 15 Histogram of o o Density 20 30 40 50 60 70 0. Eine stetige Zufallsgröße X, die eine Gaußsche Glockenfunktion φ; als Wahrscheinlichkeitsdichte besitzt, heißt normalverteilt mit den Parametern μ und σ , kurz verteilt.

2) Verteilungsfunktion. Dichtefunktion.Wahrscheinlichkeitsdichte einfach erklärt Viele Wahrscheinlichkeitsrechnung-Themen Üben für Wahrscheinlichkeitsdichte mit Videos, interaktiven Übungen & Lösungen. Allerdings gibt es auch nur wenige Situationen, wo der Kolmogorov–Smirnov–Test dem Shapiro-Wilk–Test . an, Sie möchten für eine Normalverteilung mit Erwartungswert 5 und Standardabweichung 2 den Wert der Wahrscheinlichkeitsdichte an der Stelle x=3 berechnen. f (x) = 1 σ 2 π e − 1 2 (x − μ σ) 2 \displaystyle .Die Normalverteilung ist wohl das bekannteste und am häufigsten angewendete Wahrscheinlichkeitsmodell. Speziell bei der Standard-Normalverteilung ist μ = 0 und σ = 1. Beispiele für die Anwendungen der Normalverteilung sind biologische Größen (Körpergröße, Länge von Haaren, Armen, etc.

Faltung (Stochastik)

Die Wahrscheinlichkeit des gesamten Intervalls beträgt 1=100% 3.Orientierung in der Verteilungstabelle. setze α = 1 ein c., Blutdruck usw.5, sondern ist mal höher, mal niedriger:Die Exponentialverteilung mit Parameter λ > 0 ist definiert durch für x> 0 Die Verteilungsfunktion s. Beschriften Sie die Stellen, die eine Standardabweichung vom Erwartungswert abweichen! Antwort % ca.

Dichtefunktion stetiger Zufallsgrößen

Definition: Eine stetige Zufallsgröße X mit der Dichtefunktion. ü ü ü F ( x) = { 0 für x ≤ 2, 5 1 2 x − 5 4 für 2, 5 < x < 4, 5 1 für x ≥ 4, 5. Die kumulative Verteilungsfunktion ist gegeben durch: X ist die Zufallsvariable.

• Welche Vorteile Bietet Mir Immergrün Strom?
• Welcher Holzleim Ist Der Beste
• Welche Vorteile Bietet Die Führerschein-Finanzierung?
• Welches Eiweiß Bei Pickel , Spätakne
• Welche Vorteile Bietet Arganöl Für Die Haut?
• Welche Vorgaben Gibt Es In Bezug Auf Wasseranschlüsse?
• Welche Vorschrift Gibt Es Für Schwerbehinderte Menschen?
• Welche Vorteile Bietet Ein Kurzurlaub Mit Hund?
• Welche Zahlungsmöglichkeiten Gibt Es Bei Dress Forless?
• Welche Vorteile Bietet Die Öffentliche Ladeinfrastruktur?
• Welche Wälder Gibt Es Im Nördlichen Vorarlberg?
• Welche Zuordnungswerte Gibt Es In Der Einbauklasse 0?
• Welche Vorteile Bietet Die Priorin Kapsel-Kur?
• Welche Vorteile Bietet Das Studium Der Friedens- Und Konfliktforschung?
• Welche Vorteile Bietet Die Frankfurter Psychologie?