Was Ist Eine Quadratische Funktion?

Di: Samuel

Wir hatten uns bereits die Einführung zu den quadratischen Funktionen angeschaut sowie die Normalparabeln.

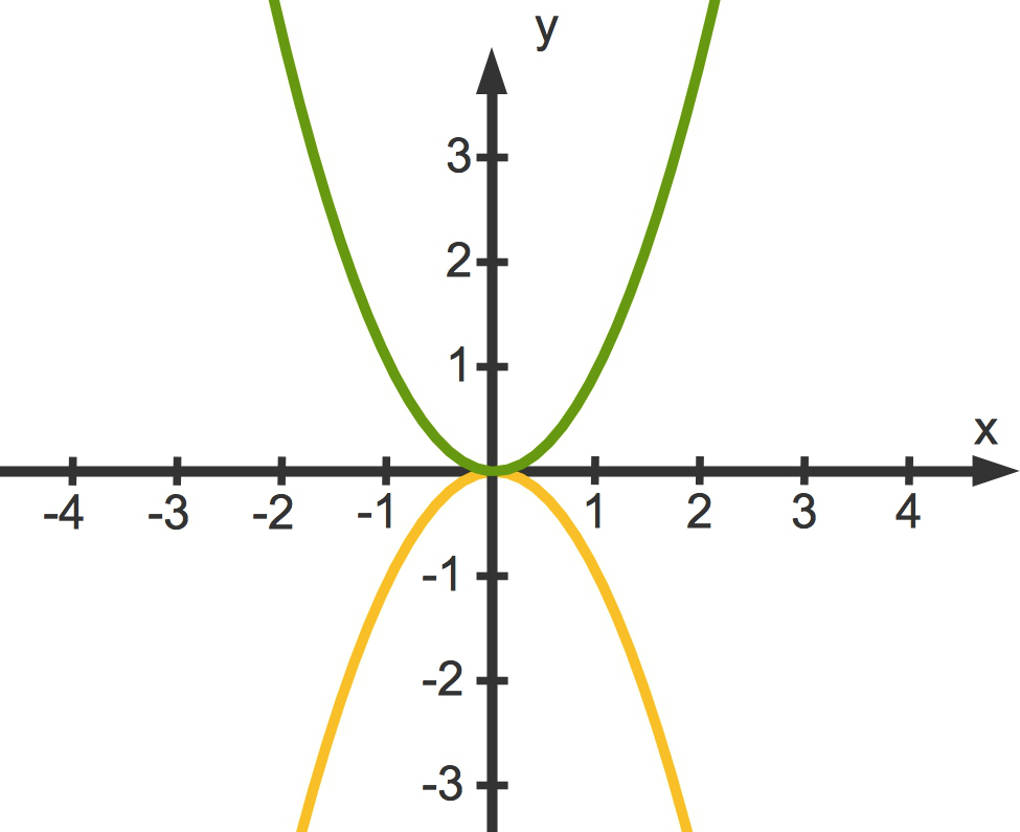
Quadratische Funktionen: f(x) = a · x² online lernen

Die y-Achse ist die Symmetrieachse der Parabel. Gut zu wissen . f ( x) = a x 2 + b x + c.Quadratische Funktionen werden im Allgemeinen durch die Funktionsgleichung f (x) = ax² + bx + c (a, b, c, x ˘ ˇ; a ≠ 0) beschrieben. Häufig wird auch nach der Funktionsgleichung einer quadratischen Funktion gefragt.Eine Funktion f ist eine Beziehung zwischen zwei Mengen — der Definitionsmenge () und der Wertemenge (). (01:53) Um den Funktionswert zu berechnen, musst du den x-Wert in den Funktionsterm einsetzen und dann das Ergebnis ausrechnen: Beispiel: Du sollst den Funktionswert für den Term f ( x) = 2 x + 3 an der Stelle x = 4 berechnen.Eine Funktion mit einer Gleichung der Form. Existiert eine inverse Matrix, so ist diese ebenfalls invertierbar. (00:13) Ganzrationale Funktionen oder Polynomfunktionen, werden stets in Abgrenzung zu den gebrochen rationalen Funktionen definiert. Die linke Seite dieser Gleichung ist der Term einer quadratischen Funktion (allgemeiner ausgedrückt: ein Polynom zweiten Grades) () = + +; der Funktionsgraph dieser Funktion im kartesischen Koordinatensystem ist eine . das b gibt direkt die Steigung des Funktionsgraphen im Schnittpunkt mit der y-Achse an. Außerdem hast du gelernt, wann eine quadratische Funktion nach oben oder unten geöffnet ist. Beide Wörter stehen also für die gleiche Art von Funktionen.

Lösungsmenge • Was ist eine Lösungsmenge? · [mit Video]

proportionale Funktionen, lineare Funktionen, quadratische Funktionen oder Exponentialfunktionen. Da die p-q-Formel nicht lösbar ist, gibt es kein Ergebnis und somit auch keine reellen Nullstellen. Wie oben bereits beschrieben, ist eine quadratische Funktion nicht monoton und hat keine allgemeine Umkehrfunktion.Nullstellen quadratische Funktion Beispiele. Binomische Formel oder 2.Lerne mit 58 Transformation von Funktionen Karteikarten in der kostenlosen StudySmarter App.Gleichungen mit einer nichtleeren Lösungsmenge nennst du lösbar. Im Lerntext Wie verschiebt man eine Normalparabel kannst du nachlesen und lernen, wie du eine Normalparabel verschiebst. und höheren Grades Dauer: 05:02 Umkehrfunktion Dauer: 04:19 Verkettung von Funktionen Dauer: 03:48 Schnittpunkt .

Ganzrationale Funktionen • Polynomfunktionen · [mit Video]

Für den Wertebereich quadratischer Funktionen ist das aber nicht der Fall. Liegt a zwischen 0 und 1 bzw.Schau dir die Schritte gleich an einem konkreten Beispiel für eine quadratische Gleichung an: 2×2 – 4x = 30. Im Rahmen der quadratischen Ergänzung wird der Term so umgeformt, dass die 1.Jetzt weißt du auch schon, wie eine Funktion gestreckt und gestaucht wird. Der Punkt an dem die Parabel ihr Minimum annimmt heißt Scheitelpunkt. Die Allgemeinform einer quadratischen Funktion ist: f (x) = a·x² + b·x + c, wobei a, b und c reelle Zahlen sind und x die Variable. Ist die Parabel nach unten geöffnet, ist die Wertemenge . Die Bezeichnung der Polynomfunktionen als ganzrationale Funktionen soll diese Funktionsgruppe von den sogenannten gebrochenrationalen Funktionen abgrenzen. Eine quadratische Funktion ist eine ganzrationale .

Transformation von Funktionen

Die Scheitelpunktform ist eine spezielle Form einer quadratischen Funktion, aus der man den Scheitelpunkt der zugehörigen Parabel direkt ablesen kann. zur Stelle im Video springen.Quadratische Funktionen. In diesem Video wird gezeigt, wie man die Nullstellen verschiedener quadratischer Funktionen findet. Bei lösbaren Gleichungen kannst du noch zwischen teilgültigen und allgemeingültigen Gleichungen unterscheiden. Dazu wird zunächst grafisch kurz erklärt, was eine Nullstelle überhaupt ist und wie man eine Parabel verschieben kann. Schritt 1: Forme die Gleichung so um, dass auf einer der beiden Seiten die Null steht.Funktionsgleichung von quadratischen Funktionen aufstellen.Quadratische Funktionen – Lösungen der Aufgaben. Teste dein neu erlerntes Wissen mit unseren Übungsaufgaben. Du setzt also die 4 für x in die Funktionsgleichung ein: f ( 4) = 2 · 4 + 3 = 8 + 3 = 11. (01:14) Willst du bei einer quadratischen Funktion die Wertemenge bestimmen, geht das ganz einfach: Bringe die Funktion dafür einfach in die Scheitelpunktform f (x) = a • (x – d)2 + e.

oder einer Gleichung, die durch äquivalentes Umformen in diese Form überführt werden kann, heißt quadratische Funktion.Quadratische Funktionen besitzen eine Spiegelachse. Der Schnittpunkt der Parabel mit ihrer Symmetrieachse wird Scheitelpunkt genannt.Da die y -Koordinate eines Schnittpunktes mit der x -Achse immer Null ist, lautet der Ansatz zur Berechnung einer Nullstelle: y = 0 . Woher ich das weiß: Hobby – . f(x) = a x 2 + b x + c Hier sind a, b und c beliebige Zahlen, wobei a nicht 0 sein darf. Andernfalls heißt sie singulär.

Quadratische Gleichung

Die allgemeine Gleichung einer solchen Funktion lautet: f (x)=ax^ {2}+bx+c f (x)= ax2 + bx +c. Dabei gilt: D>0: zwei Lösungen, D=0: eine Lösung, D<0: keine Lösung.Der Graph einer quadratischen Funktion wird Parabel genannt. Dazu gibt es verschiedene Abwandlungen der Form f (x) = ax² + bx + c, aber dazu später mehr.Die Diskriminante D ist der Ausdruck unter der Wurzel der Mitternachtsformel (auch abc-Formel ) beziehungsweise der pq-Formel. Eigenschaften quadratischer Funktionen bestimmen. Für die Definitionsmenge $ \mathbb{D}$ einer Funktion $f(x)$ können grundsätzlich alle $x$-Werte angenommen werden und damit ist diese auf ganz $ \mathbb{R}$ definiert. Eine Parabel ist immer symmetrisch, dabei verläuft die Symmetrieachse parallel zur $y$-Achse.Was ist eine Funktion? Quadratische Funktionen; Einordnung . Sie verläuft parallel zur y y -Achse durch den Scheitelpunkt. Eine lineare Funktion $f(x)$, ist eine ganzrationale Funktion ersten Grades, welche grafisch durch eine Gerade dargestellt wird. f(x) = x2 − 4x + 5. 0 und -1, dann ist die Parabel breiter als die Normalparabel. Die allgemeine Form ist. Ist a 0, dann ist die Parabel nach oben geöffnet. p-q-Formel anwenden. Die vier einfachsten Möglichkeiten, eine Funktion algebraisch zu transformieren, sind:

Quadratische Funktion

Im Anschluss werden zahlreiche Beispiele vorgerechnet:

Nullstellen berechnen • Nullstelle bestimmen, Nullstellen

Diese besondere Form nennen wir auch die Normalparabel. Quadratische Funktion – allgemeine Form.Als quadratische Funktionen bezeichnen wir Funktionen, bei denen die höchste Potenz, in der die Variable x x vorkommt, das Quadrat ist (also x^ {2} x2 ). Beispiele für Terme mit quadratischer Variable.Eine quadratische Funktion ist ein Polynom zweiten Grades, also eine Funktion der Form: \boldsymbol f\boldsymbol(\boldsymbol x\boldsymbol)\boldsymbol=\boldsymbol a\boldsymbol x^\mathbf2\boldsymbol+\boldsymbol b\boldsymbol x\boldsymbol+\boldsymbol c mit \;\;a\neq0\\ Der Graph einer quadratischen Funktion ist immer eine Parabel .Mit der Parabel Formel kannst du quadratische Funktionen aufschreiben:.So jetzt weißt du, was eine quadratische Funktion ist und wie du sie zeichnen kannst. Die meisten Funktionsterme enthalten zusätzlich Koeffizienten, die auch Parameter genannt werden.Eine inverse Matrix ist nur für quadratische Matrizen definiert.Bei der quadratischen Funktion handelt es sich um eine Kurve mit der Funktionsvorschrift y = x² oder f (x) = x².

Transformation von Funktionen: Übersicht

Es existiert aber nicht für jede quadratische Matrix eine inverse Matrix. Eine quadratische Funktion ist ein Polynom vom Grad 2. Das wichtigste Merkmal von quadratischen Funktionen ist, dass der höchste Exponent der Variablen den Wert 2 2 hat. Die einfachste Form . Polynomfunktionen sind – wie der Name bereits sagt – immer die Summe einzelner polynomieller Bestandteile in einer Variablen . Die allgemeine Form einer quadratischen Funktion lautet wie folgt: f (x)=ax^2+bx+c f (x) = ax2 +bx +c. Um die Nullstellen einer Funktion f zu berechnen, suchst du die x-Werte, für die f (x) = 0 wird. Bestimmung von p und q. Hier ist eine ausführliche Erklärung: Eine quadratische Funktion ist eine mathematische Funktion, die durch eine Gleichung der Form f (x) = ax^2 + bx + c f (x)= ax2 +bx+c . y=f (x)=ax^2+bx+c y = f (x) = ax2 + bx + c, wobei a\neq 0 a =/ 0 vorausgesetzt wird, da die Funktion sonst zu einer linearen Funktion entartet. Viel mehr kann man damit nicht direkt erkennen.Was ist eine Umkehrfunktion und wie berechnest du eigentlich Schnittpunkte? Das erfährst du hier! Karriere starten bei Funktionsgleichung Dauer: 04:33 Nullstellen berechnen Dauer: 04:21 Nullstellen ganzrationaler Funktionen 3.Eine quadratische Gleichung ist eine Gleichung, die sich für den univariaten Fall in der Form + + = mit schreiben lässt .

Quadratische Funktionen: Aufgaben mit Lösungen

Wenn du den Parameter a veränderst, kannst du den Funktionsgraphen strecken oder stauchen. a bestimmt die Öffnung der Parabel. Hier gibt es verschiedene Möglichkeiten, wie du die Funktionsgleichung aufschreiben kannst: f(x) = ax 2 + bx + c a llgemeine Form

Eigenschaften quadratischer Funktionen bestimmen

Mithilfe der quadratischen Ergänzung kann man jede Parabelgleichung auf die Form einer binomischen Formel . Zeichnest du den Graphen der Parabelgleichung, erhältst du eine Parabel. Eine ganzrationale Funktion zweiten Grades und lässt sich innerhalb des Koordinatensystems durch eine Parabel darstellen und bezeichnet quadratische . Dabei nennt man das quadratische Glied, bx das lineare Glied und c das absolute Glied der Funktionsgleichung. Eine Funktion f mit der Funktionsgleichung. Beispiel für eine quadratische Funktion: y =x2 .

Nullstellen (Quadratische Funktionen)

Eine Matrix A heißt invertierbar, falls sie eine inverse Matrix A-1 besitzt. Es handelt sich hierbei um eine Zuordnung, bei der wir der . Bevor wir uns die Scheitelpunktform anschauen, wiederholen wir kurz, was die allgemeine Form eine quadratische Funktion ist. Es handelt sich um eine gerade Funktion, .

Quadratische Funktionen zeichnen

Quadratische Funktion strecken, stauchen & spiegeln

−1−−−√ → im Bereich der reellen Zahlen nicht berechenbar. Die einfachste quadratische Funktion (a = 1, b = c = 0) hat die Funktions gleichung f (x) = x². „Allgemeinform“ kennen. Das Quadrat der Variable x x ist x^ {2} x2. Die Diskriminante sagt dir, wie viele Lösungen eine quadratische Gleichung besitzt. Identifiziere die dazugehörige richtige Aussagen.

Punktprobe (Quadratische Funktionen)

Eine quadratische Funktion ist eine Funktion, die als Funktionsgleichung die Gleichung der Form (allgemeine Form) y = ax2 + bx + c. Selten steht die Variable allein. Sie kann eine oder mehrere Zahlen enthalten. Dabei darf der Parameter a nicht den Wert Null besitzen (a ≠ 0). Ist der Graph einer quadratischen Funktion gegeben, ist die Sache ziemlich einfach: Wir erkennen, dass der Punkt $\text{P}_2$ (im Gegensatz zum Punkt $\text{P}_1$) auf der Parabel liegt. Im folgenden Lerntext bearbeiten wir eine realitätsnahe Textaufgabe zum Thema quadratische Funktionen. Merke: Die Scheitelform ist ein Versuch, eine quadratische Funktion als „binomische Formel mit Rest“ zu interpretieren. Ist die Parabel nach oben geöffnet, ist die Wertemenge [e; ∞ [. Dafür setzt du die Funktion gleich 0 und löst die Gleichung nach x auf. Zunächst musst du also einen Definitionsbereich für die Umkehrfunktion festlegen. f ( x) = a ( x − d) 2 + e. Eine Parabel kann bis zu zwei .

Quadratische Funktion

Der Begriff ganzrationale Funktion ist eine andere Bezeichnung für eine Polynomfunktion. Wir nehmen als Beispiel die Funktion . Wenn c < 0, dann gilt: Graph wird nach links verschoben. Wir wollen wissen, ob ein Punkt auf dem Graphen einer quadratischen Funktion liegt.In der Regel gilt für quadratische Funktionen: das b x steht da, um jede quadratische Funktion in ausmultiplizierter Form darstellen zu können und nicht nur quadratische Funktionen mit der Extremstelle x = 0.Wertebereich – quadratische Funktionen. Damit bringst du die quadratische Gleichung in die allgemeine Form. Wir wünschen dabei viel Spaß!

Funktionsgleichung • bestimmen an Beispielen

Eine Funktionsgleichung ist so aufgebaut, . Wichtig ist dabei, dass jedem Element x aus der Definitionsmenge ( Argument ) genau ein Element y aus der Wertemenge ( Funktionswert) zugeordnet wird (z.Die Transformation von Funktionen können wir aus zwei Blickwinkeln betrachten: Der Funktionsterm verändert sich (Algebraischer Blickwinkel) Der Funktionsgraph verändert sich (Geometrischer Blickwinkel) Algebraische Transformationen . Der Definitionsbereich einer quadratischen Funktion umfasst alle -Werte, für die der Funktionsterm definiert ist. Aus der Scheitelpunktform lässt sich der Scheitelpunkt leicht ablesen: S ( d | e). 0 = x2 − 4x + 5.

Was sind quadratische Funktionen?

Enthält sie nur eine Zahl, nennt man die Gleichung auch eindeutig lösbar. Hierbei zeigen wir Schritt für Schritt, wie du solche Textaufgaben zu .Quadratische Funktionen sind Funktionen, in denen die höchste Potenz von das Quadrat ist.

Man nennt ax^ {2} ax2 das quadratische Glied, bx bx das lineare .Analog funktioniert das Ganze natürlich auch, wenn du die Normalform in Scheitelform umrechnen möchtest. Eine Funktion f ( x) wird in x-Richtung um c-Einheiten verschoben und damit ergibt sich eine neue Funktionsgleichung g ( x) = f ( x − c).Eine Funktionsgleichung ist eine Gleichung, die eine eindeutige Zuordnung beschreibt.In diesem Video schauen wir uns zum ersten Mal eine quadratische Funktion.Ganzrationale Funktionen einfach erklärt.Eine quadratische Funktion ist allgemein durch folgende Form gegeben: f (x)=ax^2+bx+c f (x) = ax2 +bx+c. Der Graph einer quadratischen Funktion ist eine Parabel. Der Graph der Funktion mit der Gleichung f (x) = x² heißt Normalparabel. Außerdem lernst du dort, . x y = 2 · x ). Unterschiedliche Fälle der Diskriminante.Lineare Funktionen und quadratische Funktionen. Eine Parabel kann sowohl nach oben als auch nach unten geöffnet sein. Die Nullstelle x0 einer Funktion ist die Stelle, an der ihr Graph die x-Achse schneidet. heißt quadratische Funktion.Quadratische Funktionen (Parabeln) Der Graph einer quadratischen Funktion ist eine Parabel. Alle Punkte P (x|y), deren Koordinaten x und y die Gleichung erfüllen, liegen auf der Parabel. Quadratische Funktionen besitzen entweder keine, eine oder zwei Nullstellen. Um die pq Formel anwenden zu können, darf vor dem x2 jedoch kein Vorfaktor stehen.Der Unterschied zwischen einer quadratischen Funktion und einer quadratischen Gleichung liegt hauptsächlich in ihrem Konzept und Verwendungszweck. Neben der allgemeinen Form gibt es noch eine weitere Form, die uns hier beschäftigen wird: Scheitelpunktform. Zum Beispiel kannst du f(x) nur für positive Werte betrachten. Im Beispiel formst du also 2x – 3 = 0 nach .

Wertemenge • einfach erklärt! · [mit Video]

Quadratische Funktionen in Mathematik

Die quadratische Ergänzung ist ein Verfahren zum Umformen von Termen, in denen eine Variable quadratisch (z. Der Graph der Funktion ist eine Parabel, die für a>0 a > 0 nach oben geöffnet . Die Normalparabel untersuchen. zu 2) Wenn du weißt, wie man quadratische Gleichungen löst, kannst du auch die Nullstellen quadratischer Funktionen berechnen. Die Scheitelpunktform einer quadratischen Funktion hat die Form: y = a ⋅(x + d)2 + e.

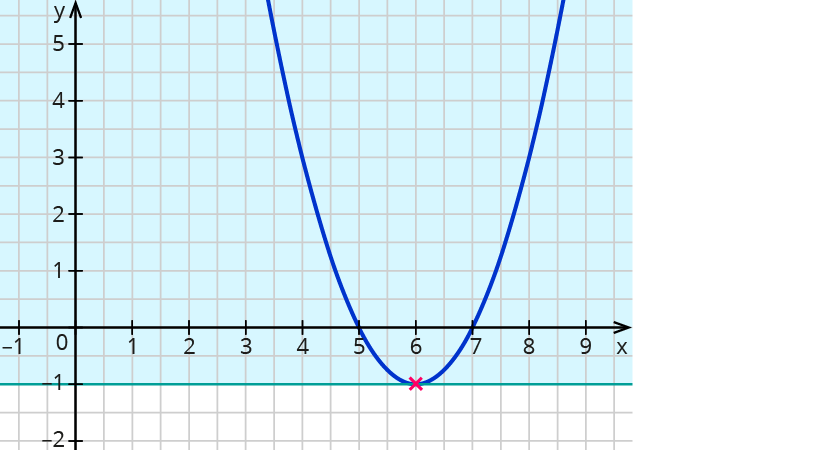
Eigenschaften quadratischer Funktionen bestimmen – kapiert.de

Wenn du die Vorzeichen von f (x) und/oder x änderst, kannst du die Funktion auf verschiedene Arten spiegeln. Der Graph einer quadratischen Funktion ist eine gekrümmte Kurve und heißt Parabel. Definitions – und Wertemenge einer Funktion. Hier erfährst du, was die Variablen a, b und c bedeuten. Dabei darf der Parameter a a nicht Null sein. Ihr Funktionsgraph ist immer eine Parabel .Nullstellen berechnen einfach erklärt. Anhand der Funktionsgleichung können wir verschiedene Arten von Funktionen unterscheiden, z. Wir schauen uns y=x^2 an. Die Parabel ist nach oben oder nach unten offen und nach links und rechts unbegrenzt. Quadratische Funktionen beschreiben.zur Stelle im Video springen. Quadratische Gleichung gleich null setzen. Ein wesentlicher Unterschied zur linearen Funktion ist, dass du für jeden y-Wert (außer dem des Scheitelpunkts) zwei x-Werte erhältst. Eine quadratische Funktion ist eine ganzrationale Funktion vom Grad 2 2.Verschiedene quadratische Funktionen. Der Graph einer quadratischen Funktion ist immer eine Parabel, verläuft also in einer Art U-Form.Um sie zu ermitteln, können wir die Scheitelpunktform der quadratischen Funktion bestimmen. Veröffentlicht: 11. Wegen y = f ( x) kann man auch f ( x) = 0 schreiben. Im Folgenden lernen wir die allgemeine Form bzw.Quadratische Funktion.

Quadratische Funktionen • Parabel, Funktionsgleichung · [mit Video]

WIKI Quadratische Funktionen der Funktionsklassen

BAHTMZ

General