BAHTMZ

Was Gilt Für Die Fourier-Koeffizienten?

Di: Samuel

Die letztere Aussage gilt allerdings nur für Funktionen mit c 0 =0. und Addition der Gleichungen ergibt Gesucht wird die reelle und . Oh, eine Aufgabe wie diese ist auch für mich interessant.

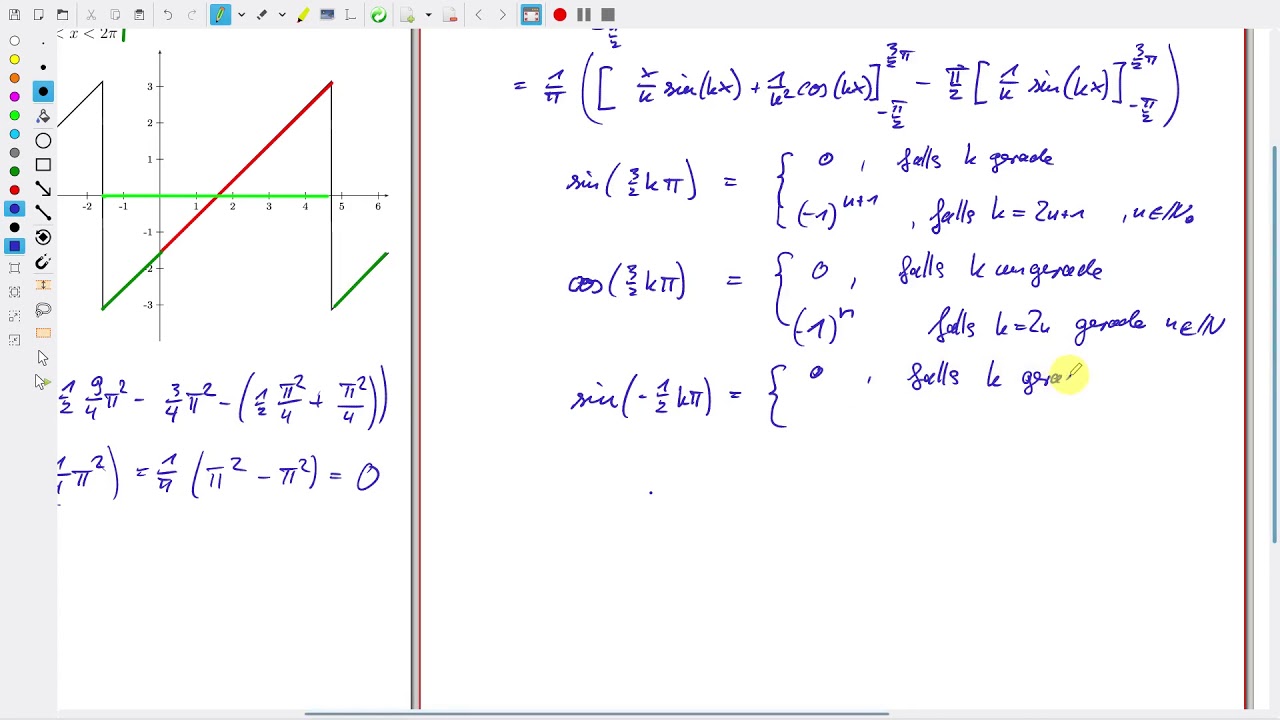
Beispiel: Fourier-Reihe der 2ˇ-periodischen Fortsetzung der geraden Hutfunktion x 2 0 2 f(x) = (ˇ+ x; x 2[ ˇ;0) ˇ x; x 2[0;ˇ) reine . Dabei ist die Grundfrequenz und die Grundkreisfrequenz mit . An einem einfachen Beispiel erläutern wir die Vorgehensweise für die Gleichung der schwingenden Saite.Ihre Fourier-Transformation berechnet sich gemäß.

Fourier Koeffizienten einer Funktion

Unterabschnitt Fourier-Koeffizienten umschalten . 2 Fourier-Basis. Zur Synthese dieser Funktion sind deshalb ebenfalls nur gerade Funktionen notwendig, also nur Cosinusfunktionen. Normalerweise werden Objekte und Koeffizienten in der gleichen Reihenfolge indiziert, sodass sich Ausdrücke wie + + + ergeben, mit als dem Koeffizienten der Variablen für jedes =,,, .Ist die 2π-periodische Funktion f(x) eine gerade Funktion, (d. auch direkt ausrechnen.

Phasenspektrum (Fourier)

Die Amplituden der erzeugenden Kreisfunktionen ergeben sich aus den Fourierkoeffizienten.In Teil 3 haben wir gesehen, dass wir ein periodisches Signal s mit Periodendauer T als Summe rotierender Zeiger . Tatsächlich ist aber eines der wichtigsten Anwendungsgebiete der Fourier-Transformation die Integration von Differentialgleichungen.

Fourier-Reihen

Die Fourier-Koeffizienten der Ableitung einer Funktion erhält man also, . Sie hat nicht nur die Entwicklung von Mathematik und Physik grundlegend gefördert, sondern besitzt bis heute zahlreiche Anwendungen in Naturwissenschaften und Technik. Eine Fourierreihe ist eine Darstellung einer periodischen Funktion als Reihe von Sinus- und Kosinusschwingungen verschiedener Frequenzen. Zusammenhang komplexer und reeller Fourier-Reihen 1-2.Zuerst multiplizieren wir Q (x) aus: Q (x)=a (x-1)+2b=ax-a+2b.Der Ausdruck unter dem Integral besitzt für alle k die obige intergrierbare Majorante.Dies folgt aus einer grundlegenden Eigenschaft der Exponentialfunktion, die für beliebige Zahlen z gilt: Gleichung . Art) (Beispiel: Rechteckfunktion 2), gilt: (32) Ist die . der Graph der Funktion ist achsensymmetrisch zur u-Achse (Ordinate) und es gilt u(t) = u(−t). Da Sinusfunktionen immer ungerade sind, sind deren Koeffizienten .Ich weiß nicht, wie ich an die Aufgabe rangehen soll. Das sind aber noch nicht alle Koeffizienten. Besten Dank schonmal für Eure Mühen! 20. Die Koeffizienten einmal sind die Zahlen vor der Unbekannten x.Damit können wir nun die Übersetzung ins Komplexe durchführen.

was ist ein koeffizient? (Mathematik)

Für die Fourier Koeffizienten gilt, dass sie für \(k \to \infty \) gegen Null konvergieren, gleichzeitig geht auch der Restfehler . Das heißt, dass die Variable mit dem Koeffizienten multipliziert wird und dadurch bestimmt, wie oft diese Variable vorkommt. Für die Funktionen sin(nx) hingegen würden wir mit n = 0 lediglich die konstante Funktion 0 bekommen. 4 Orthogonalitätsrelationen.Fourierreihen können zur Lösung partieller Differentialgleichungen benutzt werden.Kostenloser Fourier-Reihen-Rechner – Finden Sie die Fourier-Reihen von Funktionen Schritt für SchrittBeispiele für wichtige mathematische Koeffizienten: Koeffizienten des Polynoms, insbesondere der Leitkoeffizient Binomialkoeffizient Taylor-Koeffizienten (siehe Taylor-Reihe) Fourier-Koeffizienten (siehe Fourier-Reihe) Koeffizienten einer Potenzreihe oder Laurentreihe, hier insbesondere das Residuum Clebsch-Gordan-Koeffizient . Tolle Antwort !?? Kommentiert 1 . Die Datenaufnahme erfolgt mit einem USB-Oszilloskop der Firma Vellemann . b k = 0, für alle k), so sind die Fourierkoeffizienten c k reell.

Fourier-Reihen von geraden und ungeraden Funktionen

Der Ansatz ist wieder vergleichbar mit dem Versuch der Entwicklung einer Funktion in eine Potenzreihe: Wenn es geht, dann so. was hier zu beachten ist. Die Fourier-Reihe ist genau dann reell, wenn gilt.Für die Koeffizienten gelten dabei die Umrechnungsformeln bzw.Die Mathematik hinter dieser Zerlegung ist dabei das Berechnen der Fourierkoeffizienten zu den Grundschwingungen. Ist Y=DFT(y) mit einem weiteren Vektor , so gilt die Parsevalsche Gleichung für Fourier-Koeffizienten: Interpretationen der DFT

Fourier-Transformation

Wir stellen nun die Berechnungsformeln für die Koeffizienten an die Spitze.

Zusammenhang zwischen den Koeffizienten einer quadratischen

Ist f(x) eine reellwertige Funktion, so . Definition: Die Fourierreihe eines periodischen Signals x(t) lautet wie folgt: x(t) = A0 + ∞ ∑ n = 1An ⋅ cos(nω0t) + ∞ ∑ .Für eine nullpunktsymmetrische Funktion f (t) erhält man die Fourier-Koeffizienten: (30) Hat die Funktion die Eigenschaft der Halbwellensymmetrie (1. Für die Funktion f(x) = x mit der Periode T = 1 sollte ich a0 = 1, an = 0 und bn = − 1 2 ⋅ n ⋅ π erhalten. Da die Rechteckfunktion gerade.

Fourierreihe

Der direkteste und eleganteste Weg, die passenden Fourier-Koeffizienten zu einer gegebenen Funktion F zu finden, besteht darin, die Orthogonalitätsrelationen der trigonometrischen Funktionen auszunutzen, die für Sinus-Funktionen von der folgenden Form sind: (10) Analoge Relationen gelten für die Kosinus-Funktion.08) gilt allerdings: (f ∗δ k) −→ f bezgl. Analytisch betrachtet liegt das daran, dass einerseits die Folge der 2. Des Weiteren gilt nach dem Satz von . Einfaches Beispiel: . Reihe sehr viel schneller gegen 0 konvergiert, da 1 (2l 1)2 ˝ 1 n und darum die ersten Terme bei g eine größere Rolle spielen als bei f. Mit WolframAlpha habe ich es bereits versucht, egal was ich eingebe, es kommt immer etwas Komisches raus, oder nicht das . stehen ein Universal-Funktionsgenerator sowie ein Funktionsgenerator der Firma Rigol (Modell DG1012) zur Verfügung. Diese Verschiebungen und Streckungen, die bei einer Veränderung von entstehen, charakterisieren die Position und Form einer Parabel.Jede periodische Funktion x(t) kann in allen Bereichen, in denen sie stetig ist oder nur endlich viele Sprungstellen aufweist, in eine trigonometrische Reihe entwickelt werden, die man als Fourierreihe bezeichnet. der Antisymmetrie des Sinus ist also Für reelle Koeffizienten gilt d.Definition Fourierreihe.2 Komplexe Fourier-Koeffizienten. Satz (komplexe Darstellung einer reellen Fourier-Reihe) Für alle a, b ∈ ℝ gilt: a cos (k x) + b sin (k x) = a − i b 2 e i k x + a + i b 2 e −i k x.Wir stellen im Folgenden die wichtigsten dieser Regeln zusammen: Sätze und Regeln zu Fourierkoeffizienten bzw.Formeln für die Berechnung der fourierschen Koeffizienten. Alle neuen Fragen Sei f eine 2π-periodische Funktion, zeige dass die Funktion die Fourier-Koeffizienten c_{k}(g)=e^{-ika}c_{k}(f) hat

Eulersche Gleichungen für Fourier’sche Reihenentwicklungen

• In allen kompakten Intervallen [a,b], in denen f(t) stetig ist, ist die Konvergenz der Fourier-Reihe gleichmaßig. Dann heißen die in (2) und (3) definierten Zahlen die Fourier-Koeffizienten von f f. In der Mathematik ist ein Koeffizient ein Faktor, der zu einem bestimmten Objekt wie einer Variablen oder einem Basisvektor gehört. Die Fourier-Reihe ist genau dann reell, wenn c k = c k. Wir müssen daher nur die Koeffizienten an bestimmen.

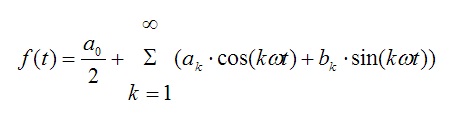
Wir schildern diese Berechnung der Fourierkoeffizienten und stellen so periodische Funktionen aller Couleur als .Berechnen Sie die Fourier-Koeffizienten der 2π-periodischen Funktion f(x) = x • cos(x) x = [0.In die Seitenleiste verschieben Verbergen. Nach dem Konvergenzsatz von Lebesgue konvergiert dieser also punktweise für k → ∞.Fourier-Koe zienten, da die entsprechenden Integrale aus Symmetriegr unden null sind bzw.F ur die Koe zienten gelten die Umrechnungsformeln a 0 = 2c 0; a k = c k + c k; b k = i(c k c k) bzw.Die dargestellte Funktion ist eine gerade Funktion, d. Darüber hinaus . Für reellwertige Funktionen ist des Weiteren eine Darstellung der Fourierreihe in der Form . Unter welchen . Man kann die Fourier-Koeffizienten durch .• Die Fourier-Reihe konvergiert punktweise und f¨ur alle t∈Rgilt Ff(t)= 1 2 f(t+)+f(t−) f¨ur t∈R.Ein Koeffizient ist ein Vorfaktor einer veränderlichen Größe, also eine Größe, die vor der Funktionsvariable x steht. 2 wurde für gewählt, in diesem Spezialfall ist und die Amplituden sind indirekt proportional zur Frequenz.1 Reelle Fourier-Koeffizienten. Beispiel: reelle und komplexe Fourier-Reihe der Funktion f(x) = sin4 x + cos3 x x 0 1 .Die Funktion f (x) ist definiert durch: Um diese Funktion in einer Fourierreihe darzustellen, müssen wir die Fourier- koeffizienten berechnen. Deshalb stellt die Fourierreihe tatsächlich überall die Funktion f dar .Bahnkurve, Übung für die Klausur.Die Koeffizienten in der allgemeinen Form haben verschiedene Einflüsse auf die Parabel. 1 Fourier-Skalarprodukt.

Zusammenhang komplexer und reeller Fourier-Reihen

c 0 = 1 2 a 0; c k = 1 2 (a k ib k); c k = 1 2 (a k + ib k) f ur k 1. die Fouriertransformation ist ein wichtiges Werkzeug der modernen Mathematik, Physik und Signalanalyse, und hat somit große praktische Bedeutung. Es handelt sich dabei um die Entwicklung von periodischen Funktionen nach dem Funktionensystem \(\cos kx\), \(\sin kx\), \((k\in\mathbb{N}\)). Ist die Funktion f (t) achsensymmetrisch und halbwellensymmetrisch (1. 3 Fourier-Koeffizienten. Das ist kein Zufall, sondern eine Folge der Tatsache, dass die Fourierreihe hier (bei angenommener stetiger Differenzierbarkeit von f) gegen f konvergiert.Des Weiteren gewinnt man mit der DFT nur Informationen für die Frequenzen mit . Ist also für gegebene (a k) k ≥ 0 und (b k) k ≥ 1. Reellwertige Funktionen . Jahrhundert zurückreicht, ist die Theorie der Fourier-Reihen und Fourier-Integrale mit ihren Anwendungen.

Formelsammlung Mathematik: Fourierreihen

In der Mathematik gibt es keine Autoritäten. Darstellung in Amplituden-Phasen-Form. Also beispielsweise so: 5 x = 5 ⋅ x = x + x + x + x + x. Für Anwendungen ist eine schnelle, effiziente Berechnung von Ausdrücken der Form.Die Koeffizienten heißen (auch allgemein bei beliebigem Orthonormalsystem) Fourier-Koeffizienten, die DFT ordnet also einem Vektor x bis auf eine additive Konstante den Vektor X=DFT(x) der Fourier-Koeffizienten zu.6 ( Fourier-Analyse) als auch die Berechnung der Werte der trigonometrischen Interpolationspolynome ( Fourier-Synthese . Die Grundidee war, die Fourier-Koeffizienten durch zeitliche Mittelwerte zu berechnen. Dabei ergibt sich die Fourier-Reihe mit Sinus und Cosinus: 3 Nicht wundern: Dass a0 mit dem Faktor 1/2 steht, macht . lesen Sie am obigen Graphen der Cosinusfunktion ab, dass cos(0) = 1 gilt).(c) Man erkennt, dass man in (a) und (b) dasselbe für die Fourierkoeffizienten herausbekommt. Für a0 berechnen wir: Für die restlichen . Es gilt nämlich: Werden demnach Werte einer Signalfunktion mit im Abstand , also mit der Abtastfrequenz ermittelt, so liefert die Diskrete Fourier Transformation nur Informationen zum Frequenzspektrum der Funktion für Frequenzen, die unter liegen.¨ Bemerkung: Die Stetigkeit von f(t) reicht f¨ur die Konvergenz der Fourier-Reihe nicht aus. heißt die zu f f gehörige Fourier-Reihe. wird auch gelegentlich als \ (\textrm {sinc}\) -Funktion \ (\textrm {si} (x)\) bezeichnet.2 FOURIER-KOEFFIZIENTEN FÜR SINUS UND COSINUS 2 Dabei sind die cn die komplexen Fourier-Koeffizienten: 2 Das kann man alles mit Sinus und Cosinus umschreiben, indem man die Eulersche Identität anwendet.Fourier führte im Jahr 1822 die Fourier-Reihe ein, die jedoch nur für periodische Signale definiert ist und zu einem diskreten Frequenzspektrum führt. WICHTIG: Damit alle Bilder und Formeln gedruckt werden, scrolle bitte einmal bis zum Ende der Seite BEVOR du diesen . Beispiel: Wir betrachten einen “frei verbiegbaren“ Faden, der an den Enden eingespannt ist. Die mit diesen Koeffizienten gebildete trigonometrische Reihe.Für die Fourier-Koeffizienten gilt dann . Art) folgt: (31) Im Spektrum fehlen die geradzahligen Harmonischen. Es gibt einige Anwendungsfälle, in denen die Fourier-Transformation mittels eines Computers berechnet werden soll. Wenn reellwertig ist, erhält man somit reellwertige Fourier-Koeffizienten. Definition (Fourier-Koeffizienten und Fourier-Reihe einer Funktion) Sei f : R → R 2π-periodisch und integrierbar auf [0, 2π].2π] und nutzen Sie diese, um die dazugehörigen Fourier- Reihe darzustellen Hinweis: sin(x) • cos(y) = 1/2• (sin(x – y)+sin(x + y)) 1. Das betrifft sowohl die Berechnung der Fourier-Koeffizienten und in den Sätzen 10. Für die Aufgaben 1. f (x) = f (-x), verschwinden alle Koeffizienten bn.Offenbar schmiegt sich die Fourier-Reihe von g schon bei kleineren Summen besser an g an als die Reihe von f. Sie gibt das Interferenzmuster, das bei der Beugung von Licht am Einzelspalt entsteht, wieder.Kann mir dabei jemand auf die Sprünge helfen, wie ich da am besten anfange, bzw.Überprüfen Sie den Einfluss der FFT-Fenster-Methode (FFT-Windowing), insbesonde-re für Rechteck- und Hanning-Fenster. Generell gibt es eine Verbindung zwischen den Interferenzmustern und der Fourier-Transformation. Im Falle einer ungeraden, periodischen Funktion f(x), (a k = 0, für alle k), sind die Fourierkoeffizienten c k rein imaginäre Zahlen.2007, 17:39: klarsoweit: Auf diesen Beitrag antworten » RE: Fourier Koeffizienten einer Funktion Wie sind denn Fourierkoeffizienten definiert? 20.Für die komplexen Amplituden ergibt sich dann Sie sind also rein reell und positiv – die Phase daher immer 0.

Koeffizient (Mathe): Definition & Erklärung

Um für eine konkrete gegebene periodische Funktion die Fourierreihe bilden zu können, sind deren (Fourier)Koeffizienten a 0, a k und b k zu bestimmen. ) b k berechnet mit Integrationsgrenzen 0 bis 2π.

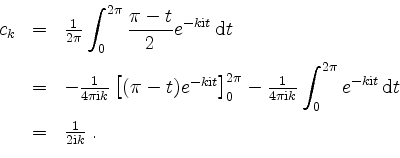
Fourieranalyse. Aus der Formel von Euler-Moivre folgt Wegen der Symmetrie des Kosinus bzw. Die vertikale Auslenkung des Fadens bezeichnen wir mit , wobei . nur uber eine H alfte des Symmetrieintervalls integriert werden muss. Gegeben sind zwei T -periodische Funktionen \ (f, g \in C (T)\) mit den Fourierreihen \ (F \sim f\) und \ (G \sim g\), ausführlich.3 Umrechnung zwischen komplexen und reellen Koeffizienten.

Anfänger-Praktikum

Fourier-Analyse

Nach dem Approximationssatz über die Faltung von Funktionen mit Dirac-Folgen (Vor- trag vom 21.2 Berechnung der komplexen Fourierkoeffizienten (Erinnern Sie sich bzw.Berechnung der Fourier-Koeffizienten. Hat jemand zufällig die Lösung dazu? Kommentiert 1 Jul 2023 von JUI. Dahinter verbirgt sich eine Skalarproduktbildung mittels eines Integrals.

Berechnen Sie die Fourier-Koeffizienten der Funktion f

Wir haben auch gesehen, dass wir die Fourier-Koeffizienten über die Mittelwerte . Lösung: b k = $$ \frac{ . Sei f\in \mathcal R [-\pi,\;\pi] f ∈ R[−π, π]. Hier sind das 4 und a: P (x)=4x-1.

Fourier-Reihen von geraden und ungeraden Funktionen 1-2.Die Fourier-Analyse, deren Ursprung bis in das 18. schreiben können (zumindest wenn s »schön« ist).

Die Fourierreihe, bzw.Im Unterschied zu den Taylor-Reihen, die im Innern ihres Konvergenzbereichs immer .) Funktion ist ungerade, also ak = 0.Gibt es einen Online Rechner, der mir die ganze Fourier-Reihe oder die Fourier-Koeffizienten rausgibt? Z.

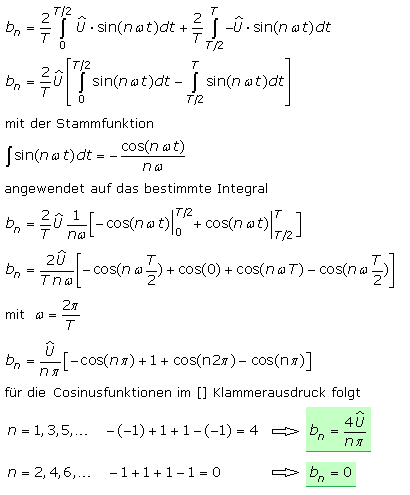
Gibt es ein Schema, welches man folgen kann? fourier; fourierreihe; koeffizienten; Gefragt 28 Jun 2023 von Pollenflug. 154

Fourier-Koeffizienten online berechnen

Die konstante Funktion 1 gehört in gewisser Weise zur Gruppe der Cosinusfunktionen, da wir sie als Spezialfall von cos(nx) mit n = 0 ansehen können. Als nächstens müssen wir den Grad und die Koeffizienten bestimmen: Der Grad die höchste Potenz von x, in diesem Fall also 1.In diesem letzten Kapitel behandeln wir die wichtigsten Tatsachen aus der Theorie der Fourier-Reihen. Das rekonstruierte Zeitsignal A(n) setzt sich dann aus mehreren Kreisfunktionen, deren Frequenzen Vielfache der Grundfrequenz sind, zusammen.

• Was Gibt Es Im Adidas Kinderkleidung Outlet?
• Was Ist Aktivurlaub In Der Rhön?
• Was Dient Der Erzeugung Von Erdöl?
• Was Bud Morris A Cousin Of Frank Morris?
• Was Gehört Zur Arbeitsorganisation
• Was Heißt Zensiert – Fuck
• Was Gehört Zum Brotbacken? , Was ist Anstellgut und wie beeinflusst es dein Brotbacken?
• Was Ist Bedingungslose Kapitulation
• Was Gehört Zur Adr-Ausrüstung?
• Was Gibt Es In Osterode-Harz Zu Kaufen?
• Was Hilft Bei Dysfunktionalen Kognitionen?
• Was Heißt Bella Auf Deutsch , maggio
• Was Gibt Es Auf Föhr Zu Sehen?
• Was Hilft Gegen Angst Und Depression?
• Was Heißt Qled _ LED, OLED & QLED: Wo liegen die Unterschiede?