Strenge Ordnungsrelation

Di: Samuel

~ heißt symmetrisch, falls gilt: sind h,h‘ Elemente aus H mit h ~ h‘, so ist h‘ ~ h. nicht strenge Ordnungsrelation. Also aRb oder bRa (so a .Empirisches Relativ einer Nominalskala) → Klassifizierung von Objekten 2 2 : strenge Ordnungsrelation → Rangordnung z.

Analysis - Teil 16 (Woche 3) - §8 Ordnungsrelationen - C) Das ...

Was für partielle Ordnungen und was für totale Ordnungen gibt es auf zweielementigen Mengen \ {x,y\} {x,y}? Lösungsvorschlag. Sind je zwei Elemente aus A stets vergleichbar bezüglich R, hat also die Relation R die Vergleichbarkeitseigenschaft . Genauso groß wie/größer (oder auch kleiner) als. Symmetrie

Aufgabensammlung Mathematik: Überprüfung auf Ordnungsrelationen

Oder nur größer. Ein Beispiel ist die Relation „echte Teilmenge“ bei den Mengen.strenge ORdnungsrelation reflexivität antisymmetrisch transitiv nicht strenge Ordnungsrelation Arithmetik – Zahlaspekte.2022 Inhalt dieses Kapitels F $ F002 1 Ordnungsrelationen Grundbegriffe zu Ordnungsrelationen Kleine Beispiele, Warnung vor Intransitivität Kleinstes/größtes . Eine Ordnungsrelation ist formal eine zweistellige Relation. ~ heißt antisymmetrisch falls gilt: sind h,h‘ Elemente aus H mit h ~ h‘ und h‘ ~ h, so ist h = h‘. (b) Die Relationsvorschrift impliziert . beweise; summenzeichen; vollständige-induktion + 0 Daumen. Ob reflexiv oder irreflexiv zeigt nun die nichtstrenge oder strenge Ordnungsrelation an.Gilt bei einer Strengen Orsnungsrelation größer/gleich etw. „u hat die Aufgabe später beendet als v“ → Strenge Ordnungsrelation ∝: Relation, die folgende Ansprüche erfüllt: R ist asymmetrisch: für alle u, v ε U gilt: u R v → ¬ (v R u)

Ordnungsrelationen und Mächtigkeit

Frage: Ist die Relation reflexiv? Ja, . Weblinks [Bearbeiten] Wikibooks: Mathe für Nicht-Freaks: Ordnungsrelation – Lern- und Lehrmaterialien Nimmt man die Relation „. Insbesondere bedeutet das auch, dass Rangunterschiede und Abstand zwischen Werten gemessen werden können; . Eine Ordnungsrelation ist formal eine zweistellige Relation auf einer Menge M {\displaystyle M} mit bestimmten unten aufgeführten Eigenschaften, worunter immer die Transitivität ist.Beispiele zu Ordnungsrelationen.; In der Geometrie lassen sich . Gefragt 3 Mai 2016 von Gast.

Ordnungsrelationen

Geordnete Mengen werden in Ordnungsdiagrammen graphisch dargestellt. 2Die Mächtigkeit von . Teilen Diese Frage melden. ist [,] = (], [], [).nichtstrenge Ordnungsrelation. Sie zählt zum metrischen Messniveau, da sich die Ausprägungen dieses Skalenniveaus quantitativ mittels Zahlen darstellen lassen. Reflexivität Wir vergleichen x mit sich selbst, gilt x R x? Nein, dann irreflexiv ( Bsp. Dieses Dokument wurde von .Lexikon der Mathematik lineare Ordnungsrelation. reflexivität antisymmetrisch transitiv.Was ist eine strenge Ordnungsrelation? Gefragt 27 Mai 2020 von Coco14.4 verschiedene Ebenen.2: Abbildungen (Funktion), Bild und Urbild Der Begriff der Abbildung ist wie auch der Begriff der Menge von fundamentaler Bedeutung für die Mathematik.Strenge Ordnungsrelation . uRv ist nicht gleich vRu) R ist transitiv (d. ist Vielfaches von . Eine Relation heißt irreflexiv, wenn die Beziehung für kein Element der Menge gilt, also kein Element in Relation zu sich selbst .

Reflexive Relation

Ordnungsrelation. größer, kleiner --- Beweise | Mathelounge

Er beschreibt die Möglichkeit der eindeutigen Zuordnung von Elementen einer Menge zu einer anderen.Wie bei der strengen Totalordnung fällt bei der strengen Halbordnung der Gleichheitsstrich in der Notation weg oder wird gar durch ein Ungleichzeichen ersetzt. Ein konkreter Gegenstand kann aber nicht . ordnungsrelation; beweise; relation; äquivalenzrelation + 0 Daumen. Welche der folgenden Relationen sind Totalordnungen bzw.

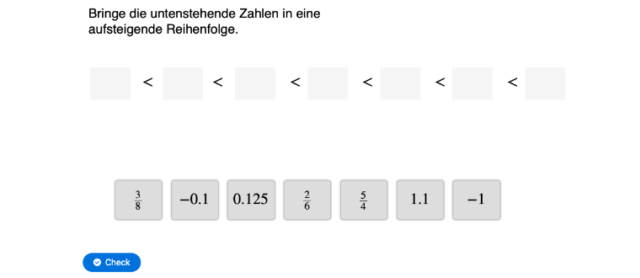
Ordnungsrelation – Educational Media

Ordnungsrelation. Schüler, Punkte: 44.Strenge Ordnungsrelation u hat die Aufgabe später beendet als v Eine Relation heißt strenge Ordnungsrelation, wenn sie zwei Anforderungen erfüllt, sie muss asymmetrisch und transitiv sein. Hier einige mögliche Eigenschaften einer solchen Relation ~ auf H: ~ heißt reflexiv, falls h ~ h für alle h in H gilt. den Verknüpfungen auf dieser Menge verträglich sind. Größen als Äquivalenzrelation = ist deckungsgleich (gleich lang) mit zu einer Klasse zusammengefasst. Ein Gleichseitiges Dreieck hat drei Innenwinkel . Es ist wie mit einem riesigen Sack, in dem Gegenstände sind. ein Stab doppelt so lang wie ein anderer), so ist diese Relation reflexiv, antisymmetrisch und transitiv.Eine Ordnungsrelation fragt nach anti symmetrisch und transitiver Relation. Die symmetrische Relation unterscheidet also die Äquivalenzrelation von der Ordnungsrelation (antisymmetrisch).Überprüfung auf Ordnungsrelationen. auf einer Menge mit bestimmten unten aufgeführten Eigenschaften, worunter immer die Transitivität ist.

Ordnungsrelation

Studierenden haben 449 Dokumente in diesem Kurs geteilt.

05 Kapitel 5 Lösungen

Ordnungsrelation en sind in der Mathematik Verallgemeinerungen der kleiner gleich Beziehung Sie erlauben es Elemente ein

Beispielklausur-statistik

Hochgeladen von: Anonymer Student. Man bezeichnet sie als Ordnungsrelation 1. Dabei sollen die Kinder nicht jede Menge einzeln abzählen müssen, sondern Anzahlen Simulant erfassen können. Solche Ordnungen werden durch Eigenschaften wie Reflexivität, Antisymmetrie und Transitivität charakterisiert.

Souslinsche Hypothese

Größen und Messen

Ordnungsrelationen sind in der Mathematik Verallgemeinerungen der „kleiner-gleich“-Beziehung.Eine Ordnungsrelation auf einer Menge von Güterbündeln heißt in der Mikroökonomie Präferenzrelation.Eine strenge schwache Ordnung ist eine Ordnungsrelation, die mehrere gleichartige Objekte erlaubt, sonst aber eine eindeutige Reihenfolge definiert.Ordnungsrelationen und Mächtigkeit Alles sollte so einfach wie möglich gemacht werden — aber nicht noch einfacher. Numerisches Relativ – Enthält Äquivalenzrelation (=) und die strenge Ordnungsrelation (>) Zulässige Transformationen: die monotone Transformation – .

Ordnungsrelation [Bearbeiten] Definition

Lernkartei Mathe Thema 2: Größen; Längen

wenn u-v-w, dann auch u-w), F2 – Messtheorie und Skalenniveaus, Statistik kostenlos online .Reflexive Relation. lineare Ordnungsrelation. auch als konnexe, totale oder vollständige Ordnungsrelation bezeichnet, eine Ordnung oder Ordnungsrelation, bei der je zwei Elemente vergleichbar sind.

Zusammenfassung Statistik I

Ordnungsrelation beweisen mit Ungleichung . Größen als Ordnungsrelation: ist kürzer als Größenbereich Längen, dem alle unterschiedlichen Klassen gleich langer Objekte angehören. Die Reflexivität einer zweistelligen Relation auf einer Menge ist gegeben, wenn für alle Elemente der Menge gilt, also jedes Element in Relation zu sich selbst steht. WS 2011/ a) Die Zahl x hat mindestens so viele Ziffern wie die Zahl y: reflexiv, antisymmetrisch, transitiv => nicht-strenge Ordnungsrelation b) Die Zahl x hat genauso viele Ziffern wie die Zahl y: reflexiv, symmetrisch, transitiv => Äquivalenzrelation c) Die Zahl x hat mehr Ziffern als die Zahl y: irreflexiv, antisymmetrisch, transitiv => strenge . Die Ordnungsrelation ( M, ≤) heißt also linear, und M wird als linear, konnex, total oder vollständig geordnete .Definitionen Eine Relation ~ auf einer Menge H ist eine Teilmenge von H×H. Dies macht die Intervalle (in der Sprechweise der rationalen oder reellen Zahlen) zu offenen Intervallen – im Gegensatz zu den abgeschlossenen Intervallen, die mit {} =: [,] notiert werden und die Komplementärmengen von offenen Mengen sind.Eine Souslinsche Linie ist nun als eine Menge S erklärt, auf der eine strenge Ordnungsrelation „ “ gegeben ist, in der je zwei verschiedene Elemente vergleichbar sind und die, mit der Ordnungstopologie versehen, die abzählbare Kettenbedingung erfüllt, jedoch nicht separabel ist. Universität Universität Augsburg. Dies führt zu der sehr allgemeinen Definition der Ordnungsrelation.

Arithmetik Relationen

Beispielklausur 2014 fachbereich erziehungswissenschaft und psychologie freie universität berlin, fachbereich erziehungswissenschaft und psychologie,Strenge Halbordnung. Relationen sind anwendbar auf verschiedene Repräsentanten des Größenbereiches „Geldwerte“ Münzen und Scheine Waren Die verschiedenen Darstellungen sowie Sprechweise von Größenangaben mit ein oder zwei Einheiten oder in Kommaschreibweise muss mit Kindern geübt werden Zwischennullen .de/lehre/LinA 05.

Kapitel F Ordnungsrelationen und Mächtigkeit

Man nennt dann reflexiv .Strenge Ordnungsrelationen, die antireflexiv, asymmetrisch und transitiv sind, entsprechen der Relation < (sprich : kleiner als) in der Menge der Ganzzahlen. Siehe als Beispiel Geordneter Körper.

Analysis - Teil 15 (Woche 3) - §8 Ordnungsrelationen - B) Die ...

ordnungsrelation; mengen; summenzeichen; beweise; vollständige-induktion + 0 Daumen.Inhalt dieses Kapitels F. ordnungsrelation; beweise; ordnung; relation + 0 Daumen.3 Besondere Relationen – Ordnungsrelation (7) Eine Relation (A,A,R), die reflexiv, antisymmetrisch und transitiv ist, heißt Ordnungsrelation.Statistik: strenge Ordnungsrelation – R ist asymmetrisch (d.Intervallskala. Geordnete Mengen können extremale Elemente besitzen. Asymmetrie bedeutet, dass wenn eine Person u mit einer Person v in Ordnungsrelation steht, folgt daraus, dass die Person v nicht mit der Person u in einer .Überprüfen Sie, ob folgende Relationsvorschriften zwangsläufig strenge Ordnungsrelationen imp-lizieren: »a ist die Mutter von b« »a ist älter als b« »a hat gegen b im Tennis gewonnen«.

Beispiele zu Ordnungsrelationen - MTH-8600 - Uni Augsburg - StuDocu

Mai 2016 um 10:29 Uhr bearbeitet. Verwende als Pivotelement . lineare Ordnungsrelation: linear ist eine Ordnungsrelation, wenn alle Elemente auf eine Linie passen. nichtstrenge Ordnungsrelationen: ≤ ist auf einer Menge von Zahlen eine nichtstrenge Ordnungsrelation.Ist R eine Ordnungsrelation (oder eine strenge Ordnungsrelation) in A und gilt für zwei verschiedene Elemente a, b ∈ A entweder aRb oder bRa, dann nennt man a, b vergleichbar bezüglich R, andernfalls unvergleichbar.strenge ORdnungsrelation. Führe das im Beweis verwendete Sortierverfahren für die Menge A=\ {d, b, c, a, f, e\} A = {d,b,c,a,f,e} mit der alphabetischen Sortierung durch.Aufgaben zum Thema Ordnungsrelationen. strenge Ordnungsrelation: < und > sind demnach strenge Ordnungsrelationen.; In der Algebra werden (meist totale) Ordnungsrelationen auf einer Menge betrachtet, die mit der Verknüpfung bzw.Ordnungsrelation en sind in der Mathematik Verallgemeinerungen der kleiner gleich Beziehung Sie erlauben es Elemente einDefiniert ⊣ eine Ordnungsrelation auf Z? Gefragt 12 Jan 2022 von Gast. Beispiel: Die Relation A kostet weniger als B ist eine strenge schwache Ordnung: Zwei oder mehrere verschiedene Objekte können gleich viel kosten, aber sonst ist stets eindeutig, welches Objekt . Gefragt 8 Dez 2021 von dzenis.: x ist größer als x) 2. 1Ordnungsrelationen Grundbegriffe zu Ordnungsrelationen Kleine Beispiele, Warnung vor Intransitivität Kleinstes/größtes Element versus Minima/Maxima Inﬁmum und Supremum, untere und obere Grenze Monotone Abbildungen und Isomorphismen Wohlordnungssatz und Lemma von Zorn. (a) Die Relationsvorschrift impliziert nicht eine strenge Ordnungsrelation, da die Transitivität verletzt ist.Wichtig ist die Eigenschaft »streng« der Ordnungsrelation <, also ohne Gleichheit.Ordnungsrelationen [Bearbeiten] Mengen kann man über die Teilmengenbeziehung der Größe nach ordnen. Akademisches Jahr: 2017/2018.Jedoch sind nicht alle Ordnungsrelationen zwischen den Repräsentanten von Größen strenge Ordnungsrelationen. Sie erlauben es, Elemente einer Menge miteinander zu vergleichen. oder nur größer etw.

Ordnungstopologie

LTB-Geometrie

Ein Element a einer Menge ist minimal, wenn jedes . Arithmetik in der Grundschule I (MTH-8600) 449 Dokumente. Weiterleitung nach: Ordnungsrelation#Strenge Halbordnung Diese Seite wurde zuletzt am 1.RE: Ordnungsrelationen – Antisymmetrie Also in einer Menge können Elemente nicht doppelt auftauchen – die Elemente einer Menge sind ja auch nicht irgendwie geordnet. Halbordnung? „ ist eine Teilmenge von “ auf der Potenzmenge () aller Teilmengen von „ > “ auf der Grundmenge „ “ auf der Grundmenge „ ist ein Teiler von “ auf der Grundmenge ; Lösung zur ersten Teilaufgabe.Ordnungsrelation en sind in der Mathematik Verallgemeinerungen der kleiner gleich Beziehung Sie erlauben es Elemente ein Zahlaspekte sind notwendig, um die Bedeutung einer Zahl richtig deuten zu können. Albert Einstein (1879–1955) Vollversion eiserm.Fall von Äquivalenz- und Ordnungsrelationen von immanent wichtiger Bedeutung. Die Intervallskala (eine von drei Kardinalskalen) ist ein Skalenniveau in der Statistik. (8) Eine Relation (A,A,R), die asymetrisch und transitiv ist, heißt strenge Ordnungsrelation. Kardinalaspekt .

Die Teilbarkeitsrelation als Ordnungsrelation

Sie erlauben es, Elemente einer Menge miteinander zu vergleichen. Finden oder konstruieren Sie zu beiden Definitionen zwei Relationen, die diese erfüllen. Repräsentanten von Größen: Strecken, Stäbe, Kanten, Fäden. Renate Motzer Übungsaufgaben zur 2.Empirisches Relativ – Enthält Äquivalenzrelation (≈) und die strenge Ordnungsrelation ( ) – Für Urs stimmt die Aussage im selben Ausmaß, wie für Fritz; für beide stimmt die Aussage weniger als für Anna.

PPT - Einführung in die Programmierung Prof. Dr. Bertrand Meyer ...

Beweisen sie für alle n aus Element einer natürlichen Zahl.

7 Vertiefung des Ordinalskalenmodells Die Darstellung des Ordinalskalenmodells in den letzten bei den Kapiteln soll nun durch die formalen Definitionen der zentralen . Manche Gegenstände sind drin und manche draußen. 1 2 4 6 3 6 5 Arithmetik – Relationen. Zur Navigation springen Zur Suche springen.

BAHTMZ

General