Runge Kutta Second Order – Runge-Kutta methods

Di: Samuel

Second order Taylor expansion in two variables Theorem: Suppose that f(t;y) and all its partial derivatives are continuous on D def = f(t;y)j a t b; c y d:g

List of Runge

org/learn/numerical-meth.third and fourth order Runge-Kutta methods 3 Applications the pendulum problem the 3-body problem in celestial mechanics MCS 471 Lecture 30 Numerical Analysis Jan Verschelde, 1 November 2021 Numerical Analysis (MCS 471) Runge-Kutta Methods L-30 1 November 2021 1 / 38. Its extended Butcher Tableau is: / / / / / / / / / / / / / / / / / / / / / / / / / / The first row of b coefficients gives the fifth-order accurate solution, and . 4e = 2m = r 4 e = 2 m = r. Chapter 2 Exercises; 3.

Predictor-Corrector and Runge Kutta Methods

I have two masses, and two springs which are atattched to a wall on one end. Consider the two-point boundary value problem.Runge-Kutta 4th order to solve 2nd order ODE using C++. Derivation of a fourth-order explicit Runge-Kutta method; 2.

Exponential Runge

PPT - Runge 2 nd Order Method PowerPoint Presentation, free download ...

Let’s discuss first the derivation of the second order RK method where the LTE is O ( h3 ). (42) Since we want to construct a second-order method, we start with the Taylor . Field values in OOF2) at time , and the first order differential equation (6. Adaptive Runge-Kutta Methods; 7.This scheme is not recommended for hyperbolic differential equation because this is more diffusive. This survey paper ranges over many aspects of .Video ansehen7:38The family of second-order Runge Kutta methods for solving ordinary differential equations. Runge-Kutta Methods 1 Local and Global Errors truncation of .

Runge-Kutta second order method | Numerical Analysis | SEM-6 | UNIT-4 ...

It is obtained from the Taylor series using similar approach we just discussed in the second-order method. Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Runge kutta 2nd Order • 3 likes • 1,301 views. 1 General purpose runge-kutta function for second order differential equations in Modern Fortran. Runge Kutta (RK4) 2nd order DE in C++ ERROR CODE.01 y 2 + sin ( 2 π t ) , This vector can be transposed to put . Python evaluating a second order ODE with RK4. 欧拉方法：欧拉方法是最基本的数值解法之一，属于一阶方法。. Website auswählen.

System of second order ODEs Runge Kutta 4th order

Nov 21, 2016 at 6:41 $\begingroup$ For the integration of heavenly bodies using several methods Moving stars around is always a good read.There is then the second-order Runge-Kutta method, third-order Runge-Kutta method, and so on. A new version of Nyström tree theory and the corresponding B-series theory are developed, based on which the order . The one you have described is (probably) the most popular and widely used one.The regions of absolute stability for the Euler method and the explicit Runge-Kutta methods of order 2, 3 and 4 are plotted in Fig. For this, we can define the formulas for Runge-Kutta methods as follows. Second-order Runge-Kutta methods; 7. 1 Python evaluating a .There are many Runge–Kutta methods. $\endgroup$ – Lutz Lehmann. I tried altering how the inputs to the equation are formatted but nothing has worked. RK methods: Runge-Kutta methods are actually a family of schemes derived in a specific . Ces méthodes reposent sur le principe de l’itération, c’est-à-dire qu’une première .0 are proposed. The interval of absolute stability for this method is $[-3,0]$ whereas for the second-order method we have $[-2,0]$. Runge Kutta 4th order Python.be/p5c6gSiQ-qcEuler’s method example 1:https://youtu.Les techniques de Runge-Kutta sont des schémas numériques à un pas qui permettent de résoudre les équations différentielles ordinaires.

How can I update this Runge-Kutta code for second order ODEs?

Manjushreearadhya2016 Follow.Runge kutta 2nd Order – Download as a PDF or view online for free.欧拉方法（Euler’s Method）和龙格-库塔方法（Runge-Kutta Methods）都是数值解常微分方程（ ODEs）的技术。. I need my Runge-Kutta to be able to accept it, but I am not sure how. In each exercise use the Runge-Kutta and the Runge-Kutta semilinear methods with the indicated step sizes to find approximate values of the solution of the given initial value problem at 11 equally spaced points (including the .Thus the Runge-Kutta needs four steps of calculation to get the next value yn + 1 y n + 1. Modern developments are mostly due to John Butcher in the 1960s. We’ll skip methods for which three evaluations of f are used and proceed to the Runge – Kutta method, the most widely used method, for which four evaluations of f are used to solve the initial .Autor: numericalmethodsguy This paper proposes and investigates a special class of explicit Runge-Kutta-Nyström (RKN) methods for problems in the form including third derivatives and denoted as STDRKN.1 Second-Order Runge-Kutta Methods As always we consider the general ﬁrst-order ODE system y0(t) = f(t,y(t)). For context I attached the system of equations. Here is the Runge-Kutta code.Runge – Kutta Method Calculator.Die -stufigen Runge-Kutta-Verfahren sind Einschrittverfahren, die durch Ausdrücke der folgenden Art gegeben sind: Dabei bezeichnet die Schrittweite zwischen den aufeinanderfolgenden Stützstellen und . After completing the iterative process, the solution is stored in a row vector called ysol. Runge kutta 2nd Order – Download as a PDF or view online for free. For more information on the method, go to https://nm.Learn via an example the second-order Runge Kutta method of solving ordinary differential equations. In the practical implementation, the product of a block Toeplitz matrix exponential and a vector is . Natural Language; Math Input; Extended Keyboard Examples Upload Random.Given a vector of unknowns (i. In other sections, we will discuss how the Euler and Runge-Kutta methods are used to . Since their first discovery by Runge (Math Ann 46:167–178, 1895), Heun (Z Math Phys 45:23–38, 1900) and Kutta (Z Math Phys 46:435–453, 1901), Runge–Kutta methods have been one of the most important procedures for the numerical solution of ordinary differential equation systems.

ordinary differential equations - Solve fourth order ODE using fourth ...

1 TVD Runge-Kutta To achieve higher order accuracy in the temporal discretization, one can use Total Variation Diminishing (TVD) Runge-Kutta (RK) methods.

Lecture 2

It is a second order ODE. In this presentation i have explained history of Runge kutta method and algorithm for .Before learning about the Runge-Kutta RK4 method, let’s have a look at the formulas of the first, second and third-order Runge-Kutta methods.Runge-Kutta 4th order method to solve second-order ODES. y ″ = f ( t, y), t ∈ [ t min, t max], y ( t min) = α, y ( t max) = β.In this paper we propose fast high-order numerical methods for solving a class of second-order semilinear parabolic equations in regular domains. For more videos and resources on .

4. Runge-Kutta methods — Solving Partial Differential Equations - MOOC

Since the ODE solvers we use can only be applied to a first-order ODE we need to rewrite the second-order ODE as a system of two first-order ODEs.

Runge Kutta Method

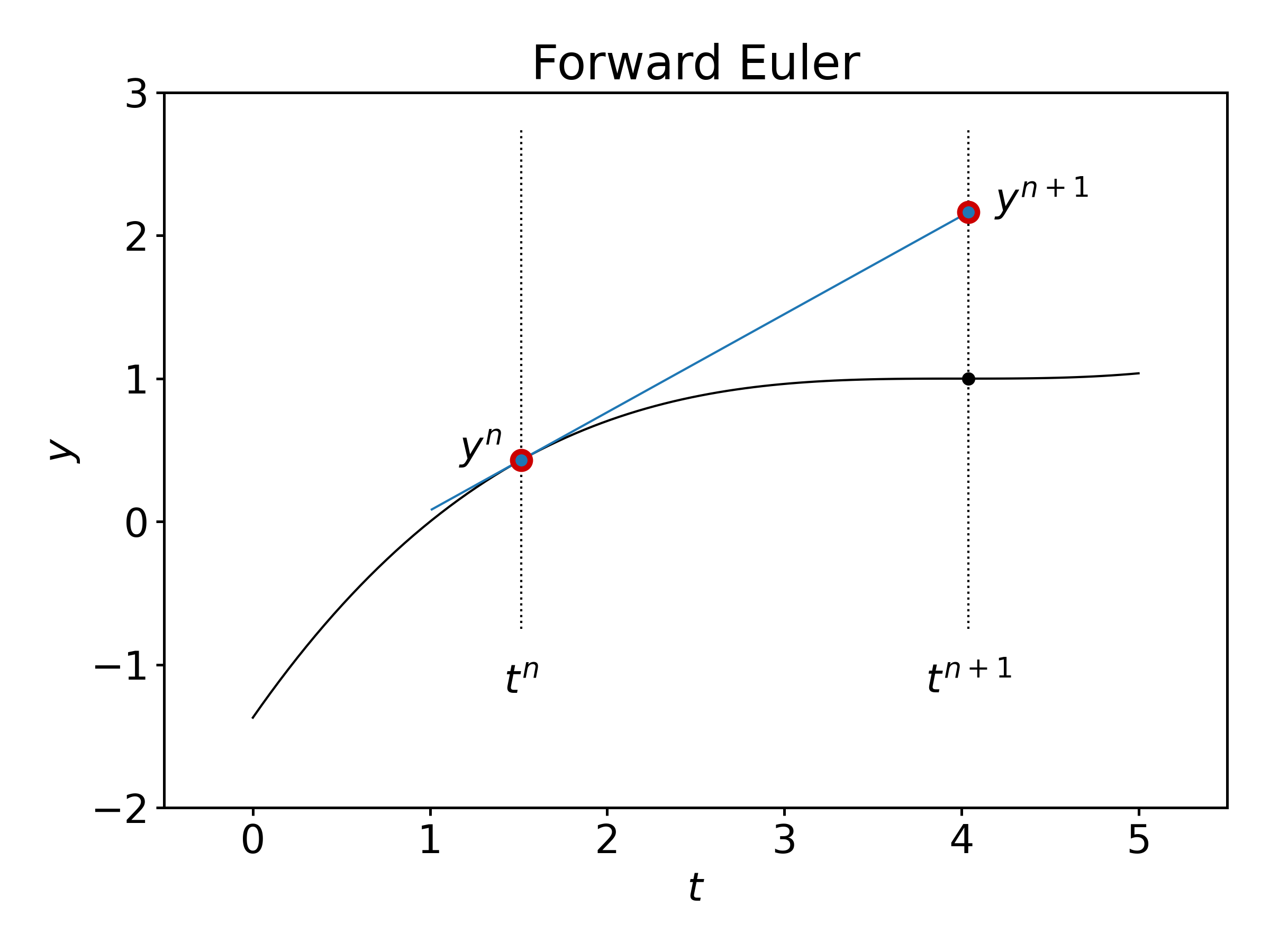
This research work has been carried out in order to compute direct solution of numerical method for order four of ordinary differential equations without reducing it to the system of first order differential equation through the application of both Euler and Runge-Kutta methods. A justified question is to ask wether the midpoint method yields better results than the Euler .$\begingroup$ I meant by Runge Kutta, been thinking of Newton’s method all day and must have typed it subconsciously $\endgroup$ – johnson. This method uses four points $k_1, k_2, k_3$, and $k_4$. A weighted average of these . We’ll solve the ODEs in the interval: 0 ≤ x ≤ 20 using 100 intervals. Solving initial value problems using explicit Runge-Kutta methods; 2.be/JhI6cLRjKHYRunge kutta 4th order method:https://youtu. Die Koeffizienten definieren das jeweilige Verfahren und können als Gewichte der Quadraturformel für das Integral interpretiert werden. For example, in the image below we see two estimates to the blue line.Classical Runge-Kutta-Nyström (RKN) methods for second-order ordinary differential equations are extended to two-derivative Runge-Kutta-Nyström (TDRKN) methods involving the third derivative of the solution.

2nd order Runge-Kutta (RK2)

Deriving order conditions using trees; 2.Runge kutta 2nd order method:https://youtu.This 2nd-order ODE can be converted into a system of two 1st-order ODEs by using the following variable substitution: u 1 1 and u 2 1 at x 0. Load 7 more related questions Show fewer related questions Sorted by: Reset to default Know someone who can answer? Share a link to this . I am not going to show you how to derive this particular method – instead I will derive the general formula for the explicit second-order Runge–Kutta methods and you can generalise the ideas. 6, and a time step h, and the solution yn at the n th time .

3 Runge-Kutta Methods

Each step in Euler’s method requires one evaluation of f and each step in the improved Euler method requires two evaluations of f. When comparing the three methods, one should therefore choose the stepsizes accordingly, that is in such a way that. The proposed methods are explicit in nature, and use exponential time differencing and Runge–Kutta approximations in combination with a linear splitting technique to achieve accurate and .An exponential Runge–Kutta method is employed to solve such a system of the ordinary differential equation. As the main innovation, the new explicit SRK methods have two advantages. Only first order ordinary differential equations can be solved by using the Runge-Kutta 2nd order method.Video ansehen10:58Learn the formulas of the Runge Kutta 2nd order method an ordinary differential equation of the form dy/dx=f(x,y), y(0)=y0.Runge-Kutta methods are a class of methods which judiciously uses the information on the ’slope‘ at more than one point to extrapolate the solution to the future time step. Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals. I’d like to speculate that there are 3 stages to understanding numerical ODE methods of the Runge-Kutta variety: low-order methods applied to the scalar case, transition to population models or mechanical second-order equations with 2 or 3 components,In this paper, new weak second-order stochastic Runge–Kutta (SRK) methods for Itô stochastic differential equations (SDEs) with an m-dimensional Wiener process are introduced. The methods involve one evaluation of second derivative and many evaluations of third derivative per step. Below is the python code for the 4th order Runge-Kutta that evaluates the following system of two 2nd order ODE: I need help fixing it. 1st Order Runge-Kutta . Elles font parties des méthodes les plus populaires de part leur facilité de mise en œuvre et leur précision. Adaptive step size control; 2.

Implementing a 2nd order Runge-Kutta method in Excel - YouTube

它的基本思想是利用微分方程提供的斜率信息来进行迭代。. 5 Runge-Kutta 4th order method to solve second-order ODES. The shooting method #. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, .While we won’t consider Runge-Kutta schemes of order higher than 4 in the course, we discussed the complexities one would face trying to construct equations for the coefficients $k_i$ for higher-order schemes.Autor: Jeffrey Chasnov

Runge-Kutta-Verfahren

Using 4th order Runge Kutta to solve the 2nd order differential equation of a damped oscillator.155) the second order Runge-Kutta estimate for is given by Implicit Runge-Kutta Methods. C’est Carle Runge et Martin Kutta qui, au début du XX e siècle, ont inventé ces méthodes. These methods sufficiently reduce computational efforts as well as provide the . For example, if your solution rep-resents a temperature proﬁle, spurious . Order of convergence of this scheme with grid refinement is very poor. Consider an ordinary differential equation of the form dy/dx = f(x, y) with initial condition y(x 0) = y 0. Nov 21, 2016 at 15:36. Theoretically, the proposed method is second-order accuracy in space and fourth-order accuracy in time, respectively.Join me on Coursera: https://www. The linear initial value problems in Exercises 3. We also gave insight into implicit Runge-Kutta schemes and provided an implementation of Qin and Zhang’s second-order implicit method.The shooting method — Runge-Kutta Methods.They were ﬁrst studied by Carle Runge and Martin Kutta around 1900.This question gets often asked. Elles ont été nommées ainsi en l’honneur des mathématiciens Carl Runge et Martin Wilhelm Kutta, lesquels élaborèrent la méthode en 1901. The Runge–Kutta–Fehlberg method has two methods of orders 5 and 4; it is sometimes dubbed RKF45 .

Runge-kutta second order method numerical analysis - YouTube

Two new explicit SRK methods with weak order 2. These methods guarantee that the total variation of the solution does not increase, so that no new extrema are generated.

Second order Runge Kutta method

0: 25 Aug 2019: Herunterladen. When I run my code it plots a flat line, but I know it should oscillate because I .

Second-order Runge Kutta methods

Given the IVP of Eq.Specific 2nd Order Runge Kutta for the Non-Linear Population Equation with an oscilation To write the specific 2nd Order Runge Kutta difference equation for the intial value problem we need f ( t , y ) = 0. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die .19 can’t be solved exactly in terms of known elementary functions.This is my function I am calling into my Runge-Kutta function. 对于一个给定的初值问题 .Join me on Coursera: https://imp. Extending Euler method to higher order method is easy and straight forward.Fourth-order Runge Kutta method¶ A classical method for integrating ODEs with a high order of accuracy is the Fourth Order Runge Kutta (RK4) method.The first row of b coefficients gives the third-order accurate solution, and the second row has order two.

Runge-Kutta methods

This means that this method is stable for larger values of $h$ so we can use fewer steps than the second . Determining the order of an implicit Runge-Kutta method; 3. [ ] Euler’s method does not take into account the curvature of the solution, whilst Runge-Kutta methods do, by calculating the gradient at intermediate points in the (time-)step.Second order Runge Kutta of Numerical differentiation with example. Higher-order Runge-Kutta methods; 7.How to derive the family of second-order Runge-Kutta methods for solving an ordinary differential equation.Les méthodes de Runge-Kutta sont des méthodes d’analyse numérique d’approximation de solutions d’équations différentielles.The Runge-Kutta 2nd order method is a numerical technique used to solve an ordinary differential equation of the form dy = f ( x , y ) , y ( 0 ) = y dx. System of differential equations; We begin with the simple Euler method, then discuss the more sophisticated RungeKutta methods, and conclude with the Runge-Kutta-Fehlberg method, as implemented in the MATLAB . Hot Network Questions When discharging a capacitor, why would a resistor make a difference if it is situated after .

BAHTMZ

General