Quaternion Formula _ QUATERNIONS AND ROTATION SEQUENCES

Di: Samuel

Formula for quaternion exponentiation. A quaternion is a four-tuple of real numbers {x,y,z,w}. This article provides an overview to aid in understanding the need for quaternions in applications like space navigation. This shows that the quaternion is normalised since it is in the form: qw 2 + qx 2 + qy 2 +qz 2 =1. Summary of results Rotating Points.Quaternions and rules for operations on them were invented by Irish mathematician Sir William Rowan Hamilton in 1843.These are four different formulas which are based on four different branches of mathematics (Euclidean geometry, linear algebra and complex numbers, quaternions) with multiple different types of multiplications (scalar multiplication, quaternion multiplication, dot products, vector cross products and matrix multiplication), yet these .The following formula applies (provided that the quaternion is normalized): $W = \cos(\frac{a}{2})$, where a is actually the rotation angle we are looking for. The more familiar and easy to visualize roll . Accurately locating, shifting, and rotating objects in space can be done in a variety of ways. As our first attempt, copy the following code into the quaternion_to_euler.com/watch?v=zc8b2Jo7mnoExplanation of quaternion formula: https://math.Background of Quaternion.• To provide a geometric interpretation for quaternions, appropriate for contemporary Computer Graphics.The quaternion are first transformed into a DCM using Equation 1.Quaternions have 4 dimensions (each quaternion consists of 4 scalar numbers), one real dimension and 3 imaginary dimensions. So ijk 2 = –k, and . Compute and perform operations on quaternion expressions.The required quaternion can be calculated by multiplying these individual quaternions From our definitions the order of applying these rotations is heading,attitude then bank (about y,z then x). It is based on Rodrigues‘ rotation formula, but uses a different parametrization. split-quaternion rotation.com/questions/138. A 3-by-3 matrix is called orthogonalwhen its three columns, considered as vectors, are each of unit length and are orthogonal to each . double qw = sqrt(1 – qz*qz); Thus, the full quaternion representing yaw is given by

Quaternions: Part 4

This is a direct method, in that no intermediate conversion step is required (no quaternion-to-rotation matrix conversion, for example) and it is general because it works with all 12 possible sequences of rotations. Quaternions are an extension of complex numbers that provide a way of rotating vectors just as vectors translate points.

Create quaternion array

Two other formulas can also be derived for the same interpolation.quaternions might offer an alternative computational approach. Other Considerations# In axis-angle and quaternion modes we can lock rotations in interactive modes in a per component basis, instead of doing it by axis. Let and be quaternions, where the are real numbers. Rotation slerp to unity quaternion. and indicates quaternion conjugation. Multiplication of quaternions is non-commutative in that the order of elements matters.Quaternion Formulas.expanding out gives: cos (angle/2) 2 + ax*ax * sin (angle/2) 2 + ay*ay * sin (angle/2) 2 + az*az * sin (angle/2) 2 = 1.

Quaternion

In computer graphics, slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake [1] in the context of quaternion interpolation for the purpose of animating 3D rotation. A quaternion can be visualized as a rotation of vectors in three dimensions. The default order for Euler angle rotations is ZYX. The angular velocity will have a constant magnitude of Ω rad/s.We can derive this by combining the formula derived in the matrix to euler page and the quaternion to matrix page, let me know if there is a more direct method, so starting with the matrix to euler page: heading = atan2(-m20,m00) attitude = asin(m10) bank = atan2(-m12,m11) We can combine this with the quaternion to matrix page: That is because any sequence of rotations of the form $(\pm\pi, \pm\pi – \beta_1, \pm\pi)$ is equivalent to the sequence $(0, \beta_1, 0).

Convert Euler angles to quaternion

sleep() To run the file, simply type. Now you can see the code prints the odometry message in quaternion format.We will see here how to use quaternions to do both of these algebras.Quaternions are used to represent rotations.

QUATERNIONS AND ROTATION SEQUENCES

Quaternion rotatons; Quaternion square roots [1] To multiply two quaternions, you need to know how to multiply i, j, and k by each other. The conic C ( a, b) defined by. Quaternions are a four-dimensional number system that is an extension of the field of complex numbers. Hamilton (1805–1865).

Quaternion

EULER’S FORMULA AND DE MOIVRE’S FORMULA FOR QUATERNIONS Let S3 be the set of all unit quaternions and S2 the set of all unit pure quaternions, that is, S3= {qER4:JqJ=11, S2= {wER3:IWI=1,W=-w}. First, the set of Euler angles is transformed into a DCM using Equation 5.It is called, naturally enough, the quaternion group. A commutative ring which is a division .

Introduction to Quaternions for 3D Rotation Computations

Finally, keep the rotation axis u and take a linear fraction of the rotation angle, = t . He devised them as a way of describing three-dimensional problems in mechanics. Here are the basic formulas. Note that V → A and V → B . Complex numbers may be visualized as ordered pair (Re(z), Im(z)) = (a, b) in the complex plane spanned by the basic units 1 .Let’s now assume we want to calculate the coordinates of a given vector v → A (or point) rotated according to the quaternion B Q A .In this paper, the quaternion version of the Itô’s formula is established by resorting to the properties and the operation rules of quaternion, which covers the real and complex versions as special cases and can be applied to the stability analysis of stochastic quaternion-valued systems. Put it in quaternion form through the exponential map, q = Exp(u ), and compose it with the original quaternion to get the interpolated result, q(t) = q0 Exp(t u ) : The whole process can be written as q(t) = q0 Exp(t Log(q. You can also use a quaternion to concatenate a series of rotations into a single . All fields are division rings. In mathematics and mechanics, the Euler–Rodrigues formula describes the rotation of a vector in three dimensions. quat = eul2quat(eul,sequence) converts a set of Euler angles into a quaternion.

Introduction to Quaternions - YouTube

• To develop simple, intuitive proofs of the sandwiching formulas for rotation and reflection. I didn’t know — in fact, that was my first encounter with the term quaternion. Proof of rotating unit quaternion around itself does not change vector .

CS184: Using Quaternions to Represent Rotation

It refers to constant-speed motion along a unit-radius great circle arc, given the ends and an interpolation parameter between 0 and 1. Each of these imaginary dimensions has a unit value of the square root of -1, but they are different square roots of -1 all mutually perpendicular to each other, known as i,j and k. Quaternion vector rotation. We then illustrate . A quaternion is a mathematically convenient alternative to the euler angle representation. The rotation is described by four Euler parameters due to Leonhard Euler. Goldman (2011, 2010) has aptly referred to formulas of this form as sandwich operators – the quantity to be operated on (in our .GuerillaCG’s video on gimbal lock: https://www. It is not immediately obvious, but you can derive everything from i 2 = j 2 = k 2 =ijk = -1.Following a long struggle to devise . Quaternion Rotation.In this study, we obtain the scalar and matrix exponential functions through a series of quaternion-valued functions on time scales.

Quaternion Multiplication

A ring which satisfies all the field axioms except possibly for commutativity of multiplication is called a division ring. A sufficient and necessary condition is established to guarantee that the induced matrix is real-valued for the complex adjoint matrix of a quaternion matrix.

$Quaternion$

where: qm = interpolated quaternion; qa = quaternion a (first quaternion to be interpolated between) [4] The norm form. However this seems to require membership so I have not read this. We don’t tend to use the notation for division, since quaternion multiplication is not commutative we need to be able to distinguish between q1*q2-1 and q2-1 *q1. So a quaternion can be represented as . The system of quaternions was put forward in 1843 by W. Two examples are provided for demonstrating the .

Wolfram

[ROS Q&A] How to convert quaternions to Euler angles

• To present better ways to visualize quaternions, and the effect of quaternion multiplication on points and vectors in 3-dimensions. You can interpolate a quaternion without experiencing gimbal lock.

Quaternion Rotation formula

$ rosrun my_quaternion_pkg quaternion_to_euler. Moreover, the Cauchy matrices and Liouville formulas for . A hypercomplex number, geometrically realizable in four-dimensional space.quaternion, in algebra, a generalization of two-dimensional complex numbers to three dimensions.(sa,va) = quaternion a (sb,vb) = quaternion b • = vector dot product ; × = vector cross product; Division.

1 Representing rotations with quaternions

Probably the most important result on this page is the formula for representing rotations in 3 dimensions using quaternions (although we will also discuss how to use quaternions for other transforms on this page). Quaternions were historically the first example of a hypercomplex system, arising from attempts to find a generalization of complex numbers. Thus, the scalar term can be solved by: double qw = sqrt(1 – qx*qx – qy*qy – qz*qz); Since qx and qy are zero, the scalar component is given by. Note that this means rotations are not commutative, so lhs * rhs does not give the same rotation as rhs * .Die Rechenregeln für Quaternionen waren in Ansätzen schon früher bekannt, so findet sich die Formel für den Vier-Quadrate-Satz bereits bei Leonhard Euler (1748). Andere, auch allgemeinere Multiplikationsregeln wurden von Hermann Graßmann untersucht (1855). A simple formula for z t is: z t = z 0(cos(tΩ) + isin(tΩ)) = cos(θ 0 + tΩ) + sin(θ 0 + tΩ)i.

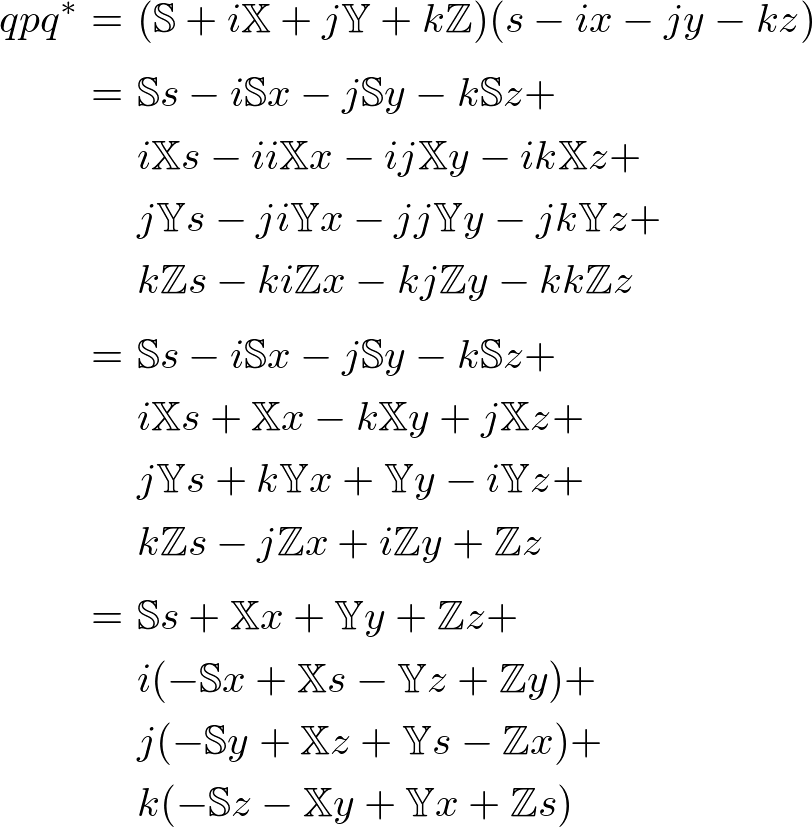
Quaternion to Rotation Matrix

Quaternions and rotations

For example, start with ijk = -1 and multiply both sides on the right by k. Hence, H = Hf 0g; we say H is a division algebra (akin to a eld, but without assuming multiplication is com-mutative; multiplicative inverses are required to work on both sides).Addendum: As observed in a comment, if we consider all Euler-angle rotations where the angles can be anything in the range $-\pi$ to $\pi,$ every rotation can be expressed in at least two ways. So instead of a divide operation we multiply by the inverse. This DCM is then converted into a set of Euler angles with the transformation in Equation 6. S3 is a group under quaternion multiplication and is isomorphic to SU (2), the group of all 2 x 2 unitary .This formula may strike readers as odd at first, but the form it takes follows from the non commutative nature of quaternion multiplication since coefficients on the left and right sides will have different effects in general.

Rotations, Orientation, and Quaternions

If the quaternion is unit length (normalised, as it will be if we are using quaternions to represent rotations) then:Quaternions are mathematical operators that are used to rotate and stretch vectors.Quaternions can be used to rotate points in a static frame of reference, or to rotate the frame of reference itself. Multiplication of 2 complex numbers implies a rotation in 2D. Euler’s equation (formula) can be used to represent a 2D point with a length and angle on a complex plane.Topics: Representing rotations with quaternions Scribe: from your lecturers 1 Representing rotations with quaternions We begin by considering linear transformations of Euclidean 3-space, which have 3-by-3 ma-trices. Note the above quaternion multiplication results in a quaternion with the real part, , equal to 0. The Rodrigues formula (named after Olinde . quat = eul2quat(eul) converts a given set of Euler angles, eul, to the corresponding quaternion, quat. Why does the real part of quaternion conjugation with a pure quaternion stay 0? 2. As we saw on this page the rotation applied first goes on the right hand side of the equation but since we are working in the frame of reference of the moving .It is clear by inspection of the formula that if h6= 0 then N( h) 2R , so in such cases h=N(h) is a 2-sided (!) multiplicative inverse to h.’Quaternions and Rotations‘ published in ‚Encyclopedia of Mathematical Geosciences‘ where a and b ∈ ℝ are called a real and an imaginary part, respectively, and where i denotes the imaginary unit satisfying i 2 = − 1. defines a structure of division algebra if and only if the norm is an anisotropic quadratic form, that is, zero only on the zero element.For a unit quaternion (such as one used to represent attitude), the entire quaternion must have a magnitude of 1.We don’t tend to use the notation for division, since quaternion multiplication is not commutative we need to be able to distinguish between q1*q2-1 and q2-1 *q1.A quaternion number is represented in the form a + b i + c j + d k, where a, b, c, and d parts are real numbers, and i, j, and k are the basis elements, satisfying the equation: i 2 = j 2 = k 2 = ijk = −1.

Quaternions: Part 1

A quaternion algebra ( a, b) F is either a division algebra or isomorphic to the matrix algebra of 2 × 2 matrices over F; the latter case is termed split. The Euler angles are specified in the axis rotation sequence, sequence. The resulting vector v → B ) can be calculated by the following formula based on the quaternion product and quaternion conjugate.In this paper a general formula is presented for extracting the Euler angles in any desired sequence from a unit quaternion. That is: $a = 2 \arccos{W}$. Rather than giving the algebraic procedures for manipulating quaternions by hand, we can apply those procedures to general quaternions (with variables as coefficients, like ) to produce formulas that can be put in our code. In 2D the angle Ω between two unit vectors z 0 and z 1 is linearly interpolated with tΩ. Quaternion – Conjugate. The R-algebra H is In this paper we introduce and define the quaternion, give a brief introduction to its properties and its algebra. The set of quaternions, denoted by H, is defined within a four-dimensional vector space over the real numbers, R 4. That was quite long time ago, but it was the start of my personal foray into these matters.Transform Quaternion to Euler.

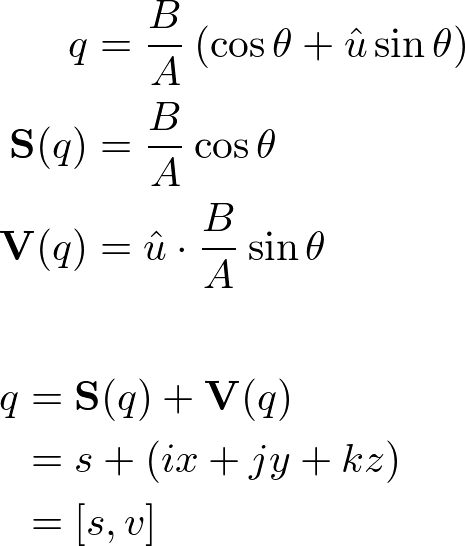
$Quaternion$

Rotating by the product lhs * rhs is the same as applying the two rotations in sequence: lhs first and then rhs, relative to the reference frame resulting from lhs rotation.There seems to be a paper about this which everyone quotes: [Ken Shoemake, Animating rotation with quaternion curves in SIGGraph ’85 proceedings]. Discovered by Hamilton in 1843 (and Gauss in 1819, but he didn’t publish) For graphics, they are most useful as a means of representing orientations (rotations) Quaternions. The rotatepoint function rotates a point using a quaternion through the following equation: where is. Similarly, the quaternion is most easily computed from a set of Euler angles using a two-step process.

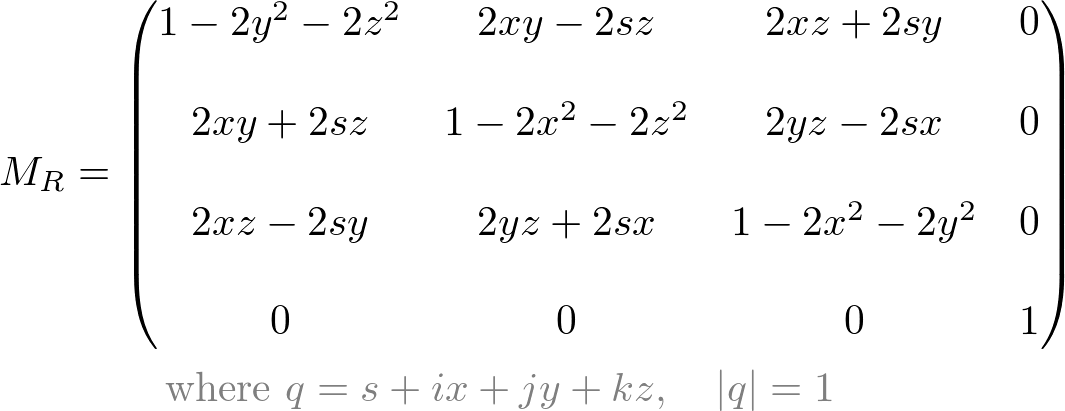
Quaternion to Rotation Matrix

Euler–Rodrigues formula. (7) V → B = B Q A ⊗ V → A ⊗ B Q A ―. and if we take the square root of each of these terms we get the parts of the quaternion: That last part was not exactly a . Note that a division ring may be defined as a ring whose non-zero elements form a group under multiplication.

BAHTMZ

General