Punktweise Konvergenz Funktionenreihe
Di: Samuel
KARLSRUHER INSTITUT FUR TECHNOLOGIE INSTITUT FUR ANALYSIS
Aufgabe 144: Integralkriterium für Reihen. FB Mathematik und Informatik, Universität .Diese nähern sich von oben immer mehr der Null an und man kann intuitiv sagen: Die Folge geht beliebig nah an . Im Fall der Konvergenz entspricht = auch dem Grenzwert der Partialsummenfolge. In jedem abgeschlossenen Intervall ohne Unstetigkeitsstellen von f ist die Konvergenz gleichmaßig. Aufgabe 471: Punktweise und gleichmäßige Konvergenz von Funktionenfolgen. Aufgabe 472: Konvergenz von Funktionenreihen. Potenzreihen Beispiele: Randpunkt 1. Moin, ich bräuchte dringend Hilfe, wie ich die punktweise Konvergenz der Folge Untersuche. Die Umkehrung gilt nicht: Um ein Gegenbeispiel zu nden, brauchen wir angesichts des Satzes 1. Wir haben geklärt, dass eine Reihe = der Folge = = der Partialsummen entspricht. linksseitige Limes. Ansonsten divergiert die Reihe. Das würde ja bedeuten, dass ich jedem einen Reihenwert zuordnen kann, gegen den die Reihe für ein jeweiliges strebt. The Art of Convergence Tests.; Die Folge = strebt gegen . Deshalb wurde bei x n für x=2 eingesetzt (wegen Supremum) und bei 1/x n wurde für .2012, 08:39: Nisi23: Auf diesen Beitrag antworten » Naja das weiß ich.Die Funktionenreihe konvergiert folglich auf ( 1;1] punktweise gegen die unstetige Funktion f: ( 1;1] !R; x7! (1; falls x2( 1;1); 0; falls x= 1: Da jedoch die Partialsummen der Funktionenreihe stetige Funktionen (ja sogar Polynome) sind, kann die Konvergenz nicht gleichm aˇig sein, da sonst f ja dann ebenfalls stetig sein m usste.Wir betrachten für jedes n∈ℕ die durch f n x =x n gegebene Funktion f n:I ℝ .ige Konvergenz Sei X eine nichtleere Menge, (N;d) ein metrischer Raum und (fn)n2Neine Folgevon Funktionen fn: X ! N. Zu einer Funktionsfolge (f_n) (f n) kann man eine unendliche Reihe der Form \sum\limits_ {k=1}^\infty f_k k=1∑∞ f k bilden, diese heißt Funktionsreihe. Daher ist sie punktweise konvergent gegen die Grenzfunktion f (x)=0 f (x)= 0. Interaktive Aufgabe: Interaktive Aufgabe 148: Konvergenz von Folgen, Reihen und Funktionenfolgen, Multiple Choice.
Kompakte Konvergenz
(Oder Summenfunktion) Die Grenzfunktion s — limn -+00 sn heißt Summe der Reihe Schreibe E Jfk Oder S ( x e D. Man sagt, daß eine Folge von Funktionen fn P L1 im Mittel gegen eine Funktion f P L1 konvergiert, falls }fn ́ f}1 Ñ 0. Hier wollen wir überlegen, welche Aussagen man über das Konvergenzverhalten von Funktionenfolgen bzw. Gleichm aˇige Konvergenz ) Punktweise Konvergenz Aber: f n (x) 0 1/n 1 Gleichm aˇige Konvergenz1 .Added Apr 13, 2013 by Math_Man in Mathematics.2012, 11:05: Hansen38: Auf diesen Beitrag antworten » Also ich verstehe nicht. Aber natürlich kann der Limes einer Folge stetiger Funktionen auch stetig sein, wenn die Konvergenz nicht gleichmäßig, sondern nur punktweise ist, siehe Beispiel 21. Der Schritt zu Funktionenreihen ist dann auch nicht mehr weit. Aus fn(x) =⇒ f(x) folgt fn(x) → f(x). Punktweise konvergente Folgen haben einige schlechte Eigenschaften: Die Folge der im Intervall [0, 1] durch f n (x) := x n definierten stetigen Funktionen . punktweise/gleichmäßige Konvergenz. Du kannst einfach weglassen.Gegeben ist die Funktionenreihe ∑ n²/√n! (x n +1/x n ) x∈ [1/2 ;2].me/Rafau85?country.Definition: (Punktweise und gleichmäßige Konvergenz) Die Funktionenreihe E k _ 0 heißt punktweise bzw.
Intro Funktionenreihen
8 Gleichm¨aßi ge Konvergenz impliziert punktweise Konvergenz. Aufgabe 466: Konvergenz von drei Reihen (2 Varianten) Aufgabe 467: Konvergenz von zwei Reihen.Studimup Mathe. Aufgabe 189: Konvergenzradius von Potenzreihen. Saving to notebook! Anmelden. Voraussetzung für die gleichmäßige Konvergenz ist punktweise Konvergenz.
Konvergenz: Folgen und Reihen von Funktionen
In der Mathematik nennt man eine Folge oder Reihe von Funktionen auf einem topologischen Raum mit Werten in einem normierten Raum kompakt konvergent, wenn sie auf jeder kompakten Teilmenge von gleichmäßig konvergiert . Infinite series can be very useful for computation and problem solving but it is often one of the most difficult. Es ergibt sich die harmonische Reihe. Dankeschön! Kommentiert 4 Jan 2018 von Aaaaa5. Normalerweise teilt sich diese Arbeit in zwei Arbeitsschritte auf: Zunächst versucht man auf einem Schmierblatt, eine Beweisidee zu finden, die man danach im zweiten Schritt in einem Beweis umsetzt und ins Reine schreibt.1 ist die Summe der Reihe im Intervall \([\delta,2\pi-\delta]\) stetig. series-convergence-calculator. Dafür müssen alle Werte aufsummiert werden und nachgeprüft werden, ob die Reihenwerte konvegieren oder nicht. Wie es prinzipiell funktioniert weiß ich, bin mir bloß explizit bei der Aufgabe unsicher.
Mathematik-Online-Aufgabensammlung: Konvergenz: Reihe
Insbesondere sind wir an Stetigkeitseigenschaften der Grenzfunktionen interessiert.2 Die Funktionenfolge (fn)n2Nkonvergiert auf X gleichm˜a.1) fn!f (n!1) :() 8z2D: lim n!1 fn(z) = f(z) 8z2D: 8>0 : 9N= N(z;) 2N : 8n N : jfn(z) f(z)j0 : 9N= N() 2N : 8n N;z2D : jfn(z) f(z)j< : 166.Die Funktionenfolge konvergiert also für alle Punkte x x aus ihrem Definitionsbereich. nicht recht sicher, wie ich .1 einfach eine Folge stetiger Funktionen zu nden, welche punktweise gegen eine nichtstetige Funktion konvergiert.Falls (f k) eine konvergente Funktionenfolge ist, so existiert zu jedem x ∈ ∈ D der eindeutig bestimmte Grenzwert von (f k (x)) und deswegen auch g, . Hallo zusammen, das neue Semester läuft, also wird es gelegentlich wieder Fragen von mir geben :-D) Bei dieser Aufgabe bin ich mir z. zu b) (ii): Wegen . Nach dem Majorantenkriterium von Weierstraß muss ja nun das Supremum aus (x n +1/x n ) bestimmt werden und die dann entstandene Zahlenreihe auf Konvergenz untersuchen.7) lediglich die Konvergenz im quadratischen Mittel zeigt, woraus nicht auf die punktweise Konvergenz geschlossen werden kann. Tut sie das für alle \(x\) aus einem betrachteten Bereich, so sagt man, dass die Funktionenfolge auf diesem Bereich punktweise (daher der Name) gegen eine Grenzfunktion konvergiert. gleichmäßig konvergent, wenn die Folge (sn) der Partialsummen punktweise bzw. Send feedback | Visit Wolfram|Alpha. Die Funktionenreihe ∞ ∑ k = 0 f k heißt konvergent, wenn die Summenfolge (n ∑ k = 0 f k) n=0.
Punktweise/ gleichmäßige Konvergenz
Get the free Folgen und Reihen widget for your website, blog, Wordpress, Blogger, or iGoogle.Funktionenfolgen – punktweise Konvergenz Dauer: 02:57 Funktionenfolgen – gleichmäßige Konvergenz Dauer: 04:49 Funktionenreihen Dauer: 04:18 Harmonische Reihe Dauer: 03:36 Geometrische Reihe Dauer: 02:37 Potenzreihen Dauer: 05:16 Wurzelkriterium Dauer: 02:59 Taylorreihen. Hier kann deine Reihe als eine Funktion eingegeben und den Anfangswert der Reihe bestimmt werden.Konvergenzbereich.29: (Konvergenz von FOURIER-Reihen) Ist f : R !R eine T-periodische, stuckweise glatte Funktion (s.
Punktweise Konvergenz einer Funktionenreihe
Bekanntlich gilt für jedes x∈I lim n ∞ f n x =0 . Eine Reihe konvergiert, wenn die Folge der Partialsummen konvergiert. Setze in die Potenzreihe ein und fasse es mit dem anderen Faktor zusammen. Ähnliche Fragen. Alle Konvergenzaussagen übertragen sich von den Funktionsfolgen auf die Folge der Partialsummen s_n=\sum\limits_ {k=1}^n f_k sn = k=1∑n f k. Ähnliche Beiträge im Blog von Symbolab. Diese haben wir oben gezeigt und die Grenzfunktion f (x)=0 f (x)= 0 ermittelt.Funktionenreihe: punktweise aber nicht gleichmäßig konvergent.Punktweise Konvergenz bedeutet: Wir nehmen jeweils ein festes \(x\) und schauen, ob die Folge der Funktionswerte gegen einen Grenzfunktionswert konvergiert.Gleichmaßige und punktweise Konvergenz¨ Buch Kap. absolut gleichmäßige Konvergenz. Zun achst ist klar, dass Satz (7.Entscheidungsbaum zur Konvergenz und Divergenz von Reihen. 2) Gleichmäßige Konvergenz.überprüfe unbestimmte Reihen auf Konvergenz Schritt für Schritt.Kompakte Konvergenz.

gleichmäßig konvergiert.

(Konvergenz der allgemeinen harmonischen Reihe) Um die Konvergenz mit Hilfe des vorherigen Satzes zu zeigen, müssen wir, da alle Summanden nichtnegativ sind, für die Partialsummenfolge () = (=) eine obere Schranke finden.23, bedeutet auch die gleichm¨aßige Konvergenz von Funktionenfolgen, dass man in der Konvergenzdefinition etwas unabh¨angi g von einem Parameter w¨ahl en kann, n¨amlic h n0 unabh¨angi g von x.Potenzreihen Beispiele: Randpunkt -1. Danach geht es weiter mit einem Video zu Potenzreihen.Sei D ein Intervall reeller Zahlen und (f k) eine Folge von auf D definierten reellwertigen Funktionen.Konvergenz im quadratischen Mittel Zun achst wenden wir uns der punktweisen Konvergenz der Fourierreihe S(x) = X1 n=1 f^(n)einx zu.
Punktweise/Gleichmäßige Konvergenz von Funktionenreihen
Authors and Affiliations.Bei gleichmäßiger Konvergenz hängt der Index N nur von ϵ, nicht aber – wie bei punktweiser Konvergenz an jeder Stelle von \({\mathfrak{D}}\) – noch von der Stelle \(x\in {\mathfrak{D}}\) ab.21), so konvergiert ihre FOURIER-Reihe punktweise gegen f. Aufgabe 129: Konvergenzradius der Binomische Reihe. Tats achlich hat Paul du Bois-Reymond (1831{1889) eine stetige Funktion f2C 2ˇ Aber man sollte das getrennt zeigen. Wir betrachten die ersten Der Reihenrechner . 76 Die Limesfunktion f ist nat ̈urlich nur eindeutig bis auf Modifikation auf einer Nullmenge.Untersuchen Sie die folgenden Funktionenreihen auf punktweise Konvergenz und gleichmäßige Konvergenz: a) (Autor: Joachim Wipper) automatisch erstellt am 2.; Alle diese Erklärungen beschreiben intuitiv, was wir in der Analysis den Grenzwert einer Folge nennen. Mein Ansatz zur punktweisen Konvergenz ist folgender: Im Skript steht: „Die Funktionenreihe konvergiert punktweise, wenn für jedes die Funktionenreihe fn (x) konvergiert.
Potenzreihen Konvergenz und Potenzreihen Beispiele
gleichmäßige Konvergenz
Mit Taylorreihen kannst du glatte Funktionen .
Mathematik
ig ge- gen die Funktion f: X ! N; wenn f˜ur jedes > 0 ein n0 2 Nexistiert, so dass d ‡ fn(x);f(x) < f˜ur alle n ‚ n0 und alle x 2 X: Beachten Sie: .x=de_DEIn diesem Video untersuchen wir Fu.Konvergenz von Fourier-Reihen Buch Kap.aus gleichmäßiger Konvergenz folgt punktweise Konvergenz: 18.n 1 punktweise gegen die Funktion f, mit f(x) = 8 0 0; x= 0 ˇ 2; x08n 0 2N9n n 0;x 0 2R .; Je größer ist, desto mehr nähert sich = der an. Hierbei bildet der folgende Satz die Grundlage. Deshalb weiß ich nicht wie man nur punktweise Konvergenz zeigen kann. Widget zur Veranschaulichung von Folgen und Reihen und ihrer Konvergenz oder Divergenz. Es soll betont werden, dass die Bedingung () keine Beziehung zwischen unterschiedlichen Punkten x und y in D herstellt; . Definition 1: Sei M ⊂ ℝ ℕ, und für n ∈ ℕ seien Funktionen f .Aufgabe 126: Konvergenz von Folgen und Reihen.Definition (Konvergenz im Mittel).verwendet in: Reihe/ Gleichmäßige Konvergenz.
gleichm aˇigen Konvergenz der Fourier-Reihe.Supremumsnorm beschränkter Funktionen, punktweise und gleichmäßige Konvergenz, Stetigkeit und Differenzierbarkeit der Grenzfunktion, Konvergenz von Funktionenreihen, Potenzreihen. Jetzt musst du noch einsetzen.Punktweise Konvergenz (6.Aufgaben: Aufgabe 346: Gleichmäßige Konvergenz von Funktionenfolgen.
Punktweise und gleichmäßige Konvergenz Aufgaben 3 und 4
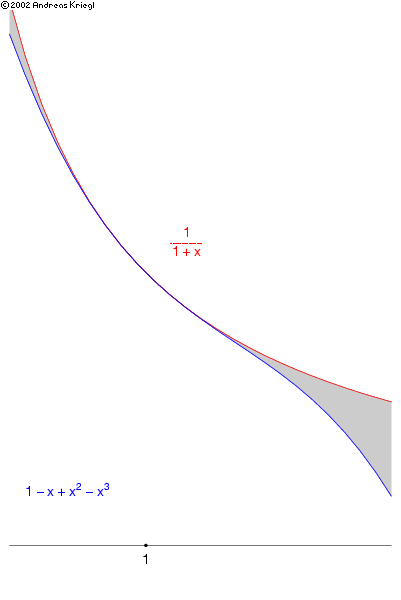
Funktionsreihen. Seine Bedeutung erhält der Begriff der kompakten Konvergenz aus der Tatsache, dass aus .Wir verwenden auch die Notation \(\lim _{n\rightarrow \infty } f_n\) für den Grenzwert, müssen dabei aber klarstellen, dass der punktweise Grenzwert gemeint ist. normale Konvergenz.Heute werden wir uns ein paar Funktionenfolgen anschauen und diese auf punktweise und gleichmäßige Konvergenz überprüfen.Daraus folgt die behauptete gleichmäßige Konvergenz. Falls ∞ ∑ k = 0 f k eine konvergente Funktionenreihe ist, so existiert die eindeutig .Wir schreiben bisweilen „ \(f_n\rightarrow f\) punktweise“. In diesem Fall ist der .
Folgen und Reihen
Funktionenreihe
Author information. Gemäß Satz 21. Im Anschluss erklären wir dir alles rund um Taylorreihen. Gefragt 28 Feb von Benni444444.; Die Folge = erreicht im Unendlichen die . Aufgabe 151: Integralkriterium für Reihen.In diesem Kapitel wird erläutert, wie man die Konvergenz und Divergenz einer Folge beweisen kann. Der Satz von der Majorisierten Konvergenz besagt also, daß eine punktweise konvergierende .Konvergenz der Reihen. Die¨ Umkehrung gilt im Allgemeinen nicht.Ein Beispiel für nicht-gleichmäßige Konvergenz Sei I:=]0,1[ . Gegeben sei eine Funktionenfolge , .Falls du meine Arbeit durch eine kleine Spende unterstützen möchtest: https://paypal.Es ist klar, dass gleichm aˇige Konvergenz auch punktweise Konvergenz impliziert. Folgen und Reihen von Funktionen. ∞ punktweise konvergiert.War schon die ganzen Tage am grübeln, warum ich denn nichts konkretes für die punktweise Konvergenz finde und sich alles so aehnelt.Gliederung Funktionenreihen.

Gib eine Aufgabe ein. Dabei verwenden wir einen ähnlichen Trick wie bei der Divergenz der harmonischen Reihe.Nun zur Untersuchung der punktweisen bzw. Es sei f(x ) der rechtsseitige, bzw. 3 Bemerkung Aus gleichmaßiger Konvergenz folgt punktweise Konvergenz.
Ein Beispiel für nicht-gleichmäßige Konvergenz
Untersuchen Sie die folgenden Funktionenfolgen auf punktweise und gleichmäßigeKonvergenz: (a) fn: (-inf,-1] –> R , fn (x) = n*x*e^ (-nx)^2.Punktweise Konvergenz einer Funktionenreihe Universität / Fachhochschule Funktionenreihen Tags: Funktionenreihen . Download to read the full chapter text. Hey, folgende Reihe soll punktweise, aber nicht gleichmäßig konvergieren auf diesem Intervall: Ich konnte herausfinden, dass die Reihe punktweise konvergiert, weil: Leider weiß ich nun nicht weiter, wie ich gleichmäßige Konvergenz widerlegen sollte?! Bitte um Hilfe! 10.Eine Funktionenfolge konvergiert punktweise gegen eine Funktion , wenn für alle Stellen aus dem gemeinsamen Definitionsbereich die Folge gegen konvergiert.8 : Sei f stuckweise stetig di erenzierbar, dann konvergiert die Fourierreihe punktweise, und es . Find more Mathematics widgets in Wolfram|Alpha. Reihen von Funktionen treffen kann. entspricht der Summe einer Folge an verschiedenen Werten eines Intervalls. Gegenbeispiel Die Folge konvergiertpunktweisegegen dieunstetigeGrenzfunktion f(x) = ˆ 1 fur¨ x = 0; 0 fur 0¨ Die punktweise Konvergenz ist in der Analysis ein Konvergenzbegriff für Funktionenfolgen. (f k) heißt punktweise konvergent auf D, wenn für jedes x ∈ ∈ D die Zahlenfolge (f k (x)) konvergiert. Geben Sie je ein Beispiel für eine punktweise konvergente .Punktweise Konvergenz. Sei D ein Intervall reeller Zahlen und (f k) eine Folge von auf D definierten reellwertigen Funktionen. Ein anderes Problem? Stell deine Frage. Zunächst zeigen wir dir Funktionenfolgen und gehen erst auf punktweise und dann auf gleichmäßige Konvergenz ein.Bei verschiedenen Lehrbuchautoren werden im Zusammenhang mit der Konvergenz von Funktionenreihen \(\sum f_{k}\) folgende Konvergenzbegriffe verwendet: punktweise Konvergenz. Die ist bekanntlich divergent. Betrachte dazu die Funktionen f n: [0;1] !R, welche . Satz 5412D (Kriterium von .Nimmt man also als f:I ℝ die Null-Funktion, so hat man ∀x∈I: f n x f x , mit anderen Worten: die Funktionenfolge f n konvergiert im Intervall I punktweise gegen die Funktion f , alsoFunktionenfolgen, Funktionenreihen, Potenzreihen
Funktionenreihe: punktweise aber nicht gleichmäßig konvergent