Permutationen In Mathematik , Zyklen von Permutationen
Di: Samuel
Die Berechnung erfolgt mittels Multinomialkoeffizienten.Permutationen werden auch in der so genannten Zyklenschreibweise angegeben. Wegen Satz 5325E können wir jede Permutation als Produkt von Transpositionen darstellen.Permutation mit Wiederholung.Zykel\ ergeben. There are basically two . Innerhalb der abzählenden Kombinatorik gibt es Permutationen, Variationen und Kombinationen. Schritt 1: Definieren Sie Ihre Elemente – Listen Sie zunächst alle Elemente auf, für die Sie Permutationen generieren möchten.Autor: musstewissen Mathe
Permutationen
Permutationen sind Vertauschungen von Objekten. In fact every outcome will appear on the list 6 times, since every outcome can appear in \(3! \) orders. Unsere frühere Definition: Eine Permutation ist . Permutationen Eine Permutation von Objekten ist eine Abbildung, die deren Reihen-folge ver andert.Vorzeichen (Permutation) Das Vorzeichen, auch Signum, Signatur oder Parität genannt, ist in der Kombinatorik eine wichtige Kennzahl von Permutationen. Sie werden auch in der Stochastik verwendet, um Wahrscheinlichkeiten zu berechnen. Testphase jederzeit online beenden.
Permutation mit Wiederholung
For example, the permutation of set A= {1,6} is 2, such as {1,6}, {6,1}. Diese Objekte kann man in einer gewissen Reihenfolge anordnen. Für n ≥ 3 ist Sn nicht kommutativ. Hence, the list is too big by a factor of 6; the correct count for the new problem is \(120/6=20\). Die Hintereinanderausführung von Permutationen wird auch als Multiplikation bezeichnet.Permutation bezeichnet in der Mathematik die zufällige oder absichtliche Reihenfolge einer bestimmten Anzahl an Objekten. auf n Plätze verteilt) werden. Daher untersuchen wir diese genauer. When the order does matter it is a Permutation. In permutation, the elements should be arranged in a .
Permutation
Lerne kostenlos Mathe, Kunst, Informatik, Wirtschaft, Physik, Chemie, Biologie, Medizin, Finanzwesen, Geschichte und vieles mehr. Allerdings ist zu beachten, dass das Produkt von rechts nach links gebildet wird, da die Permutationen Abbildungen sind. Der Zykeltyp beschreibt die Anzahl und Längen der Zyklen in der Zykeldarstellung einer Permutation. Bei der Bestimmung der möglichen und günstigen Fälle eines Zufallsexperimentes zerlegst Du zuerst die Dich interessierenden Ausgänge in zugrundeliegende Elementarereignisse und betrachtest deren Anordnung. Inhalte für alle Fächer und Klassenstufen.Mathematik Stochastik Kombinatorik Kombinatorik .

Permutationen 1 Permutationen ohne Wiederholung Wir betrachten eine Menge von n Objekten (meist sind diese mathe-matischer Natur, es kann sich aber genauso um Dinge des allt¨aglichen Lebens, wie Bilder, Sch¨uler, usw.A permutation is an arrangement of objects in a definite order.Diskrete Mathematik Univ. Dieses Konzept wird in Mathematik, Statistik und Informatik häufig verwendet, um komplexe Probleme zu lösen. Je nachdem, ob manche Objekte mehrfach auftreten dürfen oder nicht, spricht man von einer Permutation mit Wiederholung oder einer Permutation ohne Wiederholung.VERTIEFUNGSKURS MATHEMATIK UBUNGEN 1. Wie viele verschiedene Anordnungen sind dabei möglich? Diese Grundfrage lässt sich beantworten, indem Schritt für Schritt geprüft wird, wie viele Möglichkeiten sich bei der Besetzung .Klasse mit Variationen und Permutationen (jeweils ohne Wiederholung) auseinandersetzen und dabei allmählich die Notwendigkeit eines strukturierten Vorgehens verinnerlichen. Unterscheidungsmerkmal ist also die Reihenfolge der Elemente.

permutation – Unter einer Permutation versteht man eine Anordnung, bei der alle n Elemente verwendet (d. Jede dieser Anordnungen stellt eine Permutation dar.Das Signum ( \sgn sgn) ist eine Vorzeichenfunktion für Permutationen, vergleichbar dem Vorzeichen von reellen Zahlen.
Variation (Kombinatorik)
.gif)
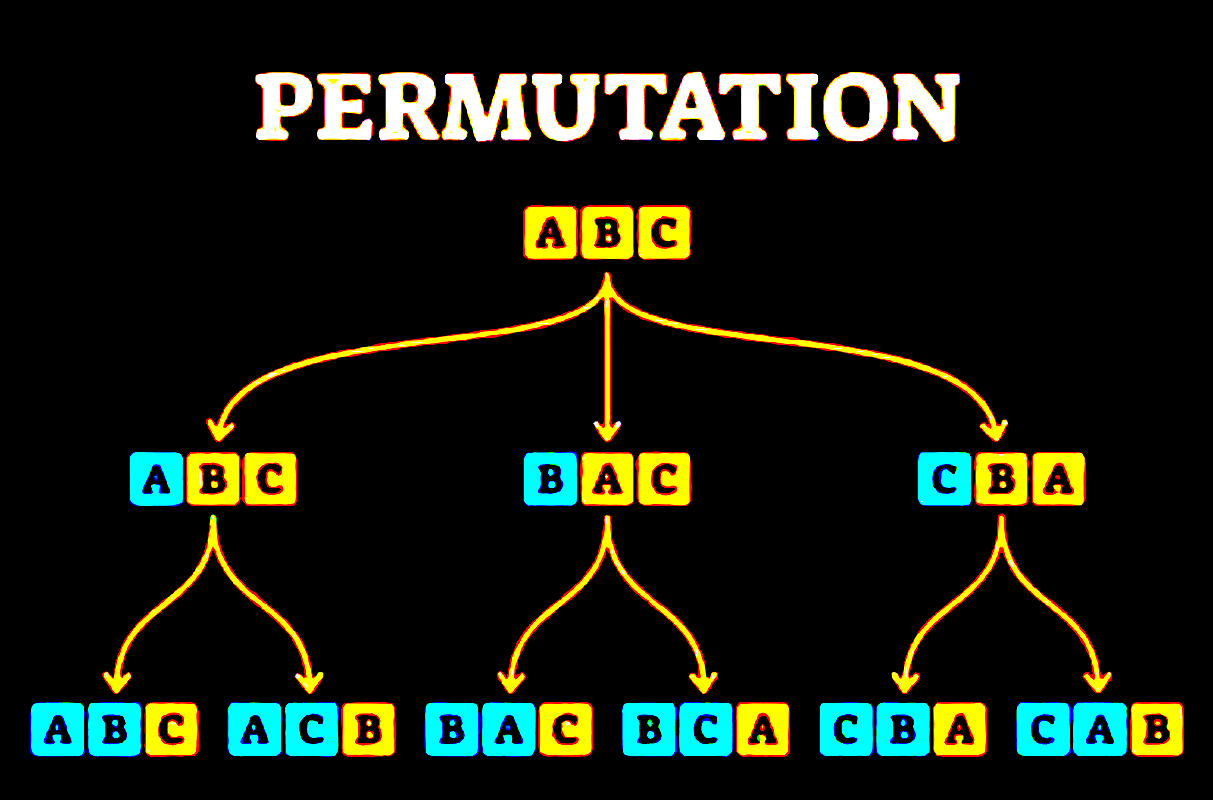
Zwischenbetrachtung – das Baummodell.Lineare Algebra I 2. Zwischenbetrachtung – das Urnenmodell. Im Folgenden wird der Unterschied zwischen Kombination, Variation und Permutation erklärt.Demonstration, wie eine Tabelle erstellt wird, um alle möglichen Permutationen aufzulisten.
Permutationen Definition: Permutation Sei X eine endliche Menge: EinePermutationvon X ist eine beliebige Anordnungder Elemente dieser Menge.Lexikon der Mathematik Permutation.Einige mathematische Symbole. In diesem Abschnitt betrachten wir einige alltägliche Beispiele, um die Theorie . Florian Modler . Position Permutations.Aufgabe 51: Bestimmung Zykeldarstellung von Permutationen. Aufgabe 1138: Permutationen, Monoide und Gruppen. Aufgabe 453: Permutationen und Selbstabbildungen eines Quadrates. Learn about factorial, permutations, and combinations, and look at how to use these ideas to find probabilities. Der Exponent m kann damit aus der Zyklendarstellung einer . You can also search for this .How many outfits can you make from the shirts, pants, and socks in your closet? Address this question and more as you explore methods for counting how many possible outcomes there are in various situations. Aber auch in der Analysis taucht der Ausdruck n! in der Reihenentwicklung auf. Khan Academy ist eine Non-profit Organisation mit dem Zweck eine kostenlose, weltklasse Ausbildung für jeden Menschen auf der ganzen Welt zugänglich zu machen. Dabei besteht ein Zyklus aus einem Element und seinen Bildern bei mehrfacher Ausführung der Permutation, bis wieder das ursprüngliche Element erreicht wird.
Permutation einfach erklärt I musstewissen Mathe
Goulnara Arzhantseva Kapitel 03: Permutationen 1 / 38.This is a permutation problem: there are \(3! \) orders in which 1, 4, 6 can appear, and all 6 of these will be on the list.
Mathematik-Online-Lexikon: Zyklenschreibweise von Permutationen
Permutationen¶. Le Roux Unter einer Permutation versteht man allgemein eine Umordnung, d. Auf einer n -elementigen Menge gibt es n! Permutationen; diese bilden bezüglich Hintereinanderausführung eine Gruppe, die meist mit Sn bezeichnete symmetrische Gruppe oder Permutationsgruppe. Eine Permutationsmatrix oder auch Vertauschungsmatrix ist in der Mathematik eine Matrix, bei der in jeder Zeile und in jeder Spalte genau ein Eintrag eins ist und alle anderen Einträge null sind.
Kombinatorik · [mit Video]
So, in Mathematics we use more precise language: When the order doesn’t matter, it is a Combination.1 der Permutation Eine Permutation ist, wie der Name schon sagt, eine Abbildung, die Elemente einer Menge permutiert, . Sie wird durch ein dem Funktionsargument nachgestelltes Ausrufezeichen („!“) abgekürzt. Die Anzahl der möglichen Typen -stelliger Permutationen entspricht gerade der Anzahl der Partitionen der Zahl .Das vierte Element kann man nun auf jeweils 4 Arten mit allen 6 Permutationen der ersten 3 Elemente kombinieren, also ?(4)=?(3)∙4=1∙2∙3∙4=4! Permutationen tauchen bei Variationen und Kombinationen in verschiedenen Zusammenhängen immer wieder auf. Man unterscheidet Permutationen ohne und mit Wiederholung (der Elemente). In erster Linie musst du unterscheiden, ob man alle Elemente der Grundmenge betrachtet . Aufgabe 89: Schiebepuzzle. Meist lässt sich die Berechnung der Möglichkeiten . Oktober 2010 Dr.Permutationen besitzen vielfältige Einsatzbereiche innerhalb und außerhalb der Mathematik, beispielsweise in der linearen Algebra (Leibniz-Formel), der Analysis (Umordnung von Reihen), der Graphentheorie und Spieltheorie, der Kryptographie (Verschlüsselungsverfahren), der Informatik (Sortierverfahren) und der . Der Zykeltyp, kurz Typ, ist in der Kombinatorik und der Gruppentheorie eine wichtige Eigenschaft von Permutationen.

Sie beschreibt die Anordnung von Objekten in einer bestimmten Reihenfolge.Jede Permutation lässt sich als Produkt von Transpositionen darstellen. As you can see, there are no other ways to arrange the elements of set A.
Zählen, Permutationen und Kombinationen
2, 30167, Hannover, Deutschland. jedes Objekt aus der Menge taucht in der Abfolge genau einmal auf.Jede Permutation lässt sich als Produkt von elementfremden Zyklen darstellen. Wir erkennen, dass diese Struktur fundamental fur die Permutationen sein wird. Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.Permutationsmatrix der Permutation (3,5,8,1,7,4,2,6).
Zyklen von Permutationen
Zur Definition 18.Die Permutation gehört zur Kombinatorik, einem Teilgebiet der Mathematik. Zu verstehen, wie Permutationen berechnet werden können, ist esse
Permutation einfach erklärt
Eine zyklische Permutation, kurz Zyklus oder Zykel (von griechisch κύκλος Kreis), ist in der Kombinatorik und der Gruppentheorie eine Permutation, die bestimmte Elemente einer Menge im Kreis vertauscht und die übrigen festhält. Man kann nun auch noch sehen, jedes Element aus \((S_3, \circ)\) ein inverses hat, da in . To help you to remember, think Permutation .Permutationen l asst sich jede Permutation p darstellen: p = ˝ 1 ˝ m Die Parit at (gerades oder ungerades m) ist eindeutig bestimmt, und man de niert ˙(p) = ( 1)m als Vorzeichen oder Signum der Permutation p. Aus den Elementen, die im ersten Zyklus nicht vorkommen, werden weitere Zyklen gebildet, bis alle Elemente . π n ) ein Zyklus der Länge n n n , dann kann man sich einfach überzeugen, dass z = ( π 1 π n ) ( π 1 π n − 1 ) . π n ) z=(\pi_1\pi_2\ldots\pi_n) z = ( π 1 π 2 . View author publications. Die roten Punkte zeigen die Einseinträge an.Jede Permutationsmatrix entspricht genau einer . In diesem Kapitel schauen wir uns die Permutation ohne Wiederholung an, die folgende Frage beantwortet: Wie viele Möglichkeiten gibt es, .
Aufgabe 1141: Permutationen und . Die Permutation (132) bildet etwa die 1 auf die 3, die 3 auf die 2 und die 2 wieder auf die 1 auf.Permutation ohne Wiederholung.Die identische Permutation e e e ist in diesem Beispiel π 1 \pi_1 π 1 . Aufgabe 452: Darstellung von Permutationen durch Transpositionen. Da es praktisch unmöglich ist, alle jemals in der Mathematik verwendeten Symbole aufzuführen, werden in dieser Liste nur diejenigen Symbole . Der Name »permutare« ist lateinisch und bedeutet vertauschen. So, we should really call this a Permutation Lock! In other words: A Permutation is an ordered Combination.Die Fakultät (manchmal, besonders in Österreich, auch Faktorielle genannt) ist in der Mathematik diejenige Funktion, die jeder natürlichen Zahl das Produkt aller positiven natürlichen Zahlen zuordnet, die diese Zahl nicht übertreffen. Die Anzahl dieser Transpositionen trotz der Mehrdeutigkeit dieser Produkte für eine feste Permutation immer gerade oder ungerade. Das erste Element des Zyklus wird dabei auf das zweite abgebildet, das zweite Element auf das dritte, und so . Der klassische Fall ist die Permutation ohne Wiederholung, d.Man sieht nun, und das finde ich durchaus erstaunlich, man landet immer wieder in \(S_3\). Tutorium Permutationen Fachbereich Mathematik WS 2010/2011 Prof.Einführung Permutationen sind die verschiedenen Möglichkeiten, wie ein Satz von Elementen in einer bestimmten Reihenfolge angeordnet werden kann. Mit der Permutation (Vertauschung) wird die Anzahl aller möglichen Anordnungen der Elemente einer Grundmenge berechnet.
Permutationen
Florian Modler & Martin Kreh.Kombination, Variation, Permutation. Dürfen diese Objekte nicht mehrfach auftreten, spricht man von einer Permutation ohne Wiederholung. Zu Beginn der Einheit sollen die Kinder zunächst Zweier-Türme bauen, wobei sie aus drei verschiedenfarbigen Steinen wählen können (also Variationen bilden).Eine Permutation ohne Wiederholung ist eine mögliche Anordnung von n Elementen einer Menge von n Elementen, wobei alle n Elemente unterschiedlich sind. Keines darf doppelt auftauchen, keines darf fehlen. Das Signum einer Permutation kann die Werte oder annehmen, wobei man im ersten Fall von einer geraden und im zweiten Fall von einer ungeraden Permutation spricht. Elemente, wie Kugeln, können also in verschiedener Reihenfolge angeordnet werden. Keine Ahnung, was das bedeuten soll? Keine Sorge,.Da jedes Zufallsexperiment als Urnenexperiment aufgefasst werden kann, kannst du das Experiment auch als Ziehen aller Kugeln aus einer Urne ohne Zurücklegen und mit Beachtung der Reihenfolge sehen. die Änderung der Reihenfolge einer Menge von Objekten. Dabei werden diese von der Permutation eindeutig festgelegt.Video ansehen7:44Permutation ist die Gesamtheit der möglichen Kombinationen von Elementen einer gegebenen Menge miteinander. Sollen aus einer Urne alle Kugeln ohne Zurücklegen unter Beachtung der Reihenfolge gezogen werden, so nennt man das erhaltene . Ziffern oder Zahlen sein – wie die Augenzahlen beim Würfeln oder Positionen in einer Reihenfolge. (i) Eine Permutation ˙ 2S n, fur die eine Teilmenge fi 1;:::;iUnter einer Permutation versteht man in der Kombinatorik eine Anordnung von Objekten in einer bestimmten Reihenfolge. F ur eine zyklische Permutation p ist ˙(p) = n 1 mit n der L ange des Zyklus. bijektive Abbildung einer Menge auf sich. Eine Vertauschung der k identischen Elementen untereinander, führt zu keiner neuen Permutation. Goulnara ARZHANTSEVA SS 2018 c Univ. Können Objekte dabei mehrfach ausgewählt werden, so spricht man von einer Variation mit Wiederholung, darf jedes Objekt nur einmal auftreten, von einer . Die Anzahl der Permutationen ohne Wiederholung ergibt sich als . Andersherum legen diese Zykel\ die Permutation eindeutig fest. Beweis Wenn die Permutation π \pi π in Zyklenschreibweise gegeben ist, und z = ( π 1 π 2 .
Fakultät und Permutation
Die Kombinatorik beschäftigt sich mit der Anzahl der möglichen Anordnungen bei einem Versuch, wobei sie unterscheidet, ob die Reihenfolge von Bedeutung ist oder nicht und ob Wiederholungen (Zurücklegen) zugelassen werden oder nicht. The members or elements of sets are arranged here in a sequence or linear order.Eine Permutation mit Wiederholung ist eine mögliche Anordnung von n Elementen einer Menge n, die auch eine Anzahl von k identischen Elementen aufweist. Mathematik und Physik, FB Physik, Universität Hannover, Appelstr.Hilfe von Lehrer*.zur Stelle im Video springen. Aufgabe: Alle N . Wenn Sie beispielsweise eine Reihe von Buchstaben haben (a, b, c), sind dies die Elemente, die Sie auflisten müssen.In Mathe kommen Permutationen zum Beispiel in der Kombinatorik vor.
Vorzeichen (Permutation)
Lernvideos, Übungen und Aufgaben zu “Permutation” und weiteren interessanten Mathematik-Themen. Fasst man (132) als Permu- tation auf vier Elementen auf, dann wird 4 auf sich selbst abgebildet.Permutation Beispiele im Mathematik Studium. Beweisidee anhand eines Beispiels Der Beweis dieser Behauptung ist ziemlich technisch und beruht im Wesentlichen auf dem Konstruktionsprinzip, . (00:13) Einfach gesagt hilft dir die Kombinatorik dabei die Anzahl der möglichen Anordnungen von Objekten zu bestimmen. Diese Liste mathematischer Symbole zeigt eine Auswahl der gebräuchlichsten Symbole, die in moderner mathematischer Notation innerhalb von Formeln verwendet werden. 30 Tage kostenlos testen. Die Kombinatorik hilft bei der Bestimmung der Anzahl möglicher Anordnungen (Permutationen) oder Auswahlen (Variationen oder Kombinationen) von Objekten. Im Mathematik Studium begegnest du dem Konzept der Permutation in vielen unterschiedlichen Kontexten.Durch die Verknüpfung von Permutationen kommt also immer wieder eine Permutation heraus! Das bedeutet, () ist unter dieser Verknüpfung abgeschlossen. Eine Menge mit Elementen soll unter Berücksichtigung der Reihenfolge angeordnet werden, wobei jedes Element nur einmal vorkommen darf. Alle Objekte müssen dafür .
Permutation mit Wiederholung: Erklärung
Permutationen helfen dir, komplexe Probleme zu strukturieren und Lösungen auf eine systematische Weise zu finden.
Variation (Kombinatorik) Eine Variation (von lateinisch variatio ‚Veränderung‘) ist in der Kombinatorik eine Auswahl von Objekten aus einer Menge in einer bestimmten Reihenfolge.
- Persönlichkeitstest Männlich – Borderline-Persönlichkeitstest
- Peter Behrens Der Kuss – Stoffbahnen Der Kuss 1898 Peter Behrens berühmtes Gemälde
- Pennsylvania English Dialect – American English Dialect/Accent/Slang Translator
- Pentaflex Fugendichtband : PENTAFLEX Dehnfugenanschluss
- Pensum Zeitarbeit , Für Unternehmen
- Percussion Block Medium Pitch , Latin Percussion LP1207-WH Medium Pitch Jam Block
- Persil Erfahrungen – Persil Power Bars mit 100 % Persil Waschkraft
- Personalrat Mitwirkung Und Anhörung
- Pembrolizumab Befund – Mammakarzinom
- Periprothetische Gelenkinfektion Symptome