Neural Networks Approximation : Deep Networks for Tensor Approximation

Di: Samuel

Neural Network Approximation of Refinable Functions Abstract: In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. For any sufficiently .Universal Approximation Theorem # The XOR function is merely an example showing the limitation of linear models. The support for a .According to the Universal Approximation Theorem, a neural network with a single hidden layer can do exactly that.

Why Neural Nets Can Approximate Any Function

Based on rapidly exploring random trees (RRT), we propose an incremental sampling-based motion planning algorithm, i. Coarse-scale surrogate models in the context of numerical homogenization of linear elliptic problems with arbitrary rough diffusion coefficients rely on the efficient solution of fine-scale sub-problems on . A three-hidden-layer neural network with super approximation power is introduced. The expressive power of neural networks: A view from the width. By now, there exists a variety of results which show that a wide range .Spectral Barron space and deep neural network approximation. In: Advances in Neural Information Processing Systems, vol.

Neural Networks, the Universal Approximation Theorem and Option ...

understanding of the internal mechanism of convolutional neural networks.Unfortunately, existing methods either focus on verifying a single network or rely on loose approximations to prove the equivalence of two networks.For smooth functions, we show in Theorem 1. These networks are very sim- ilar, and their architecture is shown in Figure 1.This paper focuses on developing effective computational methods to enable the real-time application of model predictive control (MPC) for nonlinear systems.The neural network enables us to construct the constitutive relation based on both macroscopic observations and atomistic simulation data. Computers & Math. In the system, only the system output is available at sampling instants. We first describe how to approximate univariate polynomials of any degree with tanh neural networks. We prove the sharp embedding between the spectral Barron space and the Besov space. One of the classical results for neural networks is the universal approximation property (UAP) of shallow networks [10, 1, 20], i. In real-life problems, we do not know the true regression function, which can be (highly) nonlinear in many situations.A neural network is a group of interconnected units called neurons that send signals to one another. We provide notions of interpretability based on approximation theory in this study.The notion of neural network approximation spaces was originally introduced in , where \(\Sigma _n\) was taken to be a family of neural networks of increasing complexity.Neural network approximation of coarse-scale surrogates in numerical homogenization. We show that standard multilayer feedforward networks with as few as a single hidden layer and arbitrary bounded and nonconstant activation function are universal approximators with respect to L p (μ) performance criteria, for arbitrary finite input environment measures μ, provided only that sufficiently many hidden units are available. We first implement this approximation interpretation on a specific . The main difference between the two types of net- work is in the functions calculated at the hidden nodes. This article surveys the known approximation properties . Opschoor∗ Philipp C.Neural Networks Two types of networks are discussed in this paper: the multilayer perceptron (MLP) and the radial basis function (RBF) network.Graph Neural Networks (GNNs) are one of the best-performing models for processing graph data. While tensor splines are supported on orthants, aligned with the coordinate axes, this does not hold true for neural networks. The purpose of Section VIII is to demonstrate that function: An approximation by neural networks with a fixed weight. It is widely believed that deep neural network models are more accurate than shallow .edu Boris Hanin bhanin@princeton. Because of the great capabilities of MLP as a universal approximator, it has received significant attention in recent years. To train the deep neural network offline, we propose a new . Neural Networks 16, 24–38 (2005) Article Google Scholar Funahashi, K. Note that ReLU networks are in fact piecewise linear functions, so they have at most nonzero. Fabian Kröpfl, Roland Maier, Daniel Peterseim. Specifically, we build the approximation network . We consider the simple but representative setting of using continuous-time linear RNNs to learn from data generated by linear relationships.edu Neural Networks (NNs) are the method of choice for building learning algo-rithms.

Every Machine Learning Algorithm Can Be Represented as a Neural Network ...

Neural Network Approximation Based Multi-dimensional Active Control of Regenerative Chatter in Micro-milling Download book PDF. In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. We introduce the p th order central finite difference operator δ h p for any f ∈ C p + 2 ( [ a, b]) for some p ∈ N by (15) δ h p [ f] ( x) = ∑ i = 0 p ( − 1) i p i f x + p 2 − i h. This algorithm aims to solve motion planning problems .

Deep Neural Network Approximation using Tensor Sketching

As mentioned earlier, is a linear subspace of . Long Beach: Neural Information Processing Systems Foundation, 2017, . Due to overly conservative approximation, differential verification lacks scalability in terms of both accuracy and computational cost. Prior work can approximate the non-linear operations with piecewise linear (PWL) function, but such approximation neglects considering the hardware . Proof: Let be the set of neural networks.Keywords: Neural network, Approximation theory, Deep learning, GAN MSC codes: 41A25, 62G08, 68T07 1 Introduction The expressiveness and approximation capacity of neural networks has been an active research area in the past few decades.Approximation by Neural Networks with Sigmoidal Functions 2015 As we know, in the usual approximation by polynomials, for any f ∈ C( −1,1]), there is a polynomialP n(x)ofdegreen such that f − P n = O ω f, 1 n.In recent years, functional neural networks have been proposed and studied in order to approximate nonlinear continuous functionals defined on \(L^p([-1, 1]^s)\) for integers \(s \ge 1\) and \(1\le p<\infty \). a neural network with one hidden layer can ap-Our purpose in this paper is to construct three types of single-hidden layer feed-forward neural networks (FNNs) with optimized piecewise linear activation functions and fixed weights and to present the ideal upper and lower bound estimations on the approximation accuracy of the FNNs, for continuous function defined on bounded .In this paper, the problem of near-optimal motion planning for vehicles with nonlinear dynamics in a clustered environment is considered. The collection of neural networks forms a systematic model thanks to their universal approximation property.In this work we design graph neural network architectures that capture optimal approximation algorithms for a large class of combinatorial optimization problems using powerful algorithmic tools from semidefinite programming (SDP). Shiva Prasad Kasiviswanathan, Nina Narodytska, Hongxia Jin. In this paper, we study a fundamental .

Approximation by Neural Networks with Sigmoidal Functions

The approximation of non-linear operation can simplify the logic design and save the system resources during the neural network inference on Field-Programmable Gate Array (FPGA).Weprovethatforanalytic functionsin low dimension, theconvergencerateof thedeepneural network approximation is exponential.The lack of interpretability has hindered the large-scale adoption of AI technologies.The “neural networks” studied in differ from standard usage [5, 7,8,9, 14] in the sense of ; they are defined as a linear combination of neural networks whose weights are fixed in advanced and approximation is in the sense of finding the coefficients of such linear combinations. However, [ 10 ] does not impose any restrictions on the size of the individual network weights , which plays an important role in practice and which is . To prove that is dense in , we . Mathemat- ically, the latter can be . Theorem 1 If the in the neural network definition is a continuous, discriminatory function, then the set of all neural networks is dense in .Single hidden layer feedforward neural networks (SLFNs) with fixed weights possess the universal approximation property provided that approximated functions are univariate.Neural Network Approximation of Refinable Functions.This study considers an adaptive neural-network (NN) periodic event-triggered control (PETC) problem for switched nonlinear systems (SNSs).Exponential ReLU Neural Network Approximation Rates for Point and Edge Singularities Carlo Marcati∗ Joost A. 47, 1897–1903 .

Approximation capabilities of multilayer feedforward networks

But this phenomenon does not lay any restrictions on the number of neurons in the hidden layer. And some applications of these frameworks are given, including tensor rank approximation [ 47 ], video snapshot compressive imaging (SCI) [ .LaPlace Approximation. View PDF Abstract: We present a numerical algorithm that allows the approximation of optimal controls for stochastic reaction-diffusion equations . Overview of Neural Networks. Neurons can be either biological cells or mathematical models.In the following content of this section, we will introduce these three different frameworks for tensor approximation in detail, namely, classical deep neural networks, deep unrolling, and deep PnP.Deep Neural Network Approximation using Tensor Sketching. Their popularity stems from their empirical success on several challenging learning problems. Google Scholar Lu Z, Pu H, Wang F, et al.View a PDF of the paper titled Neural Network Approximation of Optimal Controls for Stochastic Reaction-Diffusion Equations, by Wilhelm Stannat and Alexander Vogler and Lukas Wessels .: On the approximate realization of continuous mappings by neural networks.In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. They are known to have considerable computational complexity, despite the smaller number of parameters compared to traditional Deep Neural Networks (DNNs).1 that deep ReLU networks of width O(N log N) and of depth O(L log L) can achieve an approximation rate of O(N 2(s 1)=dL 2(s 1)=d) with respect to the W1;p([0; 1]d) norm.However, the approximation by neural networks with \(\text {ReLU}^{k}\) functions is substantially different from tensor splines, which would serve as analog for splines in higher dimension. 1 Introduction The approximation properties of deep neural network models is among the most tantalizing problems in machine learning. Given the spectral Barron space as the target function space, we prove a dimension-free result that if the neural network contains L hidden layers with N .We are now ready to present the Universal Approximation Theorem and its proof.

Tansig and F 3 s based neural networks function approximation goodness ...

They are now being investigated for other numerical tasks such as solving high dimensional partial di erential .edu Guergana Petrova gpetrova@math.

(a) Architecture of a feedforward neural network. (b) Examples of ...

Neural Network Approximation Based Multi-dimensional Active Control of Regenerative Chatter in Micro-milling . Operations-to-parameters ratio for GNNs can be tens and hundreds of times . In neuroscience, a biological neural network is a .

On the approximation of functions by tanh neural networks

Xiaoli Liu 16, Chun-Yi Su 16,17 & Zhijun Li 16 .1 Network architecture. Petersen† Christoph Schwab∗ October 19, 2020 Abstract We prove exponential expressivity with stable ReLU Neural Networks (ReLU NNs) in H1(Ω) for weighted analytic function classes in certain polytopal domains . First made popular by David MacKay’s paper in 1992, when he applied the LaPlace approximation to Bayesian neural networks, the method has seen a combeback in recent years with researchers showing their applicability to today’s deep neural networks.

LaPlace Approximation for Deep Neural Networks

Neural Network Approximation Ronald DeVore rdevore@math. A novel adaptive law and a state observer are constructed by using only the sampled system output.

Best k

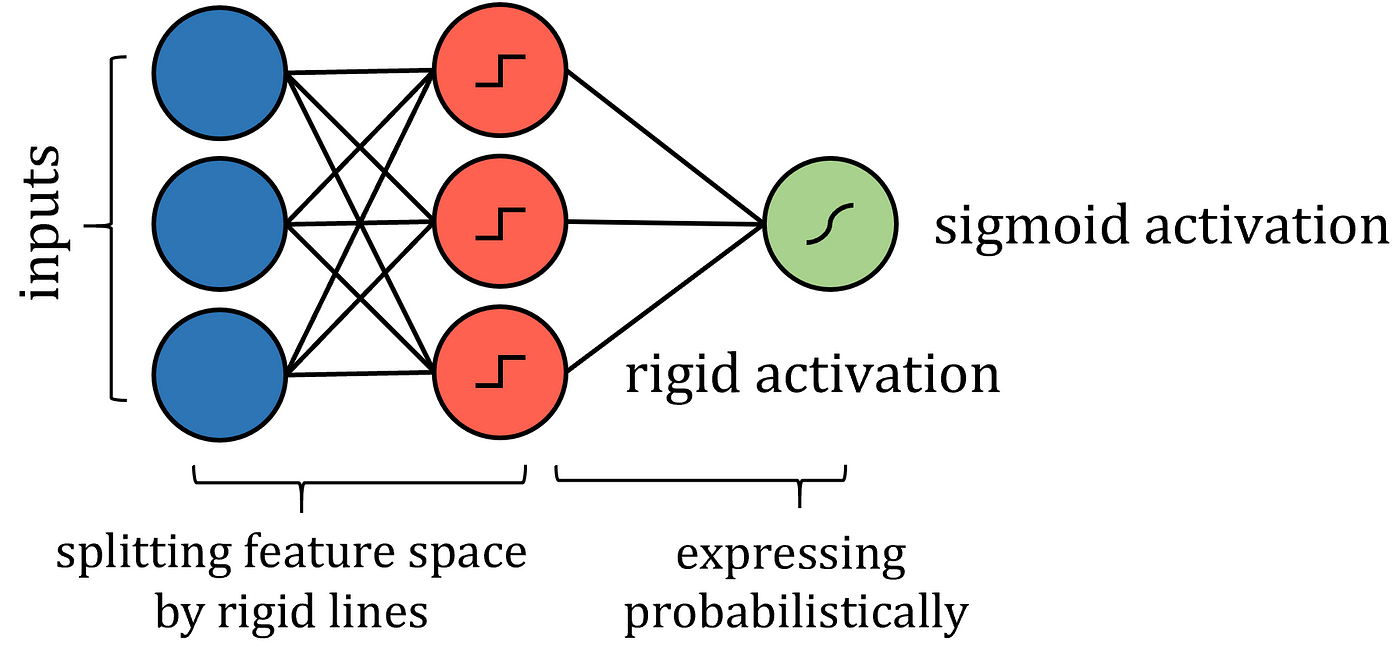
The more this number, the more the probability of the . For our purposes, we will be looking only at fully connected neural networks with an input layer, a single hidden layer, and an output layer.Why deep neural networks for function approximation? ArXiv:1610.Univariate polynomials. The purpose of Section VIII is to demonstrate that function

[PDF] Neural network approximation

The Universal Approximation Theorem for Neural Networks

deep neural networks over shallow neural networks have been demonstrated in a sequence of depth separation results; see e.

Deep Networks for Tensor Approximation

In the following context, we mainly review the existing works closely related to this paper. [16, 52, 54, 13] Compared to a vast number of theoretical results on neural networks for approximating functions, the use of neural networks for expressing distributions is far less understood on the theoretical side. Neural Networks 2, 183–192 (1989) Article Google Scholar Hahm, N. Deep neural networks are powerful learning models that achieve state-of-the-art performance on many computer vision, speech, and language processing tasks. The universal approximation property of shallow neural networks with one hidden layer and various . Therefore, a natural problem is whether the term ω f,√1 n in (1. Neural networks (NNs) are the . The following paragraphs will explain the method and .4) can be replaced by ω f,1 ? To answer this question, we introduce a .We study the approximation properties and optimization dynamics of recurrent neural networks (RNNs) when applied to learn input-output relationships in tem-poral data.

Visual and Rigorous Proof of Universal Approximation Theorem (UAT)

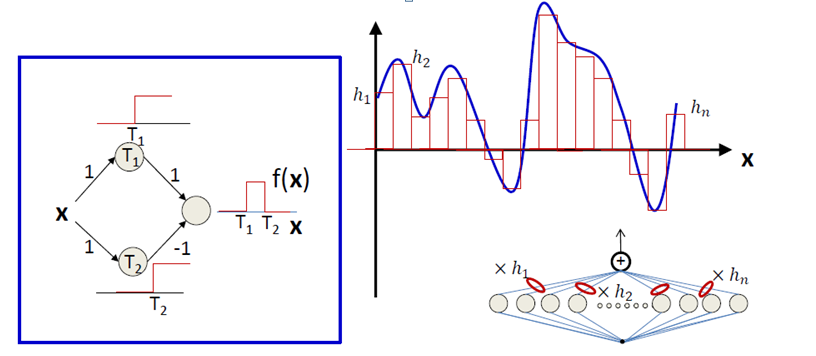
weight approximation in neural networks presented in Section VI. Yulei Liao, Pingbing Ming. While individual neurons are simple, many of them together in a network can perform complex tasks., near-optimal RRT (NoD-RRT).However, their theoretical properties are largely unknown beyond universality of approximation or the existing analysis does not apply to . In the case of our clothing size predictor, the input . In contrast to traditional deep learning models, this architecture is intrinsic symmetric, guarantees the frame-indifference and material-symmetry of stress. There are two main types of neural network. rst (weak) derivatives. Network examination based on spike training is necessary, so that this new architecture could be applied to study the capabilities of the spiking neural network in function approximation. We proceed, in Section VII, with the development of a method—termed the transference principle—for transferring results on function approximation through dictio-naries to results on approximation by neural networks.This article surveys the known approximation properties of the outputs of NNs with the aim of uncovering the properties that are not present in the more traditional methods of approximation used in numerical analysis, such as approximations using polynomials, wavelets, rational functions and splines. By now, there exists a variety of results which show that a wide range of functions can be approximated with sometimes .Neural Networks (NNs) are the method of choice for building learning algorithms. To overcome these problems, we propose NeuroDiff, a . This network is built with the floor function (⌊ x ⌋), the exponential function (2 x), the step function (1 x ≥ 0), or their compositions as the activation function in each neuron and hence we call such networks as Floor-Exponential-Step (FLES . However, most scholars agree that a convincing theoretical explanation for this success is still lacking. Download book EPUB. However, the fundamental idea of interpretability, as well as how to put it into practice, remains unclear. Concretely, we prove that polynomial-sized message passing algorithms can represent the most .

Deep Neural Network Approximation Theory

To achieve this goal, we follow the idea of approximating the MPC control law with a Deep Neural Network (DNN).

BAHTMZ

General