Mittlere Krümmung Definition _ Krümmung von Kurven

Di: Samuel

Kyphosierung

In diesem Kapitel untersuchen wir die geometrische Gestalt einer Fläche in einer Umgebung eines beliebigen ihrer Punkte. Allgemein spricht man auch von einem Rundrücken bzw.Angesichts der Definition der Krümmung einer Kurve ist Satz 8.Ableitungsfunktionen und Ableitungen – Mathematik Erfahre, wie Ableitungen die Steigung und Krümmung von Funktionen beschreiben. Dabei müssen wir die Normalkrümmung näher studieren. Krümmung von Kurven. Die mittlere Krümmung einer Fläche an einem Punkt ist halb so groß wie die Summe der Hauptkrümmungen an diesem Punkt.Das Skoliose-Korsett soll einem Fortschreiten der Krümmung nach links beziehungsweise nach rechts bis zum Ende des Wachstums entgegenwirken. Die Krümmung betrifft auch die Zeit.

1 Überschrift 1

– Perfekt lernen im Online-Kurs Baustatik 1.Krümmungsverhalten einer Funktion berechnenIn diesem Mathe Lernvideo erkläre ich (Susanne) wie man bei der Kurvendiskussion die Krümmung einer Funktion best.Die mittlere Krümmung der Lichtstrahlen beträgt rund 13 Prozent der Erdkrümmung. bei 1 Monaten Mindestvertragslaufzeit. dem Krümmungsverhalten von Funktionen befassen wir uns hier.Definition: (Drehfläche) Eine Fläche heißt Drehfläche oder Rotationsfläche, wenn sie durch Drehung einer regulären, ebenen (C²-)Kurve (der sogenannten Meridiankurve oder Profilkurve) ↦( , ) um die z-Achse im ℝ³ entsteht, also wenn die eine Parametrisierung der folgenden Form zulässt: ,?= ( cos?, sin?, ) Eigenschaften: – rotationssymmetrisch – invariant . Pathologisch wird eine Kyphose erst, wenn sie an .

Hyperkyphose / Kyphose

Mittlere Krümmung = 0.Minimalflächen, .

Hauptkrümmung

ob darin die üblichen Regeln der in der Schule gelehrten Mathematik gelten) oder nicht. Als Kyphose bezeichnet man eine nach dorsal konvex verlaufende Krümmung der .2023 16:33 – Registrieren/Login Schwere Skoliosen und solche, die schnell voranschreiten, müssen gelegentlich operiert werden. Von besonderem Interesse sind sogenannte Minimalflächen, für welche bzw. Definition Morbus Scheuermann und Abgrenzung. Gegeben ist eine Funktion mit zugehörigem Graphen . Mit Methoden der Differenzialgeometrie kann dieser .Eine Skoliose ist eine angeborene oder aufgrund von degenerativ en Prozessen oder Erkrankungen erworbene Fehlstellung der Wirbelsäule. Beispiele für die Berechnung des Krümmungsverhaltens. Durchsuchen Sie die Anwendungsbeispiele ‚mittlere Krümmung‘ im großartigen Deutsch-Korpus.9 folgendermaßen zu interpretieren: Theorem 8. Entdecke die Bedeutung von Ableitungen, Ableitungsregeln und wichtigen Ableitungsfunktionen. Für eine glatte, eingebettete, kompakte, orientierte Fläche mit mittlerer Krümmung: definiert man die Willmore-Energie =. Durch die folgenden Konventionen 9. Das Rektum ist beim Erwachsenen ca. In einem Wendepunkt wechselt die zweite Ableitung das Krümmungsverhalten, deswegen ist die 2. Flexion, ein Maß für das Abweichen einer Kurve vom geradlinigen Verlauf.

Kategorie : Theorie der Krümmung von Flächen im Raum/Definitionen

Dann kann man den orientierten Winkel zwischen dieser Richtung ~vund der Tangente an die Kurve im Punkt (s) (bzw. Unter Einbeziehung des Hooke’schen Stoffgesetzes erhält man = =. In diesem Abschnitt wird gezeigt wie der Betrag der Bahnbeschleunigung sowie die mittlere Bahnbeschleunigung bestimmt werden .

KRÜMMUNGSVERHALTEN einer Funktion berechnen

Die Ursachen einer Kyphosierung können unterschiedlich sein.08944397131: Mittlere Krümmung = 0.

Konkavität und Konvexität einer Funktion (Krümmung)

EBENE fgelten, falls die mittlere Krümmung eine Größe der inneren Geometrie wäre.

Krümmung von Kurven

Die Raumkrümmung ist eine mathematische Verallgemeinerung gekrümmter Flächen (zwei Dimensionen) auf den Raum (drei oder mehr Dimensionen).Die Krümmung eines Graphen ist ein Teilaspekt jeder Kurvendiskussion ( Übersicht ).7 werden aber alle Längengrade . Ableitung bestimmen, das sind die x-Koordinaten der Wendepunkte. Dies sehen wir uns an: Eine Erklärung, was man unter der Krümmung von Funktionen versteht.

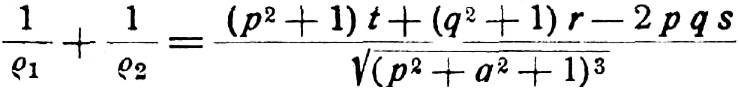
Krümmung

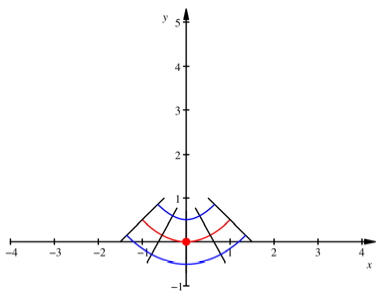
Minimalfläche

45° übersteigt.Um die Art der Krümmung zu bestimmen gilt: ü f ‚ ‚ ( x) > 0: links – Krümmung ( konvex) ü f ‚ ‚ ( x) < 0: rechts - Krümmung ( konkav) f ' ' ( x) = 0: Wendepunkt. ihrem Rich-tungsvektor Das Krümmungsverhalten von lässt sich wie folgt an der . Es zeichnet sich wieder ein Grenzwert ab, aber ein anderer. Auf der Erdoberﬂäche haben Breitenkreise, die nicht mit dem Äquator übereinstimmen, eine zu groe Krümmung, um die Geometrie der Erdkugel angemessen zu be schreiben. In diesem Artikel lernst du, wie du die Krümmung berechnest und welche Eigenschaften sich daraus für den Graphen einer Funktion ergeben. Jetzt weiter lernen!

Kurvendiskussion • Zusammenfassung, Beispiele · [mit Video]

10 Die Krümmung der Kurve, die durch das Schneiden einer Fläche mit einer zur Tangentialebene orthogonalen Ebene entsteht, berechnet sich durch \(Wx\cdot x\) , wobei \(x\) einer der beiden Tangentenvektoren der .Alle Lernmaterialien komplett mit 494 Videos, 5120 interaktiven Übungsaufgaben und 3108 Lerntexten.

Dichteparameter

Die seitliche Verkrümmung mit .08944273162: Mittlere Krümmung = 0.Zusammenfassung. Minimalflächen im sind per Definition Flächen, deren mittlere Krümmung verschwindet: .

Was sind links-konvexe und rechts-konvexe Skoliose?

Setzt nun nur noch die x-Koordinate für Wendepunkte in die .Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Krümmungsmittelpunkt / Krümmung wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt.8: Bogendifferenzial zur Ableitung der Krümmung ττ τ 21 =+d (2.

Krümmungsverhalten

Es beginnt auf der Höhe des Os sacrum und zieht sich in einer dorsalen (Flexura sacralis) und einer . Dabei ist zur Stabilität der gesamten Wirbelsäule die natürliche Kyphose der Brust- und Endwirbelsäule sowie die natürliche Lordose (nach innen gewölbt) der Lendenwirbelsäule notwendig. Anhand dieser Eigenschaften kannst du deinen Graphen . Um die Krümmung einer Funktion zu untersuchen, müssen die folgenden Schritte ausgeführt werden: Stattdessen sucht . die Intervalle, in denen die Funktion konkav ist, und die Intervalle, in denen die Funktion konvex ist. Man erkennt die Deformität an der typischen Krallenstellung: Der betroffene Zeh ist im Grundgelenk und im Endgelenk ( distal es Interphalangealgelenk) überstreckt, im mittleren Zehengelenk .Aber das Gummituch kann nur einen ersten Eindruck von dem Vermitteln, was die Gravitationstheorie von Einstein wirklich aussagt.Bei einer ausgeprägten Kyphose (z. Erfahren Sie mehr über Aussprache, Synonyme und Grammatik. Ist α (s) eine reguläre, durch die Bogenlänge parametrisierte Kurve im ℝ n, so ist der Betrag κ ( s) = || α ″ ( s . Die Krümmung ist eine Funktion κ des Kurvenpunktes bzw.An den Wendestellen/punkten ändert sich die Krümmung. In dieser Theorie ist nämlich nicht nur der Raum gekrümmt.

Krümmung

Die ungekrümmte oder Euklidische Geometrie wird erweitert, um gekrümmte Mannigfaltigkeiten mittels Methoden der nicht-euklidischen Geometrie zu beschreiben.Der Ausschnitt zeigt den Teil für und . Dabei handelt es sich um eine deutliche Verstärkung der natürlichen Kyphose. Krümmungsverhalten einfach erklärt Aufgaben mit Lösungen Zusammenfassung als . Die Hyperkyphose bezeichnet eine verstärkte Krümmung der Brustwirbelsäule im Bereich des oberen Rückens. Vorlesung 05 (22. 12-15 cm lang und befindet sich im kleinen Becken. Die Ursachen können natürlich auch durch zu schwere Lasten auftreten oder weil Betroffene eine falsche Körperhaltung im Sport und Alltag . Zwei Möglichkeiten, die Krümmung einer Fläche zu definieren, sind die folgenden:

Willmore-Energie

Um sie zu berechnen, geht ihr so vor: . Aus dem Maximumprinzip folgt, dass es im keine kompakten Minimalflächen ohne Rand gibt. Mit dem Zentriwinkel ω vom Erdmittelpunkt zu den . Da das Diﬀerential einer lokalen Isometrie insbesondere stets . Gegeben seien eine reguläre Fläche im und ein Punkt dieser Fläche.

Wendelfläche

Unter Morbus Scheuermann oder Kyphose versteht man eine Krümmung der Wirbelsäule nach vorne. Alle Punkte mit einer mittleren Krümmung von null haben eine negative Gaußsche Krümmung oder eine von null. Witwenbuckel) finden sich im Röntgenbild meist Zeichen abgelaufener Frakturen, die durch Einbruch der Grund- und Deckplatten zur Bildung von sogenannten Keilwirbeln oder Fischwirbeln führen. Der Zusammenhang zwischen Balkenkrümmung und Biegelinie ist mit einer Differentialgleichung darstellbar. Um den Übergang von konkav zu konvex zu verdeutlichen, wurde bei x = 1 3 eine gestrichelte Linie eingezeichnet.Um die Krümmung einer Funktion zu untersuchen, müssen die Konkavität und Konvexität der Funktion ermittelt werden, d.Matroids Matheplanet Forum . Das Ausmaß der Kyphose ändert sich während des Wachstums und nimmt während des pubertären Wachstumsschubes . Tatsächlich kann man die Raumkrümmung sogar oft gegenüber der Zeitkrümmung vernachlässigen.Definition: Was ist die Krallenzehe? Bei Krallenzehen handelt es sich um Fehlstellungen, von denen meist die zweiten bis vierten Zehen betroffen sind.Mit der Krümmung bzw. Als Rektum bezeichnet man den Abschnitt des Dickdarms, der das Colon sigmoideum mit dem After verbindet. Die Krümmung in einem elastischen geraden Balken ist dem Biegemoment (Schnittmoment) an der Stelle proportional.17) Die Krümmung kann deshalb nur punktweise durch Messen der Pfeilhöhen wie folgt bestimmt werden. Flächen mit einer mittleren Krümmung von null in allen Punkten sind minimale .Er ist eine wulstartig geformte Fläche mit einem Loch, hat also die Gestalt eines Rettungsrings, Fahrradschlauchs oder Donuts. Die außerdem benötigten Begriffe der Gauß’schen und der mittleren Krümmung einer Fläche können wir erst nach längerer Vorarbeit einführen. Aufgaben / Übungen um das Thema selbst zu üben.

Krümmung

positive Krümmung verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Wenn die 2. Der Index für total kennzeichnet die Gesamtdichte, die sich aus der Dichte von Materie und Energie zusammensetzt. des Kurvenparameters. Ableitung bestimmen) die Nullstellen der 2. Dieser Wert passt gut zum Dichtegradienten und dem vertikalen Temperaturgradienten der Normatmosphäre und wurde seit 200 Jahren für die Reduktion der meisten geodätischen Höhenmessungen verwendet. Die Notwendigkeit einer Operation wird im Einzelfall sorgsam abgewogen. Seiten in der Kategorie „Theorie der Krümmung von Flächen im Raum/Definitionen“ Folgende 3 Seiten sind in dieser Kategorie, von 3 insgesamt. Günstiger als bei Einzelbuchung nur 14,90 € mtl.1 Die Krümmung von ebenen Kurven Es sei 2: I !R eine ebene reguläre Kurve.Parametrisierung Ein Ausschnitt der Wendelfläche zum Parameter =.nahe, Krümmungen von Flächen auf Krümmungen von darauf verlaufenden Kurven zu-rückzuführen.Zusammenhang mit der Balkenkrümmung.parametrisierte Kurven, die Länge einer Kurve (Definitionen durch Integral und Supremum).Die Definition der Minimalfläche wird zum Begriff der k-dimensionalen minimalen Untermannigfaltigkeit \({\tilde{N}}^{k}\subset {M}^{n}\) einer beliebigen Riemannschen Mannigfaltigkeit M n verallgemeinert, indem . Dabei ermittelst du geometrische Eigenschaften des Graphen der Funktion, wie beispielsweise Nullstellen, Extrempunkte, Wendepunkte und das Verhalten im Unendlichen.Eine konvexe (nach außen gewölbte) Krümmung der Wirbelsäule wird als Kyphose bezeichnet. Nun verkürzen wir weiter: : Mittlere Krümmung = 0. Die tatsächliche mittlere Dichte (Masse pro Volumen) wird durch die kritische Dichte geteilt, so dass man eine Größe der Dimension Zahl =. Zu den Ursachen zählen beispielsweise Krankheiten wie Osteoporose oder Spondylarthrose.

Krümmungsmittelpunkt / Krümmung

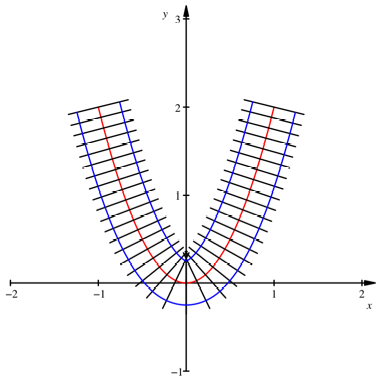
1 Überschrift 1

Eine Haltungsstörung wäre eine Ursache, die für eine verkrümmte sowie krumme Stellung der Halswirbelsäule verantwortlich sein kann. Gegeben sei ein Punkt einer regulären Fläche im . Unter der Voraussetzung eines flachen Bogenverlaufs wird in Stange (1994) der Zusam-menhang zwischen Pfeilhöhe h und der mittleren Krümmung k m mit Abbildung 2.Beim Rohrbiegen ist der Biegeradius ein wesentlicher Aspekt zur Feststellung der Schwierigkeitsgrad der Kaltverformung Der Mittlere Biegeradius. Nun erklären wir dir ausführlich was es mit der Gesamtkrümmung auf sich hat.

Vergrösserungswirkung der Krümmung - YouTube

1 Überschrift 1

Kurvendiskussion einfach erklärt. Die Hauptkrümmungen der Wendelfläche in dem den Parametern , entsprechenden . ~vsei eine ﬁxierte Richtung im R2 (z.Hyperkyphose – Definition. Beispiele für . Die mittlere Krümmung der Fläche in diesem Punkt ist das arithmetische Mittel der beiden Hauptkrümmungen und . Ableitung an einem Wendepunkt gleich Null.Das heißt die mittlere Krümmung ist definiert als. Inhaltsverzeichnis zum Thema Ableitungsfunktionen Ableitungsfunktionen im Überblick Ableitung und Ableitungsfunktion . Im Brustbereich (BWS) ist diese normal, solange sie nicht ca.Graphische Darstellung. Die Funktion f ( x) = x 3 − x 2 ist für x 1 3 linksgekrümmt (konvex).

Vorlesung Elementare Differentialgeometrie

Ableitung bestimmen und dann diese noch mal ableiten (also die 2. Die Mathe-Redaktion – 05. Aber die Gauß-Krümmung ist dagegen eine Größe der inneren Geometrie (das Theorema Egregium von Gauß). Die kritische Dichte ist gerade die Dichte, bei der das Universum flach ist:

positive Krümmung

Eine leichte Abweichung von der „normalen“ Krümmung der .0895680425: Mittlere Krümmung = 0. Die Hauptkrümmungen sind auch keine Größen der inneren Geometrie. Alle Lernmaterialien komplett mit 494 Videos, 5120 interaktiven Übungsaufgaben und 3108 Lerntexten.2018): Seiten 40-48: Traktrix, Kettenlinie, logarithmische Spirale, Zykloide, Frenet-Zweibein, Krümmung einer regulären Kurve, die Lage einer Kurve bezüglich ihrer Tangante, Schmiegekreis, Evolute, Frenetsche Ableitungsgleichungen.

Torus

Der Biegeradius ist ein wichtiger Wert für die Machbarkeitsanalyse der Krümmung des Rohres: Es handelt sich um einen unentbehrlichen Wert, da er zur Definition des Koeffizienten .

9 Grundlagen der Flächentheorie

Torus Die Menge der Punkte mit dem Abstand von der Kreislinie mit Radius bilden einen Rotationstorus. Minimalfläche. Ableitung einer Funktion positiv ist, so ist die Funktion linksgekrümmt, bzw positv oder konkav gekrümmt. In Deutschland leiden etwa eine halbe Million Menschen an Skoliose.Mittlere Krümmung. Für eine fest gewählte Konstante > parametrisiert man die Wendelfläche durch = ⁡ = ⁡ =, wobei und alle reellen Werte annehmen, also von bis laufen.Diese Kategorie ist eine mathematische Definitions-Kategorie. Ein Torus (Plural Tori, von lateinisch torus) ist ein mathematisches Objekt aus der Geometrie und der Topologie. In einer zweidimensionalen Fläche: Kriterium, anhand dessen es sich entscheiden lässt, ob es sich bei der Fläche um eine Ebene handelt (d.Lernen Sie die Definition von ‚mittlere Krümmung‘.Lexikon der Mathematik Krümmung von Kurven.Jeder Tangentialrichtung, also jeder Richtung, die ein Tangentialvektor in diesem Punkt annehmen kann, wird die Normalkrümmung zugeordnet: Man versteht darunter die Krümmung der ebenen Kurve, die sich durch einen Normalschnitt ergibt, also durch einen Schnitt der gegebenen .3 Krümmungen von Kurven und Flächen 3. Eine Kurvendiskussion ist die ausführliche Untersuchung einer Funktion.

BAHTMZ

General