BAHTMZ

General

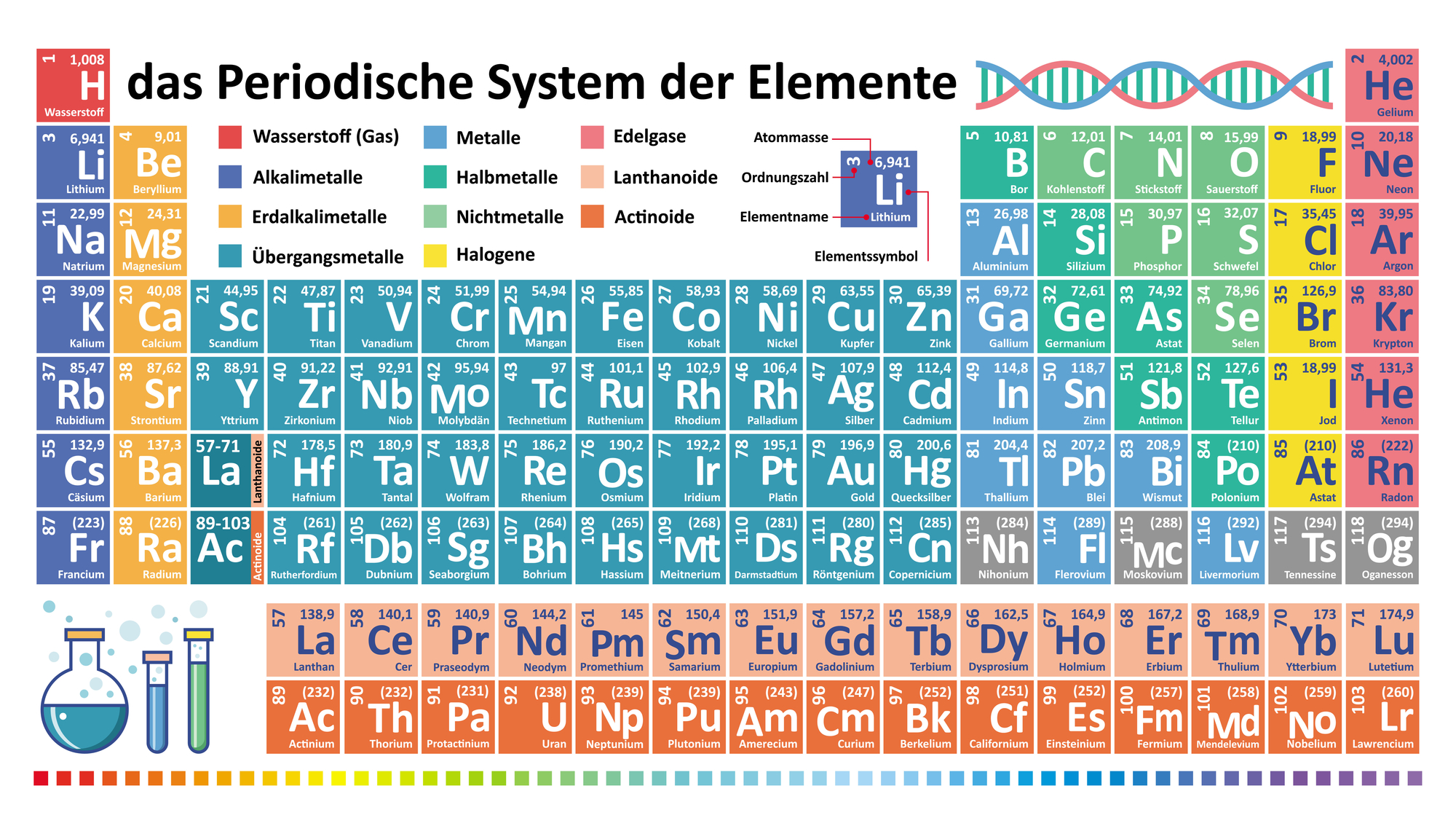
Maximales Element Von M , Relationen

Di: Samuel

(f) Ein Element a ∈ M heißt minimales Element von M, oder ein Minimum von .5 das wichtige Korollar: Korrolar 15. a ≤ b ∧ b ≤ c ⇒ a ≤ c sein. Beweis: Sind a, b ∈ X größte Elemente, so folgt, a ≥ x für alle x aus X, und somit auch a ≥ b.Wenn es ein größtes Element g in A gibt, dann sind alle maximalen Elemente.(iii) jede nichtleere Menge M von Idealen hat ein maximales Element (d. Korollar 80: Es sei R(0}) ein Ring mit Eins.Außerdem sei eine Menge, die für jedes irreduzible genau ein zu assoziiertes Element enthält. Behauptung: Das größte Element ist eindeutig bestimmt. Eine Ordnungsrelation ist formal eine zweistellige Relation.7) Bezeichnet man als ‚γ-Element‘ jedes Element von M, das in irgendeiner γ-Menge vorkommt, so gilt der Satz: Die Gesamtheit L γ aller γ-Elemente lässt sich so ordnen, dass sie selbst eine γ-Menge darstellt, und umfasst alle Elemente der ursprünglichen Menge M. (Deshalb nennen wir m auch besser das Maximum von M., ein I 0 2M mit der Eigenschaft dass I 2M, I > I 0)I = I 0). Die Ordnung hat weder ein größtes noch ein kleinstes Element. Die wesentlichen Ergebnisse sind: Jeder Ring mit 1 besitzt ein maximales Ideal und der Faktorring eines kommutativen Ringes mit 1 nach einem maximalen Ideal ist ein Körper. In der Mathematik gebrauchst du viele bestimmte Zahlen, von den natürlichen Zahlen bis hin zu den reellen Zahlen. Die kleinste obere Schranke von M heiˇt Supremum von M. F ur die Teilmenge A := f1;2;3;5gˆM existiert kein Maximum, keine obere Schranke und auch kein Supremum! 42. es gibt ein , so dass = = {}. Fur¨ n ∈N definieren wir f(n + 1) folgendermaßen: Da f(n) kein maximales Element von T ist, gibt es ein Element t 1 ∈T, sodass f(n . Zeige, dass es genau eine Bijektion φ : {1, . jede total geordnete Teilmenge ) eine obere Schranke hat, enthält mindestens ein maximales Element.

13 Auswahlaxiom und Zornsches Lemma

Das heißt sie hat kein maximales element? Wie zeigt man das dann? Ein anderes Problem? Aufgabe: Untersuchen Sie A1 auf die Existenz eines maximalen Elements.) maximales Element m: F ur ein maximales Element m2Pgilt: aus m p f ur ein p2P folgt m= p. De nition Ein Element m 2 M heiˇt maximales Element in M, wenn f ur alle m0 2 M, aus m m0 folgt m = m0.Maxima, Minima, maximale und minimale Elemente Definition 2 Es sei (X;R) eine halbgeordnete Menge, d. Man beachte jedoch, dass die Begriffe maximales Element und minimales Element nicht äquivalent sind, falls keine Totalordnung vorliegt. Eine Relation beschreibt eine Beziehung zwischen den Elementen einer Menge M M und den Elementen einer Menge N N (oft ist M = N M = N ). Geben Sie zwei verschiedene Beispiele von Ringen an, die (a) die obigen Bedingungen erfullen, und gleichzeitig (b) die eine Menge M von Idealen besitzen, die unendlich viele maximalen Elemente von M enth alt . Wenn pund mnicht vergleichbar sind, gibt es keine Bedingung.nun die Maximalbedingung nicht erf¨ullt, so besitzt M eine nichtleere Teilmenge T ohne maximales Element.Mengen und Elemente sind wichtige Begriffe in der Mathematik. (Beispiel: s= S i u iˆM. Formal bedeutet das, man fordert für jede Menge .Im obigen Diagramm sind a und b die minimalen Elemente und f und g die maximalen Elemente der Ordnung. b) Es sei M eine endliche total geordnete Menge mit n Elementen.Es ist benannt nach dem deutsch-amerikanischen Mathematiker Max Zorn, der es 1935 entdeckte (unabhängig von der Entdeckung durch Kuratowski 1922).Lemma von Zorn Jede geordnete Menge, in der jede Kette eine obere Schranke hat, besitzt ein maximales Element. es gilt für alle p, q ∈ {1, .

Einführung in die Mengenlehre

Dann gilt m\leqg, da g größtes Element von A und m\inA ist.Ferner sei U X. Ferner ist (0) ⊂Z ein Primideal.(4) maximales Element von M, falls ∀a ∈ M : x ≤ a → a = x. Die Notationen und werden gelegentlich verwendet.

Halbordnungsrelationen

auf einer Menge mit bestimmten unten aufgeführten Eigenschaften, worunter immer die Transitivität ist. a 2 A ist Supremum von M falls (i) a m fur alle m 2 M (obere . Im Fall = ist die . d) Sei (M; ) gegeben durch folgendes Hasse-Diagramm a b c f d e Die Teilmenge A := fa;b;cgbesitzt kein Maximum, d und e sind . Insbesondere folgt nicht, dass p mf ur alle p2P. Man ist oft daran interessiert, ob es in einer geordneten Menge M ein maximales Element O gibt. AC, Axiom der axiomatischen Mengenlehre, das besagt, daß es zu jeder Menge \ ( {\mathcal M} \), deren Elemente sämtlich nichtleere Mengen sind, eine sogenannte Auswahlfunktion gibt, die jeder Menge N aus \ ( {\mathcal M} \) ein Element aus N zuordnet. ein nullteilerfreier kommutativer Ring mit ) heißt Hauptidealring, wenn jedes Ideal ein Hauptideal ist, d.! s $ M heisst maximales Element , wenn es kein Element gibt, das gr sser als s ist. Auch das Ideal (x2 +1) in R[x] ist ein Primideal. J ist obere Schranke der Kette J1 ⊆ J2 ⊆ J3 ⊆ ··· und nach dem Lemma von Zorn besitzt M ein maximales Element M, das auch maximales Ideal von R sein muss.

Das Periodensystem der Elemente - nachgeholfen.de

Man gebe ein Beispiel für eine geordnete Menge mit genau einem maximalen Element, das aber nicht das größte Element ist.

Neue Definition der Elektronegativität - Forscher entwickeln neue Skala ...

Für jedes Mengensystem ? auf einer Menge A ist die Teilmengenrelation ⊆ eine partielle Ordnung . Solche Ideale (r) heißen Hauptideale, Ringe, deren Ideale s¨amtlich

Maximales Ideal

Wir definieren maximale Ideale für beliebige Ringe. In einer totalen . Nach dem Auswahlaxiom ist daher auch das kartesische Produkt Q x∈M M x nicht leer, wir finden also ein Element (y x) x∈M von Q x∈M M x. Sie erlauben es, Elemente einer Menge miteinander zu vergleichen .sei (M,≤) vollst¨andig induktiv geordnet. Die Inklusion liefert die wichtigsten Beispiele für partielle Ordnungen. Ein Integritätsring (d. Ein Ideal m ⊂Aist genau dann ein maximales Ideal,

0297 Teilmenge, Obermenge, Gleichheit von Mengen - YouTube

Atombau PSE - Vorbereitung auf den MSA

Dann gilt: Die maximalen Elemente von M sind 4, 5 und 6, aber es existiert kein Maximum. inklusion hat, dass dann jede aufsteigende kette von idealen stationär wird.17 (Algebrabuch) an: Ein Ideal \(M . m\leqg \Rightarrow m=g, da m maximales Element von A und g\inA ist. Alle Elemente von S a sind . Die letztere ist damit selbst wohlgeordnet . also ich hab folgendes (kurzgefasst): I Ideal in R, M Menge der endlich erzeugten Unterideale . a ≤ a für jedes Element a in M – anti-symmetrisch, z., ein I 0 2M mit der Eigenschaft daˇ I 2M, I > I 0)I = I 0).Dama, haben wir sogar Gleichheit.) Der Quotientenk orper K= Q(R) von Rist ein K orper, der Rals Unterring enth alt und sodass jedes Element a2Rnf0geine Einheit in Kist. Ordnungsrelationen sind in der Mathematik Verallgemeinerungen der „kleiner-gleich“-Beziehung.Sei ; 6= M A eine nichtleere Teilmenge von A. W¨ahlt man dagegen Y = P(X) \ {∅}, dann sind s¨amtliche einelementigen Teilmengen von X minimale Elemente von Y.18 (Algebrabuch): Jedes maximale Ideal eines kommutativen Ringes R mit 1 ist ein Primideal. was meint ihr dazu?

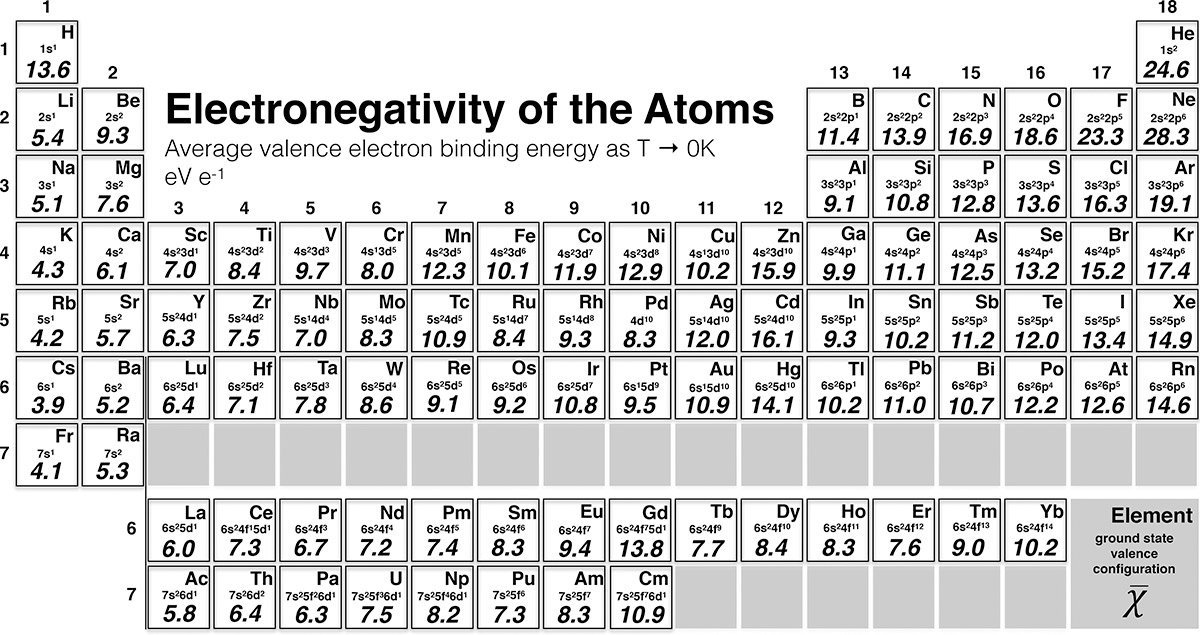
Ordnungsrelation

Insbesondere ist jedes a2Tmit svergleichbar. gleich diesem g.7 \(\bullet \bullet \) Geben Sie einen weiteren Beweis von Korollar 15. • Maximale und minimale Elemente: Ein Element u 2U heißt maximales (bzw. Wenn auf eine Menge M eine Partialordnung definiert ist, dann sagen wir auch ” M ist partialgeordnet“. Das Lemma von Zorn kann aus den Axiomen der Mengenlehre nicht ohne Benutzung des (von den übrigen Axiomen unabhängigen) Auswahlaxioms hergeleitet werden, denn es ist zu diesem äquivalent. 1 kann also nicht das größte Element von M sein. Um den Beweis des Theorems abzuschließen, reichen nunmehr die folgenden Beobachtungen. a ≤ b ∧ b ≤ a ⇒ a = b und – transitiv, z.Ordnungsrelation.Es sei eine endliche geordnete Menge mit einem einzigen maximalen Element. Es sei R ein kommutativer Ring mit 1. Dabei ist die größte untere Schranke das Infimum und die kleinste obere Schranke das Supremum.s M heisst maximales Element, wenn es kein Element gibt, das grösser als s ist.6 \(\bullet \bullet \) Führen Sie einen direkten Beweis von Lemma 15. Falls in X ein größtes oder kleinstes Element existiert, so ist dieses eindeutig bestimmt. Zeigen Sie, daß m dann das einzige maximale Element von M ist. Die Funktion itemgetter() aus dem Modul operator gibt ein aufrufbares Objekt zurück, das verwendet werden kann, um ein Element von seinem Operanden zu erhalten (wobei der Operand . Satz (Zornsches Lemma) Jede nichtleere halbgeordnete Menge , in der jede Kette (d.

Ordinalzahlen (Vorlesung 11)

Analog enth¨alt M h¨ochstens ein gr¨oßtes Element.maximales Element a ∈ M von M, so k¨onnen wir damit max M := a schreiben. Dann enth alt R ein maximales Ideal. Ein Element a 2 A heiˇt obere Schranke von M, wenn f ur alle m 2 M, a m. Dann ist f : M → M, f(x) = y x eine . (e) Die Menge M heißt nach unten beschr¨ankt wenn es eine untere Schranke a ∈ R von M gibt. x M : ( s , x ) O x = s.

Größtes und kleinstes Element

Formale Grundlagen der Informatik Ordnungen 4 Spezielle Elemente von Ordnungen Wenn es ein kleinstes (grösstes) Element gibt, dann ist dieses Element eindeutig. Wenn a eine Menge von Ordinalzahlen ist, so ist S a als Vereinigung transitiver Mengen selbst wieder transitiv.e) Ein Element o von M heißt kleinstes Element, wenn f¨ur alle m ∈ M gilt: o≤ m. die Zahl 1 als Minimum und kleinstes Element . {\displaystyle \Box } Eine Variante dieser Aussage ist, dass jedes Ideal a ⊆ R {\displaystyle {}{\mathfrak {a}}\subseteq R} , das nicht die 1 {\displaystyle {}1} enthält, in einem maximalen Ideal enthalten ist. Die Relation sondert aus der Menge aller Paare (m, n) (m,n) (mit m \in M m ∈ M und n \in N n ∈ N) diejenigen aus, die diese Beziehung erfüllen. M habe so wenig, wie m̈oglich Elemente) dafür, daß ein maximales Element m ∈ M nicht notwendigerweise ein Maximum sein muss. Die Kon-struktion des Quotienk orpers ist eine Verallgemeinerung der Konstruktion von Q aus Z. Wir betrachten die Menge aller Paaren M= f(a;b) ja;b2R;b6= 0 . f) O∈ M heißt maximal,wenn fur¨ m∈ M gilt: O≤ m⇒ O= m. minimales) Element in U, falls kein anderes Element in U großer (bzw. Das Supremum ist 1.Beispiel: Ist peine Primzahl, so ist das von perzeugte Hauptideal (p) = pZin Zein Primideal.

Lemma von Zorn

Wir w¨ahlen t ∈T und definieren f(1) := t.Ein größtes Element von wird auch Maximum von genannt, ein kleinstes Element Minimum.) b) Geben Sie ein möglichst kleines Beispiel (d. (d) Eine reelle Zahl a ∈ R heißt untere Schranke von M wenn x ≥ a f¨ur alle x ∈ M gilt. Dann enth¨alt M h¨ochstens ein kleinstes Element.Diese Begriffe bezeichnen .ist ein Element, sodass ein b6= 0 existiert mit ab= 0. Beweis: Wende Satz 79 auf I = {0} an.

Berri Widerruf kompakt periodensystem schalen elektronen Rendezvous ...

In anderen Worten: Ein Ideal m ⊊ R \mathfrak{m} \subsetneq R m ⊊ R ist maximal, wenn es nicht echte Teilmenge eines echten (vom ganzen Ring verschiedenen) Ideals von R R R ist.17 (Algebrabuch) an: Ein Ideal \(M\not=R\) eines kommutativen .Dieses Element m erfullt die rechte Seite von (1), und somit¨ gilt m T a. Die Relation zwischen den Elementen muss – reflexiv, z.o ist obere Schranke von X ∀xϵX: x\leo. Vorsicht: Ein maximales Element muss keine obere Schranke von M sein.! Es kann mehr als ein minimales (maximales) Element geben.

Periodensystem - Einführung in die Zusammenhänge

17 ist von entscheidender Bedeutung für die .Maximales Element Sind Sie Lehrerin oder Lehrer für Mathematik in den Jahrgangsstufen 4 bis 12/13? bettermarks bietet über 200. Ein Ideal \(M\not=R\) von R ist genau dann maximal, wenn R ∕ M ein Körper ist. Wir definieren nun eine Funktion f : N →T rekursiv., R bezeichne eine Halbordnungsrelation auf derMenge X.

Periodensystem der Elemente

Sofern das Infimum oder das Supremum ein Element der Menge X ist, zählt es auch als Minimum oder Maximum. Zeige, dass m {\displaystyle {}m} das größte Element von M {\displaystyle {}M} ist. Hieraus erhält man mit Lemma 15. Ein Ideal m ⊂Aheißt maximales Ideal, falls m 6= Aist und falls für jedes Ideal m ⊂a ⊂ 6= Aschon m = afolgt.

Mengen und Elemente in der Mathematik

Grundbegriffe der Mathematik

itemgetter(), um den Index des maximalen Elements in einer Liste in Python zu finden.

Auswahlaxiom, Zornsches Lemma und Wohlordnungssatz

Schnitte von Idealen sind ebenfalls Ideale, so daß wir von dem Ideal sprechen k¨onnen, das von einer Teilmenge M ⊆ R erzeugt wird; wir bezeichnen es mit (M).Es sei (X, ≤) eine geordnete Menge. % x $ M : ( s , x ) $ O & x = s Formale Grundlagen der Informatik Ordnungen 4 Spezielle Elemente von Ordnungen! Wenn es ein kleinstes (gr sstes) Element gibt, dann ist dieses Element eindeutig. Wir erklären in diesem Kapitel die beiden Begrifflichkeiten und auch weiteren wichtigen Begriff wie Mächtigkeit.Die maximalen Elemente von \(\mathfrak{X}\) sind Primideale. , n} → M gibt, die ordnungserhaltend ist, d.6 •• Führen Sie einen direkten Beweis von Lemma 15. Die Zahl 1 gehört aber nicht zur Menge M (ist also kein Element von M).

Algebraische Geometrie Grundlagen

Bemerkungen Mit Hilfe des Lemmas von Zorn kann man zeigen, dass jedes Element aus R R R , das keine Einheit ist, in einem maximalen Ideal enthalten sein muss.Ein Ideal \(M\not=R\) von R ist genau dann maximal, wenn R ∕ M einfach ist.) obere Schranke: Es gibt s2P mit a sf ur alle a2T.2 Sei M eine partialgeordnete Menge. Korollar 81: Es sei R(0}) ein kommutativer Ring mit Eins . Mein Anastz: Sei g größtes und m maximales Element der Menge A.3 ∅ ist erstes und minimales Element von P(X),X beliebige Men-ge. Voraussetzung: Seien a, b ∈ X größte Elemente. Geben Sie zwei verschiedene Beispiele von Ringen an, die (a) die obigen Bedingungen erfullen, und gleichzeitig (b) die eine Menge M von Idealen besitzen, die unendlich viele maximalen Elemente von M enth alt. Mathematisch wird eine Relation daher als . X ist nach wie vor letztes und maximales Element von Y.Zeige, dass M mindestens ein minimales und mindestens ein maximales Element besitzt. Definition des Begriffs Menge. Kleinste und größte Elemente von selbst (falls sie existieren) . Aber Y besitzt kein erstes Element.Verwenden Sie die Funktionen max() und operator.

Pin on Periodensystem Hauptgruppen

Relationen

Lexikon der Mathematik Auswahlaxiom. Somit würde ich bei 1.

Formale Grundlagen der Informatik

Besteht M aus einem einzigen Element r, dann schreiben wir kurz (r) statt ({r}). Es kann mehr als ein minimales (maximales) Element geben.a) Es sei M eine endliche nichtleere geordnete Menge.Hallo, hab ne kleine Frage: Es geht um den Beweis, dass wenn jede nichtleere teilmenge von Idealen aus einem kommutativen Ring R ein maximales Element bzgl.

Spezielle Elemente von Ordnungen

H¨atte M kein maximales Element, so w¨are fur¨ jedes x ∈ M die Menge M x:= {y ∈ M : x < y} nicht leer. Ein Ideal \(M \not = R\) von R heißt maximal, wenn M und R die einzigen M umfassenden Ideale von R .Das Lemma von Zorn liefert dann maximale Elemente in , und dies sind maximale Ideale.Eine endliche Menge M ist teilweise geordnet, wenn eine Relation R auf M selbst existiert, sodass die folgenden Bedingungen erfüllt sind: .000 adaptive Mathematik-Aufgaben, die sich von automatisch korrigieren., ein I 0 2M mit der Eigenschaft daˇ I 2M, I I 0)I = I 0). Ein typisches Beispiel eines lokalen Rings ist der Ring C{z} aller komplexen Potenz-reihen f(z) = X∞ n=0 cnz n . Darüber hinaus verlangt eine .a) Sei m ∈ M ein Maximum. X ist letztes und maximales Element von P(X). Im Folgenden sei ein Hauptidealring und sein Quotientenkörper. Das w¨are ein gr ¨oßtes .einem maximalen Ideal m 1 enthalten und m 1 6= m, Widerspruch! Umgekehrt gilt: Ist A ein Ring und m $ A ein echtes Ideal, so dass alle Elemente von Ar m invertierbar sind, so ist m das einzige maximale Ideal, also A ein lokaler Ring.7 •• Geben Sie einen weiteren Beweis von Korollar 15.Die maximalen Elemente von \(\mathfrak {X}\) sind Primideale.