Massenträgheitsmoment Steiner _ Flächenträgheitsmoment
Di: Samuel
Ferienkurs Gramos Qerimi, Jakob Unfried Stand: 27. Die Berechnung eines beliebigen Trägheitsmomentes kann mit Hilfe des Steiner’schen Satzes auf die Berechnung des Trägheitsmomentes bezüglich einer Achse durch den .6 Der Satz von Steiner für Trägheitsmomente Bisher wurden die Massenträgheitsmomente auf eine durch den Körperschwerpunkt S verlaufende Achse bezogen. Du könntest eventuell sagen: Die Hanteln haben das Trägheitsmoment J=0, wenn sie in der Mitte liegen. Dabei gibt den Abstand des Schwerpunkts von der parallel verschobenen Drehachse an. Der Satz von Steiner. Wenn man das Trägheitsmoment eines Körpers in Bezug auf eine durch seinen Schwerpunkt gehende Achse kennt, liefert der Steinersche Satz das Trägheitsmoment in Bezug auf eine andere dazu parallele Achse .
Theoretische Physik: Mechanik
J S sei das Trägheitsmoment durch den Schwerpunkt, parallel zur Rotationsachse, m sei die Masse des Körpers und r a der Abstand der Drehachse vom Schwerpunkt.

Das Trägheitsmoment, auch Massenträgheitsmoment oder Inertialmoment, gibt die Trägheit eines starren Körpers gegenüber einer Änderung seiner Winkelgeschwindigkeit bei der Drehung um eine gegebene Achse an ( Drehmoment geteilt durch Winkelbeschleunigung ). Verifizieren Sie den Satz von Steiner: , wobei der Abstand der Achsen und die Masse des Würfels ist. Da ich jedoch um eine andere Achse drehen möchte (hier um die X-Achse (siehe Koordinatensystem am linken Träger)) habe ich zu dem M2 einfach den . Dabei ist J A das Trägheitsmoment des Objekts (in diesem Fall einer Kugel) um den eigenen Schwerpunkt, m die Masse des Objekts und l der Abstand des Schwerpunkts von der Drehachse.Massenträgheitsmoment von der Aluminiumstange Der Zylinder rotiert in diesem Experiment um seine eigene Schwerpunktsachse, so muss man nicht Gebrauch machen von dem Satz des Steiner.

In rotierenden Systemen steckt Rotationsenergie.
Massenträgheitsmoment Ausarbeitung PDF Neu
Trägheitsmoment Technische Mechanik: Bedeutung der richtigen Einheit .Der Steinersche Satz (auch Satz von Steiner, Steiner-Regel oder Parallelachsen-Theorem) geht auf Untersuchungen von Jakob Steiner zurück und dient der Berechnung des Trägheitsmomentes eines starren Körpers für parallel verschobene Drehachsen. Das Trägheitsmoment ist somit vergleichbar mit . Für ein Vielteilchensystem (z.Huygens−Steiner Gleichungen (Wechsel des Bezugspunktes, Schwerpunkt C) −?P=?C+m[b2+c2 −ab −ac ab c 2+a −bc −ac −bc a2+b2] Trägheitsmoment bezüglich einer Achse ? (‖?‖=1) Ie=∫ r2 dm K =?⋅?⋅? Trägheitsradius k: IH=[Ixx H 0 0 0 IyyH 0 0 IzzH] Ie=! k2m⇒ k=√ Ie m.Wir berechnen zunächst den Schwerpunkt.Mathefix hat Folgendes geschrieben: Wenn die Drehachse nicht durch Massenschwerpunkt verläuft, muss der Satz von Steiner angewendet werden: = Massenträgheitsmoment bezogen auf den Schwerpunkt.
M16 Massenträgheitsmoment
In diesem Video erklären wir dir alles über den Satz von Steiner aus dem Bereich Maschinenbau.
Trägheitsmoment
Rotationsenergie.
![[View 21 ] Mathematisches Pendel Skizze](https://www.ingenieurkurse.de/assets/courses/media/physikalisches-pendelneu-ca.png)
Dann verschiebst du die 2 Hanteln um 0,6 m nach außen und kommst mit dem Satz von Steiner auf J= (0+2*2*0,6²) kgm².1 MTM bei parallel verschobenen Drehachsen – Satz von Steiner Ein Körper habe bei Rotation um eine Achse S durch seinen Schwerpunkt das bekannte Massenträgheitsmoment (MTM) J S. Wir brauchen nur noch die z-Koordinate des Schwerpunktes: Für die Fläche 1 (mittlerer Steg) gilt dabei: z1 = 0. = Abstand Massenschwerpunkt von der Drehachse. Das folgt daraus, dass der Steinersche Anteil stets positiv ist, wenn man eine Verschiebung vom Schwerpunkt weg durchführt. Aus Symmetriegründen erkennbar: ySliegt im Urpsrung.Viele weitere Videos für’s Studium gibt’s auf https://studyflix.Themengebiet════════════Es wird das Massenträgheitsmoment eines dünnen Stabes berechnet. Der Steiner’sche Satz (nach dem Schweizer Mathematiker Jakob Steiner, 1796-1863) besagt: Das Trägheitsmoment eines starren Körpers mit der Masse M M um eine beliebige Drehachse im Abstand l l von seinem Schwerpunkt ist gleich dem Trägheitsmoment um die parallele Drehachse, die durch den Schwerpunkt verläuft, .Das Eigenträgheitsmoment I ξξ ist immer kleiner, als das Trägheitsmoment I yy, welches auf eine beliebige parallele Schwerachse bezogen ist.Sondern alle Angaben beziehen sich auf die Drehachse. Das Trägheitsmoment (auch Massenträgheitsmoment genannt) ist eine Größe, die angibt, welches Drehmoment benötigt wird, um bei der Rotation eines starren Körpers eine Änderung der Winkelgeschwindigkeit hervorzurufen.de/In diesem Lernvideo zu Flächenträgheitsmomenten aus dem Fach Mechanik 2 stellen. Speziell für den Fall eines um seine Symmetrieachse rotierenden Zylinders konstanter Dichte (Abb.Trägheitsmoment. Anmeldungsdatum: 29. Bezeichnet Js das Trägheitsmoment bezüglich einer Achse durch den Schwerpunkt und JA das bezüglich einer dazu parallelen Achse im Abstand a (siehe Abb. Die beiden oberen Objekte haben eine Höhe von 97,5 mm und das untere Objekt eine Höhe von 20 mm.Trägheitsmoment, , für einen Massenpunkt mit Abstandsvektor r vom Rotationszentrum über die Gleichung.In der Praxis ist es oft üblich, das Trägheitsmoment nicht zu berechnen, sondern mit relativ hoher Genauigkeit experimentell zu bestimmen.
), so sagt der Satz von Steiner aus: mit m als der . Der Satz von Steiner lautet wie folgt: J 1 – Trägheitsmoment des Körpers auf Drehachse 1 (= Schwerachse = Achse, auf der sich der Schwerpunkt des . Folglich liegt der Schwerpunkt in der Mitte des Stabes und die Massendichte ist konstant. a) Durchstosspunkt liegt nicht auf der Achse durch den . Hier geht’s zur Tabelle der Flächenschwerpunkte (Schwerpunkte), die für den Steiner Anteil relevant sind.
Trägheitsmoment
Schwerpunktpositionen in Abhängigkeit von z der Flächen 2 und 3 lassen sich leicht berechnen: Beispiel: Setzen wir z1 , z 2 und z3 in .Technische Mechanik IV Arbeitsblatt – Kinematik Universität Siegen FB10 – Lehrstuhl für Baustatik 1 Massenträgheitsmomente bestimmter Körper
Trägheitsmomente
In der technischen Mechanik wird das Trägheitsmoment verwendet, um verschiedene Probleme zu lösen, die mit dem Drehverhalten von Körpern verbunden sind. Bezugsachse ist die Schwereachse senkrecht z.Flächenträgheitsmoment Achteck (Oktagon) Iy = Iz = 1 + 2 2–√ 6 b4 ≈ 0, 638b4. Die Rotationsachse bzw.Lösung: Nach Satz von Steiner berechnet sich das Trägheitsmoment J um eine Rotationsachse wie folgt.2017 Seite 2 1 Trägheitsmoment & Satz von Steiner .Der Steiner’sche Satz. Man kann den Steinerschen Satz für zwei beliebige parallele Drehachsen verallgemeinern. In der Praxis bedient man sich hierzu einer speziellen Tabellenkalkulation . Von der Berechnung der Belastung eines rotierenden Bauteils bis hin zur Festlegung der Spezifikationen für einen .15 Satz von Steiner # Es gilt \(\Theta_1 = \frac{m}{12} l^2\) Daraus kann nach dem folgenden Satz von Steiner das Trägheitsmoment bezüglich einer zur Schwerpunktsachse parallel verlaufenden Achse bestimmt werden . Mechanik Maschinendynamik Prof.-muss in einem solchen Fall zu dem zentrischen Massenträgheitsmoment lediglich der Steiner-Anteil addiert werden, und der hat die Größe Masse x Abstand². Damit spielt es die gleiche Rolle wie die Masse im . Definition Hauptträgheitsmoment Wird nun ein unregelmäßig geformter Körper betrachtet, um eine Achse rotiert, so verändert sich dessen Trägheitsmoment in Abhängigkeit von der Lage dieser Achse.
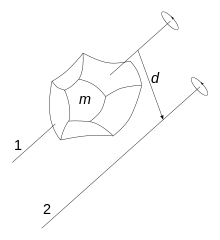
Das gesuchte Trägheitsmoment J A kann als Summe zweier Trägheits-momente dargestellt werden. Dieser Satz heißt im Deutschen, nach dem Schweizer Mathe-matiker Jakob Steiner, der Satz von Steiner, in der englisch-sprachigen Literatur findet man ihn unter der Bezeichnung Parallel-Axis Theorem. Bei Rotation um eine zu S parallele Achse A, die von S den Abstand a hat, gilt: SA Die Schwierigkeit bei der Anwendung des Satzes von Steiner besteht allerdings zumeist darin, den Abstand a zu ermitteln. Für die Rotationsenergie gilt E R o t = 1 2 ⋅ J ⋅ ω 2 wobei J das Trägheitsmoment ist. Rotiert ein Körper mit einer Masse um eine Achse, die im Abstand parallel zum Schwerpunkt verläuft, so muss zum jeweiligen Wert des Trägheitsmoments noch der Term hinzu addiert werden. 3-Euro-Spende über PayPal: https://ww.ch/skripteNiveau der videos: * Einfach, ** Berufsschule / Gymnasium, *** Uni / FH Das Trägheitsmoment ist nicht alleinige Eigenschaft eines Körpers, sondern abhängig von . Dafür wird der Steineranteil zu- sätzlich zu dem Massenträgheitsmoment der Metallscheibe addiert.0:00 Beispiele0:50 Massenträgheitsmoment, Trägheitsmoment1:30 Trägheit4:50 Tabelle mit den Trägheitsmomenten5:59 Eier, roh und gekocht6:40 Hochseil-Artist7:4.Na, aus dem oben gesagten sollte es jetzt nicht mehr schwer sein, das gesuchte Massenträgheitsmoment des mondförmigen Teils bezüglich O zu errechnen.In diesem Video erklärt Dan, was es mit dem Satz von Steiner auf sich hat, den wir bei der Berechnung von Flächenträgheitsmomenten dann brauchen, wenn wir da. definierte Größe. Das Trägheitsmoment bei Parallelverschiebung der Rotationsachse .Das Massenträgheitsmoment hängt von der Lage der Drehachse ab. Jetzt weiter lernen!
Massenträgheitsmomente
J A =J S +mr2a (7) Aus dem Satz von Steiner folgt, dass ein minimales . Bezugsachse verläuft senkrecht zur Stabachse.Also mein Massenträgheitsmoment, bezogen auf den Schwerpunkt mit Rotation um die Z-Achse (siehe Koordinatensystenm unten rechts), müsste unter Prinzipal Moments/G mit M2 angezeigt werden. Was kriegst du raus? h) Und aus dem kannst du wieder leicht das Massenträgheitsmoment des mondförmigen Teils bezüglich S errechnen.
Satz von Steiner
Ist das Trägheitsmoment für eine Achse durch den Schwerpunkt eines Körpers bekannt, so ist das Trägheitsmoment für eine beliebige parallel verschobene Drehachse .
Das Trägheitsmoment: Spezial- und Sonderfälle berechnen
Massenträgheitsmoment eines homogenen Rotationsk örpers
![Satz von Steiner · bei Flächen und Massen · [mit Video]](https://d1g9li960vagp7.cloudfront.net/wp-content/uploads/2018/12/TTTräger_SEO-1024x576.jpg)
Das lässt sich dadurch erklären, dass in diesem Fall der Schwerpunkt des Körpers auf einer Kreisbahn .Satz von Steiner. Damit kann die Rotationsenergie ausgedrückt werden als. Um nun hier das Massen- trägheitsmoment zu berechnen können wir Gebrauch machen von den uns hergelei- teten Formel (5)
Satz von Steiner, Aufgabe: Hantel
2 Trägheitsmoment einfacher starrer Körper. Iyz = Iyz1 = 0. Das Trägheitsmoment J hängt vom Körper und seiner Rotationsachse ab. Ein sehr dünner Stab der Länge habe die Masse , die homogen über den Stab verteilt sei. Der Abstand zwischen den beiden Achsen sei : (237) Wie man leicht nachrechnen kann, ergibt sich damit für . Das Massenträgheitsmoment bezüglich A ist ??=∑ I?·?? 2 .Das Trägheitsmoment . Ein vollständiges Rechenbeispiel mit ausführlichem Lösungsweg ist hier zu finden . (i) Trägheitsmoment eines dünnen Stabes. Iy1 = Iz1 = 1 + 2 2–√ 6 b4 ≈ 0, 638b4.dem Trägheitsmoment bezüglich einer beliebigen anderen, zur ersten parallelen Achse verknüpft.Wie funktioniert der Satz von Steiner in der Mechanik? Hier wird es am Beispiel einer unsymmetrischen Hantel erklärt.Skripte: http://www. Das Trägheitsmoment wird in der Physik zumeist mit dem Symbol J gekennzeichnet.
Massenträgheitsmoment (Autodesk/Inventor)
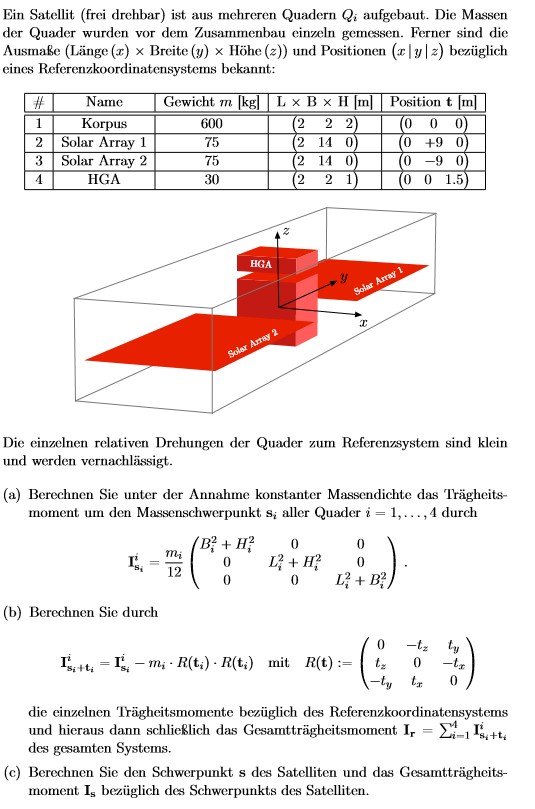
Das Trägheitsmoment eines Körpers ist dann am geringsten, wenn die Drehachse durch den Schwerpunkt geht.Massenträgheitsmoment theoretisch bestimmen.
Flächenträgheitsmoment
-ergibt sich das zentrische Massenträgheitsmoment für beliebige Raumrichtungen aus dem Trägheitsellipsoid, dessen Achsen die Hauptträgheitmomente sind, und dessen . Institut für Technische und Num.3 Der Satz von Steiner Nach Betrachtung von Rotationsachsen durch den Schwerpunkt eines Körpers wird nun der Koordina-tenursprung in den Schwerpunkt S des Körpers mit der Masse I gelegt und dessen Rotation um die Achse A, die nicht durch S geht, untersucht (Bild 3). Das Wichtigste auf einen Blick. J = J A +ml2 J = J A + m l 2.Trägheitsmoment bei zueinander parallelen Achsen – Satz von Steiner. bezeichnet man als Massenträgheitsmoment eines Körpers bezüglich seiner Rotationsachse A.Das Trägheitsmoment berechnen. Für einen einzigen definierten Massenpunkt lässt sich das Massenträgheitsmoment mithilfe folgender Formel recht einfach berechnen: m – Masse [kg] r – Abstände von der Drehachse [m] Der Abstand des Massenpunktes hängt dabei . starrer Körper) geht diese Gleichung bezüglich einer vorgegebenen Drehachse in die Summe der mit dem Quadrat.Trägheitsmoment – Definition und Erklärung.

Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Beispiel: Flächenträgheitsmomente Dreieck wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt.Das Trägheitsmoment einer hierzu parallelen Achse kann man – wie schon geschrieben – mit Hilfe des Satzes von Steiner berechnen.
Rotation, Trägheitsmoment und Steiner
Hierbei wird die dynamische Winkelrichtgröße verwendet. Beispiel: langer Stab# Fig. Zusätzlich wird mit Hilfe des Satzes von Steiner das Massenträgheitsmoment berechnet. Anderenfalls geht man folgendermaßen vor: 2 ( )2 2 2 b s bs a bs as s a as mr m r r mr Θ=Θ+ =Θ+ − Θ=Θ− Beispiele: (In der Vorlesung wurden der Quader, der Kreisringzylinder, der schlanke Stab, die dünne Kreisscheibe und die . 4) ergibt sich: JmR=⋅⋅05, 2 (4) Rotiert ein Körper um eine um a gegen den Schwerpunkt verschobene (exzentrische) Achse, so verknüpft der Satz von Steiner dieAus diesen gemessenen Periodendauern wird das Massenträgheitsmoment der Metallscheibe ermittelt.AW: Massenträgheitsmoment, Massenschwerpunkt, Satz von Steiner Bei der Abmessung in z Richtung ist mir ein Fehler unterlaufen.Satz von Steiner, beschreibt den Zusammenhang von Trägheitsmomenten bezüglich Achsen, die nicht durch den Schwerpunkt gehen.Der Satz von Steiner darf nur angewendet werden, wenn eine der beiden Achsen durch den Massenmittelpunkt verläuft.Alle Videos und Kurse von BrainFAQ findest Du unter: https://www. Dies ist bei bekanntem Hauptträgheitsmoment relativ einfach.Berechnen Sie für einen Würfel mit Kantenlänge das Trägheitsmoment bezüglich einer Kante und das Trägheitsmoment bezüglich einer dazu parallelen Achse durch den Schwerpunkt. Die Drehache ist senkrecht zum Stab gewählt. ihres jeweiligen senkrechten Abstands zur Drehachse multiplizierten . Diese Spezialfälle sind dadurch gekennzeichnet, dass jeweils die Drehachse 2 in Bezug auf die durch den Körperschwerpunkt verlaufende Drehachse 1 um einen bestimmten Abstand d verschoben ist.
- Matheaufgaben Zum Üben Pdf , Matheaufgaben online üben interaktive Mathe Aufgaben
- Mary Sue Katzen Test _ Mag Ihre Katze Sie?
- Mathias Wagner Fraktion , Amokfahrt in Berlin
- Matlab Cody Player | how can i build a tic tae toe game in matlab
- Martin Von Bergen Depressiv _ Wie reagieren Männer, wenn Frauen sich zurückziehen?
- Marylandbrücke Anwendungsgebiete
- Matica Technologies Ag – Newsroom
- Mathematica Quick History | $HistoryLength—Wolfram Language Documentation
- Matt And Luciana Damon , Matt Damon’s Kids: Meet His Daughters With Wife Luciana Barroso
- Mathematik Im Kindergarten Bücher
- Masks Meaning _ The Meaning of Masks: Masks As Transformation
- Masterarbeit Wie Lange , Wie lang ist der Methodikteil?