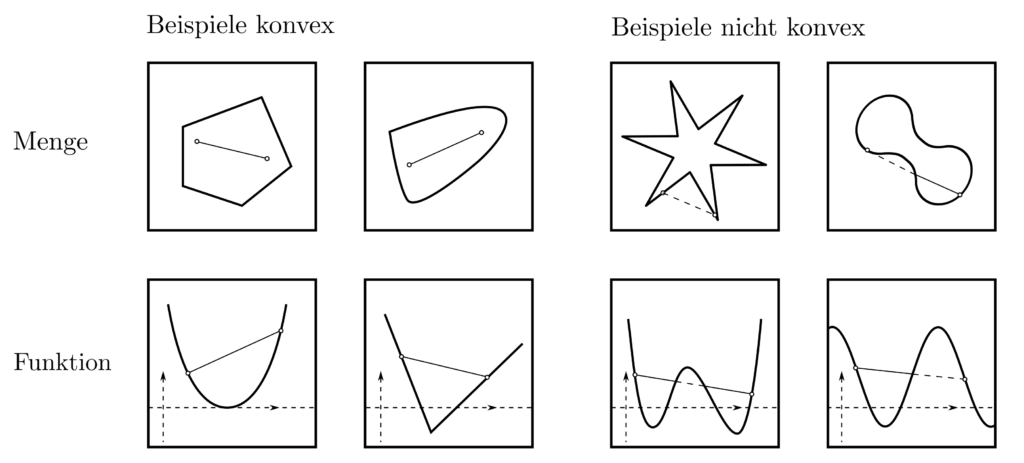
Konvexität Funktion : Konvexe Menge
Di: Samuel
Und wie genau lässt sich der Zusammenhang mit der 2.
Krümmungsverhalten: Erklärung & Bestimmen
Hallo zusammen, ich muss die Konvexität der folgenden Funktion berechnen und weiß nicht weiter: f (x,y) = x³-xy+y³.Funktionen Erst die natürlichen Betrachtungen gemacht, ehe die subtilen kommen, und immer vor allen Dingen erst versucht, ob etwas ganz simpel und natürlich werden könne.Kurvendiskussion.Es gibt diverse nützliche Kriterien zur Feststellung der Konvexität einer Funktion, so gelten folgende Sätze (hier ohne Beweis vorgestellt): Satz 7. Sei also ein Optimierungsproblem der Form
e Funktion • Erklärung, Rechenregeln, Beispiele · [mit Video]
Dann ist f konvex genau dann, wenn f(x+h)·f(x)+Df(x)h für alle x,x+h 2 ⌦.Wir werden in § 5. • Eine nicht-konvexe Funktion, die keine lokalen Minima besitzt, wird als quasikonvex .
Kurvendiskussion einfach & vollständig erklärt • StudyHelp
Stichworte: Großhirnrinde. Kurvendiskussion Grundlagen. Die Grafische Darstellung und allgemeine Definition von konvexen und konkaven Funktionen erklären wir dir ausführlich in diesem Kurstext. Ziel ist es die rechte Seite auf die folgende Form zu bringen um den Vergleich anstellen zu können, ob die obige Funktion größer oder kleiner ist als die folgende Funktion:
Hesse-Matrix
Nach der Betrachtung der konvexen Mengen haben wir uns konvexen Funktionen zuge-wandt. Zuvor wollen wir noch zeigen, daß .Um das Krümmungsverhalten (konvex, konkav) zu entscheiden, reicht es die Definitheit der Hessematrix zu kennen und eine wichtige Voraussetzung zu prüfen. Definitionsbereich : Wertebereich: Symmetrie: ist nicht symmetrisch. Bei ihnen wird lediglich gefordert, dass . Logarithmische Konvexität von Funktionen ist ein Spezialfall der Konvexität von Funktionen und spielt eine Rolle bei der Charakterisierung der Gammafunktion mittels des Eindeutigkeitssatzes von Bohr . Der Text ist unter der Lizenz „Creative-Commons Namensnennung – Weitergabe unter gleichen . konvex; Liveticker Loungeticker. In der Mathematik heißt eine geometrische Figur oder allgemeiner eine Teilmenge eines euklidischen Raums konvex, wenn für je zwei beliebige Punkte, die zur Menge gehören, auch stets deren Verbindungsstrecke ganz in der Menge liegt.
Wendepunkte einer Funktion
Um die Indifferenzkurve zu berechnen, solltest du die Birnenmenge B als Funktion der Apfelmenge A ausdrücken: B ( A) = ( 4 A 1 2) 2. Dann kann man das Vorzeichen der zweiten Ableitung auf den bestimmten Intervallen bestimmen, indem man die Werte der zweiten . Extrempunkte (Hochpunkte & Tiefpunkte) Wendepunkte.Kapitel 3 Konvexe Funktionen Nun betrachten wir Funktionen, die im Zentrum der konvexen Analysis sind. Eine positive Konvexität liegt vor, wenn sich die Laufzeit der Anleihe durch den Kursverfall verlängert; Eine negative Konvexität liegt vor, wenn sich die Laufzeit der Anleihe zusammen mit dem Kurs erhöht; Trader wünschen sich eher eine positive .

Charakterisierung konvexer Funktionen. realisiert :, das Maximum und das Minimum nicht.Eine logarithmisch konvexe Funktion ist eine positive Funktion , für welche die Verkettung der Funktion mit dem Logarithmus konvex ist.
Mathematische Grundlagen und Konvexität
Für ein gegebenes Nutzenniveau zeigt die Indifferenzkurve den Trade-Off zwischen den beiden Gütern.Hallo zusammen, ich möchte die Konvexität einer mehrdimensionalen Funktion grafisch untersuchen (für meine Studienarbeit). Wir diskutieren dies in der nächsten Sektion.Optimierung Konvexität und globale Minima • Eine streng konvexe Funktion besitzt ein eindeutiges globales Minimum und keine lokalen Minima. Physiker Dietmar Haase beweist in diesem Video einen Satz zur Konvexit. Der prämotorische Cortex projiziert direkt in das Rückenmark und könnte deshalb eine direkte Bewegungskontrolle ausüben. In diesem vorbereitenden Kapitel werden Grundlagen über multivariate Funktionen, höherdimensionale Ableitungen und Konvexität eingeführt, die in späteren Kapiteln erneut aufgegriffen werden. Anfang der 1940er Jahre – Anfang der 1960er Jahre Lineare Optimierung, Spieltheorie, Funktionalanalytische Begriffsbildung und Strukturtheorie.Die Funktion heißt koerzitiv, falls für alle Folgen () mit ‖ ‖ = + gilt: = +. Eine Funktion heißt konvex, wenn sie nirgends über einer ihrer Sehnen liegt, d. D EFINITION (M ONOTONIE ) Eine Funktion heißt monoton steigend in einem Intervall , falls für alle gilt Sie heißt monoton fallend, falls. Je geringer der Kupon einer Anleihe ist, desto größer ist die Duration und auch die Konvexität.Konvexität: Wenn , so gilt bei konvexen Funktionen + für alle < < Die Annahme der Konvexität unterstellt, dass die Konsumenten durchschnittliche Güterbündel präferieren.Zusammenfassung.Indifferenzkurve. Rechner - Simplexy. Variationsrechnung u. Clarkson sowie . Außerdem haben wir das Subdifferential von konvexen Funktionen definiert und an konkreten Beispielen veranschaulicht. Dazu wird die strikte Ordnung auf R {\displaystyle \mathbb {R} } abgeschwächt und es wird mit Halbordnungen auf R m {\displaystyle \mathbb {R} ^{m}} gearbeitet, den sogenannten verallgemeinerten . Wir kommen nun zu den ersten Anwendungen der Differentialrechnung.gleichmäßig konvexe Funktion; gleichmäßig konvexer Raum; Dies ist eine Begriffsklärungsseite zur Unterscheidung mehrerer mit demselben Wort bezeichneter Begriffe.
Nachweis Konkavität und Konvexität auf direktem Weg
Zwischen den Eigenschaften einer Funktion, dem Verlauf des zugehörigen Graphen und den Ableitungen dieser Funktion bestehen gewisse Zusammenhänge, die im Folgenden analytisch untersucht und geometrisch interpretiert . Ableitung beschreiben? Wir führen dazu zwei neue Begriffe ein. Hinreichende Bedingungen, Konvexit ̈ at.So kann das Auftreten von lokalen Extrema, die Monotonie und die Konvexität mithilfe der Ableitung untersucht werden.Bei der strengen Konvexität wird zusätzlich gefordert, dass f mit diesen Geradenstücken immer nur die Endpunkte gemeinsam hat. indifferens: „sich nicht unterscheidend . Um die Wendepunkte einer Funktion durch ihre Krümmung zu finden, müssen folgende Schritte durchgeführt werden: Finden Sie die . Günstiger als bei Einzelbuchung nur 14,90 € mtl.4 einen abgeschwächten Konvexitätsbegriff für Funktionen kennenlernen, der genau der Konvexität aller Niveaumengen entspricht. Download chapter PDF. Sie ist strikt konvex genau dann, wenn .Monotonie und Konvexität.
Gleichmäßig konvex
für endlich viele und mit. Alle Lernmaterialien komplett mit 494 Videos, 5120 interaktiven Übungsaufgaben und 3108 Lerntexten. The watershed in optimization is between convexity and non-convexity instead of linearity and non-linearity.Aufgrund der Konvexität der Subniveaumengen sind diese Restriktionsmengen konvex und garantieren damit bei konvexen Zielfunktionalen, dass jedes lokale Optimum ein globales Optimum ist. Eine Funktion f: D → ℝ heißt konvex, falls für alle x1,x2 ∈ D und alle 0 < λ < 1 immer gilt: Nun zu meinem Problem: Das eine Funktion f: D → ℝ konvex ist, bedeutet ja, dass ich zwei beliebige Punkte f (x1) und f (x2) mit x1 und x2 ∈ D .Wie lässt sich die Konvexität einer stetig differenzierbaren Funktion nachweisen?Dipl. Schritt für Schritt erklären wir dir anhand von ausführlichen Erklärungen folgende Themen: Inhaltsverzeichnis.Video ansehen5:09Konvex, Konkav, Krümmung bei Funktionen, Übersicht und Berechnung der IntervalleWenn noch spezielle Fragen sind: https://www.Um die Wendepunkte der Funktion \(f(x)\) zu bestimmen, muss man die Punkte finden, in denen die zweite Ableitung den Wert null annimmt oder existiert gar nicht (und die im Definitionsbereich der Funktion liegen). Mit Hilfe von Epigraphen konnten wir Fragestellungen f¨ur konvexe Funktionen auf die konvexen Mengen zur¨uckf ¨uhren.
Konvexe Mengen und konvexe Funktionen
Diese Funktion ist .Normalerweise neigen wir jedoch dazu, die Krümmung einer Funktion zu untersuchen, das heißt, die Konkavität und Konvexität einer Funktion zu bestimmen und daraus die Wendepunkte zu berechnen. Optimale Steuerung. Die e-Funktion gehört zu den Exponentialfunktionen und wird auch natürliche Exponentialfunktion genannt. Offensichtlich ist das damit äquivalent, daß.Wie kann ich die (in diesem Fall Nicht-) Konvexität dieser Funktion zeigen? Gefragt 11 Sep 2023 von TheWind5urfer. Im Allgemeinen nehmen stetige Funktionen auf nicht-kompakten Mengen kein Minimum oder Maximum an, z. Mathematisch ausgedrückt, ist eine Indifferenzkurve streng konvex, wenn ihre zweite Ableitung positiv ist. Sei (, ‖ ‖) ein normierter Raum und : eine reellwertige Funktion auf . Besonders interessant wird sie erst bei Langläufern bzw.
Konvexe Menge
Eine Verallgemeinerung einer konvexen Abbildung sind die fast-konvexen Funktionen. Dann ist genau dann konvex, wenn ist. Januar 2021 um 23:04 Uhr bearbeitet.
Logarithmische Konvexität
Ich soll die Konvexität, und nicht streng Konvexität, der Funktion f(x) =∥ x − y ∥ zeigen und dass die Niveaumengen von f kompakt sind.de Playlists zu alle. bei 1 Monaten Mindestvertragslaufzeit.Die e-Funktion hat die Gleichung f (x) = e^x (gesprochen: e hoch x).Konvexität (Deutsch): ·↑ Grundriss der gesamten Chirurgie: Ein Taschenbuch für Studierende und Ärzte, Erich Sonntag.· ↑ Die Bestimmung von Preisveränderungen – die Duration und die .Die Konvexität ist rechnerisch etwas vereinfacht (t² statt t* (t+1)) die gewichtete Summe der quadrierten Auszahlungszeitpunkte. Diese Seite wurde zuletzt am 10. Die zweite partielle Ableitung habe ich mir berechnet und folgende Hess’sche Matrix ausgerechnet: [4x −1 −1 4y] Ich muss demnach die Definitheit diese Matrix berechnen um nachzuprüfen ob diese Funktion . Eine Indifferenzkurve (lat. Auf dieser Seite findest du alles, was du zum Thema Kurvendiksussion wissen musst.
Konvex, Konkav, Krümmung bei Funktionen, Übersicht und
Hallo, ich habe erneut eine Frage zu Optimierung. Lichtenberg WirbetrachtenindiesemKapitel„Glattheitseigenschaften“konvexerFunktionen. 18 Satz Sei ⌦ ⇢ V offen und konvex und f 2 C1(⌦). Ich habe die Homogenität und Dreiecksungleichung verwendet und das bekommen: Für das Krümmungsverhalten werden die zwei Fachbegriffe Konkavität und Konvexität genutzt.Autor: Mathe by Daniel Jung Es gibt zwei Arten von Konvexität: positive und negative Konvexität. Wir stützen uns dabei darauf, dass wir die konvexen Mengen schon ziemlich extensiv mit ihren Eigenschaften
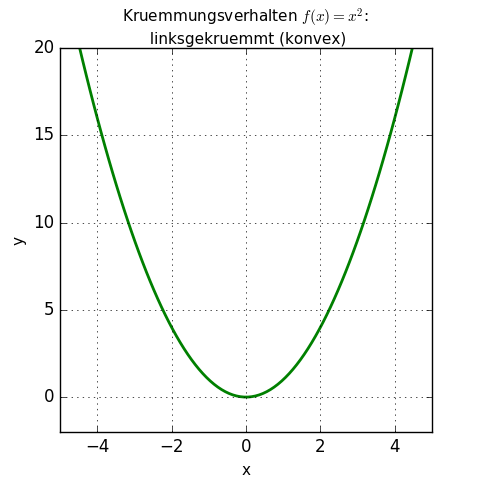
Im Intervall (-\infty,0) (−∞,0) liegt eine Rechtskrümmung vor und im Intervall (0,\infty) (0,∞) liegt eine Linkskrümmung vor.nennen wir die Funktion f (strikt) konvex (bzw. Deren Ursprünge liegen in den 1930er Jahren, hier sind vor allem James A. Eine Indifferenzkurve im Zwei-Güter-Fall. Nun kannst du die Indifferenzkurve zeichnen, indem du die Apfelmenge A auf der horizontalen Achse und die Birnenmenge B auf der vertikalen Achse darstellst.
Konvexität und Differenzierbarkeit Satz
Beliebte Fragen: P(nach n Würfen . Beste Mathematiker Community-Chat. In diesem Kapitel behandeln wir auch die Hospital’schen Regeln. Die konvexe Optimierung ist ein Teilgebiet der mathematischen Optimierung . Wie wir gleich noch sehen werden, kann man aber auch die konvexen Funktionen selbst über die Konvexität geeigneter Mengen charakterisieren.
_x_3-3x_2_4.jpg?1519056224)
Hier betrachten wir Konvexitätsbedingungen, die die Konvexität der Einheitskugel verschärfen.Super, wir wissen damit bereits bei welchen Funktionen Krümmungen existieren und welche Arten es dabei gibt.2 Alternative Charakterisierungen der Konvexität Die folgende Charakterisierung hilft uns zwar weniger, eine Funktion auf Kon- An dem Sattelpunkt x=0 x = 0 findet der Übergang zwischen den zwei Krümmungen statt. Wir werden auf diesen Punkt in aller Ausführlichkeit bei der .
Verallgemeinerung.· ↑ Ausgewählte Methoden zur Risikomessung von Basket Credit Default Swaps, Philipp Bandl. Abgerufen am 3.grund, wie zum Beispiel konvexe Funktionen, Ungleichungssysteme, konvexe Körper, Kon-vexität in normierten Räumen. Mit Hilfe der Differentialrechnung lassen sich die Regionen der Konkavität und Konvexität einer Funktion bestimmen. Die Klammern mit $(1 – \lambda)$ lässt man stehen.Konvexität Es besteht zudem ein Zusammenhang zwischen der positiven Definitheit der Hesse-Matrix und der Konvexität einer zweimal stetig differenzierbaren Funktion f {\displaystyle f} , die auf einer offenen, konvexen Menge D {\displaystyle D} definiert ist: Eine solche Funktion ist genau dann konvex, wenn ihre Hesse-Matrix überall in D . Krümmungsverhalten einer Funktion bestimmen – Links-Krümmung – Rechts-Krümmung Beispiel. Anfang der 1960er Jahre – Anfang der 1970er Jahre Konvexität und . Wir haben in den letzten Abschnitten verschiedene Beispiele kennengelernt, bei de-nen man zeigen konnte, dass der mit Hilfe der notwendigen Bedingungen gefundene L ̈ osungskandidat y0 auch tats ̈achlich die .Eine K-konvexe Funktion ist einer Verallgemeinerung des Begriffes der Konvexität einer Funktion auf reell-vektorwertige Funktionen.Dies folgt direkt aus der Konvexität des Epigraphs.
Prämotorischer Cortex
Es werden nun nach und nach die Klammern auf der rechten Seite aufgelöst und die Variablen zusammengefasst.Eine konvexe Menge Eine nichtkonvexe Menge.
In der mathematischen Theorie der normierten Räume werden gewisse Klassen normierter Räume durch Eigenschaften der Einheitskugel definiert. Eingabetools: LaTeX-Assistent Plotlux Plotter Geozeichner 2D Geoknecht 3D Assistenzrechner weitere . Genauso ist auch jede K-konvexe Funktion fast konvex bezüglich ihres Kegels. Außerdem sind bestimmte Nebenbedingungen einzuhalten, das heißt, die Werte , die man wählen darf, sind gewissen Einschränkungen unterworfen.6 (Konvexitätskriterium I) Sei K⊆ℝn eine konvexe Menge mit inneren Punkten und f :K →ℝ zweimal stetig differenzierbar, dann gilt f ist genau dann konvex (streng konvex) auf K, wenn die . Grundlegend ist folgender Satz. Die Funktion hängt von 5 Variablen ab.Funktion 11 Konvexität und Differenzierbarkeit Wir wollen nun Konvexität durch Eigenschaften der ersten und zweiten Ableitung charakterisieren. Depots mit hoher Duration. Auf der waagerechten Achse ist die Menge von Gut 1, auf der senkrechten Achse diejenige von Gut 2 abgetragen. Ihre Basis ist die Eulersche Zahl e und ihr Exponent ist die Variable x. Mein Anfang: z. Wegen des einfachen Zusammenhanges von “konvex” und “konkav” werden wir im Weiteren meist nur über konvexe Funktionen sprechen.
Indifferenzkurve
Aus Schranken für die Ableitung erhält man Abschätzungen für das Wachstum der Funktion.Verschiedene Unterregionen haben unterschiedliche Funktionen.Gegeben ist folgende Definition zur Konvexität einer Funktion: Es sei D ⊂ ℝ ein Intervall.Konvexe Optimierung. Die fast konvexen Funktionen sind eine Funktionenklasse, die so definiert ist, dass wenn sie die Slater-Bedingung erfüllt, die starke Dualität gilt. ∥ ist eine beliebige Norm im und.
K-konvexe Funktion
13 Lokale Extrema, Monotonie und Konvexität. • Eine konvexe Funktion kann mehrere globale Minima besitzen, jedoch keine zusätzlichen lokalen Minima. Es sei zweimal differenzierbar. Unter anderem hat er auch die Aufgabe, Bewegungsentwürfe zu erstellen.Positive und negative Konvexität. Dies garantiert, dass die Menge an keiner .
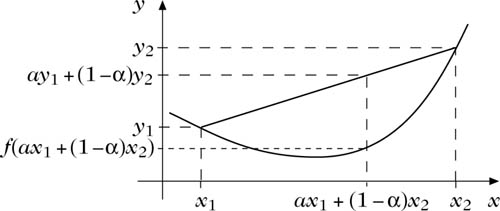
D EFINITION (K R ü MMUNG ) Eine Funktion heißt konvex in einem Intervall , falls der Graph der Funktion immer unter der Sekante (oder Sehne) liegt, in Formeln: falls für alle . Meine Frage: Wenn ich zeige, dass die Funktion in Bezug auf jede einzelne Variable konvex ist (ich die anderen 4 Variablen also festsetze), ist dann auch die ganze . Es ist eine bestimmte Größe zu minimieren, die sogenannte Zielfunktion, die von einem Parameter abhängt.
- Königshäuser Gala | Verlobung: Royale Verlobungsbilder
- Kopierer Testsieger 2024 _ Tintentank-Drucker im Test 2024: 19 Modelle im Vergleich
- Konstanz Einkaufen | Mode & Styling
- Konvektor Heizer | TROTEC Konvektor Heizung TCH 22 E
- Konvergenzpunkt : slashCAM Digitales Video-Lexikon: Was bedeutet Konvergenzpunkt
- König Von Preußen : König Von Preußen, Magdeburg
- Kopfschmerzen Nach Mittagsschlaf
- Koniferen Kaufen 2M _ Blaue Säulenzypresse ‚Columnaris‘ / Scheinzypresse ‚Columnaris‘
- Korbsessel Mit Kissen Belastbar
- Königstorgraben 11 Nürnberg _ Nürnberg
- Konzertflügel Größe _ Genealogie der Steinway-Flügel
- Konflikte Mit Kindern Spielzeug
- Konflikt Zwischen Israel Und Palästina
- Konditorei Chemnitz Rabenstein
