Konvergenzpunkt : slashCAM Digitales Video-Lexikon: Was bedeutet Konvergenzpunkt

Di: Samuel

Ein Häufungspunkt einer Folge (seltener: „Verdichtungspunkt“ oder „Häufungswert“) ist ein Punkt, der Grenzwert einer unendlichen Teilfolge ist.Konvergenzpunkt Der Punkt an dem sich die optischen Achsen (der Objektive bzw des menschlichen Auges) kreuzen. Aufgabe: f n (x) = \frac {sin (nx)} {n^2} n2sin(nx) mit x∈ℝ.Für die Rätselfrage Konvergenzpunkt haben wir Lösungen für folgende Längen: 11. Ab 250 m reduzierst du deine Treffgenauigkeit VOR dem Konvergenzpunkt, und du wirst auch NUR genau am .cc German-English Dictionary: Translation for Konvergenzpunkt.Fixpunktiteration.Eine Teilmenge A A eines metrischen Raums ( M M, d d) ist genau dann abgeschlossen, wenn jede konvergente Folge (a_n) (an) mit Werten aus A A gegen ein a\in A a ∈ A konvergiert. Sei (X,d) ein metrische Raum, a k eine Folge in X und a∈ X. Wir werden hier Dirichlet-Reihen nicht genauer besprechen, da sie nicht Bestandteil der meisten Analysis-Grundvorlesungen sind. siehe auch weitere Begriffe im 3D Glossar

Punktweise/ gleichmäßige Konvergenz

Jetzt nutzen für: Hausarbeien Bücher Abschlussarbeiten Kreuzworträtsel Geschichten und vieles mehr.

Reihen Konvergenz Rechner

gleichmäßige Konvergenz untersuchen.Wie zeige ich bei folgenden Funktionenfolge, dass diese punktweise konvergiert aber nicht gleichmäßig auf dem Intervall [0,1 . Um zu zeigen, dass ein beliebiger Häufungspunkt der Folge mit ihrem Grenzwert zusammenfällt, benutzt man eine analoge Schlussweise wie im Beweis zu Satz 5224B. Finde für uns die 2te Lösung für Konvergenzpunkt und schicke uns diese an unsere E-Mail (kreuzwortraetsel-at-woxikon de) mit dem Betreff Neuer Lösungsvorschlag für Konvergenzpunkt.Folgen sind Listen von Zahlen, die nach einer bestimmten Regel gebildet werden. Punktweise bzw.Ab 200 m beginnen sich die Flugbahnen vor und nach Konvergenzpunkt immer mehr aufzuspreizen. Zuerst geht es um die Waffenkonvergenzpunkt-Entfernung.Die Konvergenz in Verteilung, manchmal auch Konvergenz nach Verteilung genannt, ist ein Konvergenzbegriff, der aus der Stochastik stammt. Reihen hingegen sind die Summen der Glieder einer Folge.Der Fixpunktsatz von Banach, auch als banachscher Fixpunktsatz bezeichnet, ist ein mathematischer Satz aus der Funktionalanalysis, einem Teilgebiet der Mathematik. Diese haben wir oben gezeigt und die Grenzfunktion f (x)=0 f (x)= 0 ermittelt.

Folgen und Konvergenz

Im Gegensatz zu punktweiser Konvergenz erlaubt der Begriff der gleichmäßigen Konvergenz, wichtige Eigenschaften der Funktionen wie .2 (Folge von Funktionen) Eine Abbildung.Newtonverfahren für reelle Funktionen einer Veränderlichen Historisches über das Newtonverfahren. = 1/n 2 / ( 1/n 2 + x 2 ) und für n gegen unendlich und x≠0 geht das gegen 0 / x 2 = 0. Etwa die FW190-A1 ; BF109-F4 Reihe, aber auch für Rang II Fli. Schauen wir uns mal an, was dies für unsere harmonische . Definition (punktweise Konvergenz einer Funktionenfolge) Sei P ⊆ ℝ, und seien f n : P → ℝ für alle n.Aberrationen verbreitern den B. Daher ist sie punktweise konvergent gegen die Grenzfunktion f (x)=0 f (x)= 0.

Gleichmäßige Konvergenz und Funktionenräume

Die Funktionenfolge konvergiert also für alle Punkte x x aus ihrem Definitionsbereich. Die Abbildungswerte heißen Folgenglieder, und man schreibt. Wenn eine Folge von Funktionen in ist, so bilden für jedes die Funktionswerte eine Folge reeller Zahlen.2 Lemma: gleichmäßige Konvergenz)punktweise Konvergenz Sei M eine nichtleere Menge und (K,d

Konvergenzbereich

68) ein mit und für jedes mit gilt nun (und damit). die Antarktische, antarktische Konvergenz . Konvergenzgebiete sind Gebiete, also . Problem/Ansatz: Man soll die gegebene Folge auf punktweise bzw. Gleichmäßige Konvergenz zeigen. Zum Beispiel ist eine Folge, bei der jedes Glied um 2 größer ist als das vorherige.Konvergenz, Bündelung von (Licht-)strahlen. Hast du eine Verbesserung für . Konvergente Folge Sei ( )eine konvergente Folge mit lim →∞ = und ? ≔ 1 ( 1+ 2+⋯+ ).Finde ein anderes Wort oder Synonyme auf ein. Also liegen dann auch nur endlich viele .Eine konstante Folge mit für alle konvergiert gegen Genauso konvergieren schliesslich konstante Folgen gegen den Wert, den sie schliesslich annehmen.Dies bedeutet, dass eine Folge genau dann einen Grenzwert besitzt, wenn die Folgenglieder irgendwann beliebig nahe an diesem Grenzwert liegen. Die n-te Partialsumme ist dann die Summe aller Folgenglieder von 0 bis n .Aufgabe 5: (12 Punkte) Die funf Studierenden Tim, Tom, Tam, Tem und Tum wollen die Vorlesungen¨ ” Experimentalphysik“, ” Theoretische Physik“ und ” H¨ohere Mathematik“ h oren, und beschließen, dass an jeder Vorlesung mindestens einer von ihnen teil-¨

Folgen und Konvergenz

Somit ist die Aussage konstruktiv. Bei dieser Funktion ist man sich intuitiv nicht sicher, ob sie an der Stelle = stetig ist, denn in der Nähe davon schwingt die Funktion immer stärker.Ein Konvergenzbereich ist in der Analysis, einem Teilgebiet der Mathematik, einer Funktionenfolge oder (häufiger) Funktionenreihe zugeordnet und bezeichnet eine (oft auch die im Sinne der Inklusion maximale) Menge von Punkten im Definitionsbereich, in denen die Funktionenreihe punktweise konvergiert. Jedes Glied einer Folge () reeller Zahlen hat einen Index . Die Partialsumme hängt immer von dem Wert ab, bis zu dem du summierst. f (x) = lim n → ∞ f n (x) für alle x ∈ P.Many translated example sentences containing Konvergenzpunkt – English-German dictionary and search engine for English translations. heißt Folge von Funktionen oder Funktionenfolge.

geozentrische Bahnen heller Planeten - was bedeutet konkav / konvex ...

Konvergenz von Funktionenfolgen §2 Funktionenfolgen (2.3 (Punktweise Konvergenze) Eine . f n (x) = x 2 / ( 1 + (n*x) 2 ) = x 2 / ( 1 +n 2 * x 2) kürzen mit n 2 gibt.Häufungspunkt. 250 m aus allen Rohren treffen.

$Zentrale Sätze der Differentialrechnung – Analysis I (Kap. 1-9)$

Zeigen Sie, dass da-mit auch lim Für x=0 ist es f n (x) =0 für alle x, also auch Grenzwert 0. mit einer Funktion umgeformt werden.

Analysis I: 14 Funktionenfolgen

Es ist gleichsam ein Konvergenzpunkt von zwei einander ergänzenden Taten, die hier in einem einzigen beredten Zeugnis evangeliumsgemäßer Nächstenliebe vereint sind. zu einer Zerstreuungsfigur.

Konvergenz von Funktionenfolgen

Sie ist neben der Konvergenz .Guten Tag und frohes Fest allerseits , ich habe heute mal wieder eine kleine Hand voller Fragen. Dein zuverlässiges Wörterbuch für alternative Wörter mit gleicher oder ähnlicher Bedeutung. Konvergenz der in der Newton-Iteration erzeugten Folge zu einer Nullstelle ist also .php?title=Potenzreihe/Konvergenz_in_einem_Punkt/Absolut_gleichmäßige_Konvergenz_im_Radius/Fakt&oldid=920962“

Häufungspunkt

“Eine Folge (a i) i∈ℕ hat den Grenzwert a ∈ ℝ” oder “die Folge (a i) i∈ℕ konvergiert gegen a”, wenn (a−a i) i∈ .

Klothoide

3 Konvergenzverhalten von Fourierreihen 25 Ist P 1 k=0 a k eine Reihe von reellen oder komplexen Zahlen, c k >0, ja kj c k und P 1 k=0 c k0, so .Die Zahl ist der Grenzwert dieser Folge, falls für jedes > alle Glieder mit hinreichend großem Index „um herum“ in dem offenen Intervall (, +) liegen. Damit du die Grenzwertsätze nicht einfach blind glauben musst, findest du hier alle Beweise der Grenzwertsätze: Beweis von (1) Da (a n) und (b n) konvergieren, wissen wir, dass für alle zwei Zahlen existieren, für die gilt für alle und für alle .In der Analysis beschreibt gleichmäßige Konvergenz die Eigenschaft einer Funktionenfolge , mit einer vom Funktionsargument unabhängigen „Geschwindigkeit“ gegen eine Grenzfunktion zu konvergieren . Reihen werden in der Form angegeben, was bedeutet, dass du die Glieder von bis unendlich summierst. English-German online dictionary developed to help you share your knowledge with others. Isaac Newton verfasste im Zeitraum 1664 bis 1671 die Arbeit „Methodus fluxionum et serierum infinitarum“ (latein. Analog zum Konvergenradius von Potenzreihen, haben Dirichlet-Reihe, das sind Reihen der Form = mit , eine Konvergenzabszisse, so dass die Reihe für alle > konvergiert und für alle < divergiert.

Konvergenzbetrachtungen zum Newton-Verfahren

Die Folge konvergiert gegen Null, das heisst Denn für alle existiert nach dem Archimedischen Prinzip (Satz 2. lim n → ∞ a n = g. Wenn eine Folge einen Grenzwert besitzt, drückt dies ein Mathematiker auch dadurch aus, indem er sagt, die Folge konvergiert gegen . Eine Fixpunktiteration (oder auch ein Fixpunktverfahren) ist in der Mathematik ein numerisches Verfahren zur näherungsweisen Bestimmung von Lösungen einer Gleichung oder eines Gleichungssystems. Der Schwerpunkt bzw. Punktweise und gleichmäßige Konvergenz. Er gehört zu den Fixpunktsätzen und liefert neben der Existenz und der Eindeutigkeit eines Fixpunktes auch die Konvergenz der Fixpunktiteration. Welche Entfernung eignet sich, eurer Meinung nach, für Jagdflieger der Stufe 3. Fällt ein von einer punktförmigen Lichtquelle ausgehendes divergentes Strahlenbündel auf eine Sammellinse ( Konvexlinse ), die von der Lichtquelle einen Abstand hat, der größer als die Brennweite der Linse ist, so wird das divergente Lichtbündel in ein konvergentes verwandelt, dessen Konvergenz .In diesem Video ermitteln wir anhand zweier Beispiele, was der punktweise Grenzwert der Funktionenfolgen ist und wo bzw.Sei , dann gilt für alle nach der Dreiecksungleichung :. So sind nicht nur in der Analysis die punktweise Konvergenz und die gleichm¨aßige3) Satz Die Folge hf n: n 2Nivon reellen Funktionen mit Deﬁnitionsbereich A 2R konvergiert punktweise gegen die Funktion f : A !R genau dann wenn für alle x 2A und jedes . Da nach Satz 5729G eine konvergente Folge beschränkt ist, muss sie nach Satz 5729E wenigstens einen Häufungspunkt besitzen.

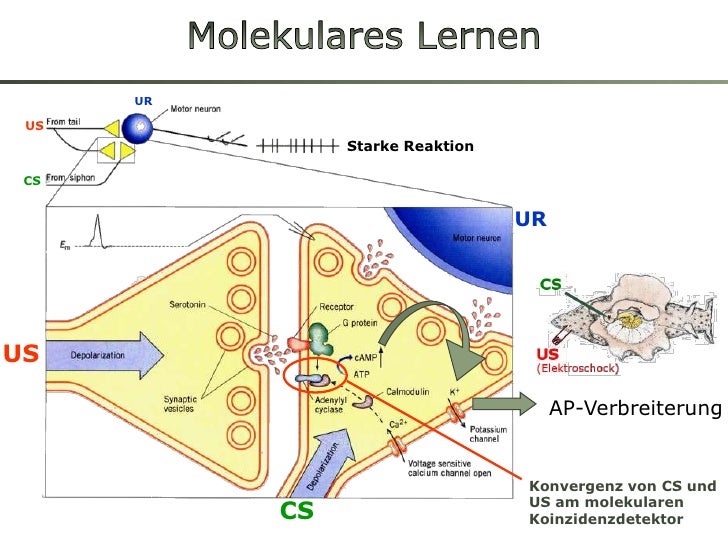
Lernen aus Neurobiologischer Sicht

2) Gleichmäßige Konvergenz.

9 Folgen und Reihen von Funktionen

Beide Begriffe sind eng miteinander verwandt. Wir sagen, dass die Folge a k gegen akonvergiert (Bezeichnung: a k k−→→∞ a), falls die reelle Folge d(a k,a) gegen 0 konvergiert, in der Sinne von Analysis 1.Konvergenzbetrachtungen zum Newton-Verfahren. Eine Folge a n nennt man konvergent mit dem Grenzwert g, wenn in jeder e -Umgebung von g fast alle Glieder der Folge liegen. das Intensitätsmaximum dieser Zerstreuungsfigur oder der B. Beantwortet 1 Jan 2018 von mathef 287 k ?.Konvergenz, Divergenz.Darin erklärt er einen neuen Algorithmus zum Lösen einer . Einerseits zeigen sie nämlich die Zuneigung der Einwohner dieser Stadt und der Pilger gegenüber dem Nachfolger Petri, und andererseits bringen sie die konkrete Solidarität .Maßtheoretische Konvergenzbegriﬀe Fur¨ Funktionenfolgen gibt es eine Reihe von Konvergenzbegriﬀen.

Fixpunktiteration

Der Konvergenzradius ist als das Supremum aller Zahlen definiert, für welche die Potenzreihe für (mindestens) ein mit konvergiert : Falls die Potenzreihe für alle reellen Zahlen bzw.

Konvergenz

Sei (X,d) (X,d) ein metrischer Raum.Konvergenz von Folgen Def. auf der ganzen komplexen Zahlenebene konvergiert, also diese Menge der (nach oben) unbeschränkt ist, sagt man, der Konvergenzradius ist unendlich: . Die Folge (a_n) \subset X (an) ⊂ X heißt genau dann beschränkt , wenn gilt: der Durchmesser der Menge aller Folgenglieder . Das Newton-Verfahren ist ein so genanntes lokal konvergentes Verfahren.L osung 32: (a) Wir stellen hier zwei L osungsm oglichkeiten dar: Es muss gelten (1 x) X1 n=0 a n x n =! ex = X1 n=0 xn n!: Die Reihe zur Exponentialfunktion ist absolut konvergent (*). [ Politik] wirtschaftliche Harmonisierung zwischen den Mitgliedsländern (und den Beitrittskandidaten) von Staatenbünden, besonders der Europäischen Union.Konvergenz und Funktionenräume §1 KONVERGENZ VON FUNKTIONEN Abbildung 1: Vorstellungsmöglichkeit des #-Schlauches 1. für: Von der Methode der Fluxionen und unendlichen Folgen).2 Gleichm¨aßige Konvergenz Sei Xeine nichtleere Menge, (N,d) ein metrischer Raum und (fn)n∈N eine Folge von Funktionen fn: X→ N. Folgen die keinen Grenzwert haben, heißen divergent.

Dein Nutzervorschlag für Konvergenzpunkt.Ferienkurs Analysis 1 Musterlösung zu Übungsblatt 2 Seite: 6 Zusatzaufgaben 8.Geometrische Summenformel. Schaut man sich den Graphen an, so sieht es (für mich) nicht nach einer gewöhnlichen Sprungstelle aus. Der wird meistens mit n bezeichnet.

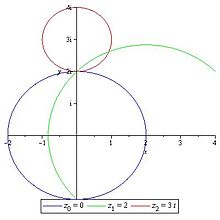
Konvergenzradius

In der Praxis heisst das für die E7: Bei Konvergenz 200 m kannst du von ca 50 bis ca.Grenzwert einer reellen Zahlenfolge Erläuterung und Definition Illustration des Grenzwertes einer Folge.Bildpunkt, bildseitiger Konvergenzpunkt der vom konjugierten Dingpunkt ausgehenden, durch ein optisches System konvergent gemachten Welle und Schnittpunkt der zu dieser orthogonalen Lichtstrahlen.

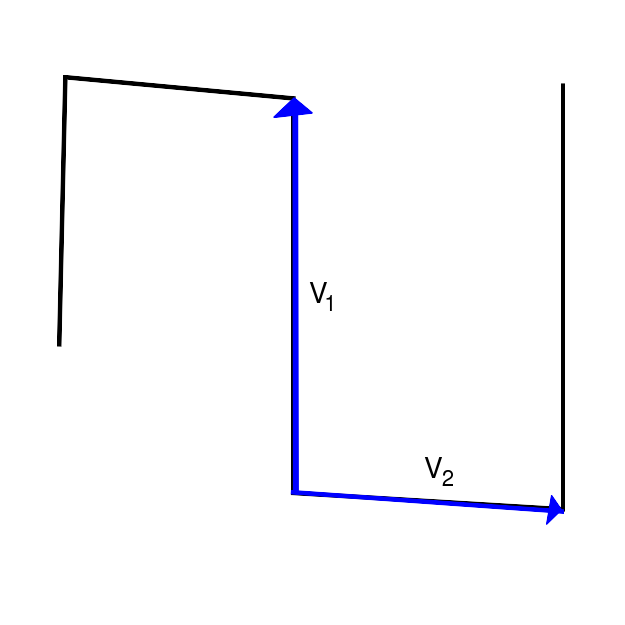
Der Begriff ,,Konvex``

[ Medizin] gleichsinnige Bewegung der Augen nach innen beim Sehen in unmittelbarer Nähe. Die Gleichung muss dazu zuerst in eine Fixpunktgleichung, also in eine Gleichung der Form.Ihr Graph ist: Graph der topologischen Sinusfunktion. ob diese Folgen auch gleichmäßig kon. f_(n)(x) = nx(1-x)^n Voraussetzung für die gleichmäßige Konvergenz ist punktweise Konvergenz. Damit haben wir gezeigt, dass .

Konvergenzpunkt :: German-English translation

Abgerufen von „https://de.Grenzwertsätze Beweis. x ∈ D in K existiert. Das bedeutet, dass sich der Wert der Folge für unendlich viele Elemente einem bestimmten Wert annähert.

Grenzwert (Folge)

Die geometrische Summenformel begegnet dir, wenn du sogenannte Partialsummen einer geometrischen Reihe berechnen sollst.Gleichmäßige Konvergenz zeigen | Mathelounge.a) punktweise ginge wohl so: Sei x∈ℝ.2 Die Funktionenfolge (fn)n∈N konvergiert auf Xgleichm¨aßig ge- gen die Funktion f : X → N,wenn f¨ur jedes ε>0 ein n0 ∈ N existiert, so dass

slashCAM Digitales Video-Lexikon: Was bedeutet Konvergenzpunkt

Kostenlos Reihenkonvergenzrechner – überprüfe unbestimmte Reihen auf Konvergenz Schritt für Schritt (punktweise Konvergenzbedingung) Dann heißt f : P → ℝ der Grenzwert der Funktionenfolge (f n) n ∈ ℕ und die Folge . Konvergenz ist die Eigenschaft von Folgen, dass sie gegen einen bestimmten Wert konvergieren. In der Analysis ist ein Häufungspunkt einer Menge anschaulich ein Punkt, der unendlich viele Punkte der Menge in seiner Nähe hat.

BAHTMZ

General