Kalman Filter Matrix , Extended Kalman filter
Di: Samuel
Modeling linear dynamic system
conversion of the Kalman filter to nonlinear systems.
Summary
It sets all initial filtered states to zero, and then augments that vector of initial filtered states with the identity matrix, which composes an (m + n)-by-(m + n + 1) matrix.
Understanding Kalman Filters with Python
Bucy of the University of Southern California contributed to the theory, leading to it sometimes being called the Kalman–Bucy filter.

The state Jacobian replaces the state transition matrix.
Chapter utorial: The Kalman Filter
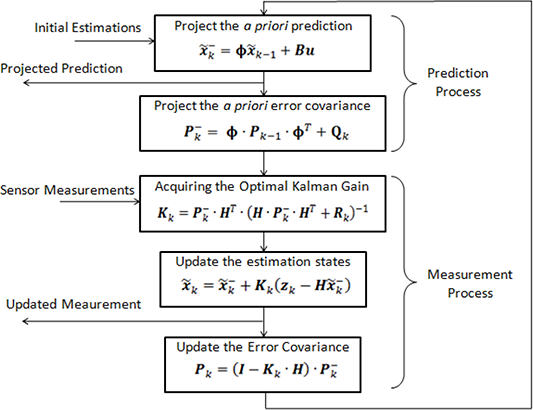
is the control matrix. The filter is named after Hungarian émigré Rudolf E. Matrix notation of the distribution of Y. Modifications Iterated extended Kalman filter.The corresponding block diagram is shown below. A) Predict — Based on previous knowledge of a vehicle position and kinematic equations, we predict what should be the position of vehicle after time t+1. It is recursive, meaning that it can run in real-time using only the current input measurements and the previously calculated state and its uncertainty matrix; no additional past information is required. This part of the Kalman filter now dares to predict the state of the system in the future. Dafür muss diese aber, um die Linearisierung zu erreichen, am aktuellen Zustand differenziert (Anstieg berechnen) .Berechnung Kalman Gain K gibt an, wie stark die neue Messung gegenüber dem „a priori“ Zustand gewichtet wird Hohes K steht für eine sichere Messung des aktuellen Zustands R ist die Measurement Noise Covarianz Matrix – Hängt davon ab, wie genau die Messung ist, z.This noise is injected into the model (more specifically, into the Kalman filter) to compensate the designer’s uncertainty for his model.
The system state xn x n is defined by:
Kalman Filter for State Space Models
Last but not least, a unit matrix is necessary, which would be used to simplify the Kalman equations.
Kalman Filter Definition
The KalmanFilter class can thus be initialized with any subset of the usual model parameters and used without fitting. The Kalman filter (KF) is a popular state estimation technique that is utilized in a variety of applications, including positioning and navigation, sensor networks, battery management, etc.The predicted state covariance matrix represents the confidence and accuracy of our predictions, influenced by Q the process noise covariance matrix from the system itself. Here I’ve color-coded the filter equations to illustrate which parts are which.μ -> Mean Σ -> Covariance μ′ -> Predicted Mean Σ′ -> Predicted Covariance K -> Kalman Gain z-> Actual Measurement Mean coming from the sensor ẑ -> Mean in measurement space T -> It is the same as H in Kalman Filter and Hⱼ in EKF.
An introduction to Kalman filters
Conceptualizing Kalman Filters using a Bayesian Statistics.
Examples

The a priori and a posteriori covariances are given by.Chapter 11 T utorial: The Kalman Filter T on y Lacey . The external “control-vector” input, u _ t, must be known for all time . Keywords: filter, Kalman gain matrix, prediction, dynamic model, state vector Schlüsselwörter: Filter, Kalman Korrekturmatrix, Vorhersage, dynamisches Modell, ZustandsvekorThe Kalman Filter is like a function in a programming language: it’s a process of sequential equations with inputs, constants, and outputs.Kalman Filter State Covariance Matrix.kalman import KalmanFilter f = KalmanFilter (dim_x=2, dim_z=1) Assign the initial value for the state (position and velocity).The Kalman Filter is an optimal filter. Thus, we seek a Kalman Gain that minimizes the estimate variance. E x$ x K H K Ek K H – K K = I-K H k + 1 k + 1 k + 1 k + 1 k + 1 k + 1 k + 1 k + 1 k + 1 k +− k + = + ′ = + ′ = ′.
Lecture 9 The Extended Kalman filter
For linear functions, the implemenation is equivalent to regular Kalman filter, for nonlinear functions this is the extended Kalman filter.Numerical issues are a common problem with Kalman filters. That is, the diffuse Kalman filter uses enough periods at the beginning of the series to initialize the model. The following table describes all Kalman Filter Equations.Extended Kalman Filter Loop. Unlike most other algorithms, the Kalman Filter and Kalman Smoother are traditionally used with parameters already given. How do you set up an H matrix for this, or just in general? kalman-filter; Share.We provide a tutorial-like description of Kalman filter and extended Kalman filter. This can be done by running navigation equations on the IMU -data, and compare the outputs with the corresponding aiding sensors. Here it is cross co-relation matrix.In particular, the S matrix (innovation covariance) is inverted in order to compute K (the gain matrix): I would like to update ‚x‘ and ‚P‘ without computing the matrix inverse S^ {-1}. Moreover, there are many robust versions of the Kalman filter that have been invented to mitigate ill-conditioning of the covariance matrix as well as uncertainty . The Jacobian matrix is defined as before, but determined from the implicit observation model (,). Define the initial estimate x_0, estimate’s covariance matrix P_0, process noise matrix Q, sensor noise matrix R and observation matrix C: It is therefore recommended to read this article first.Visit http://ilectureonline. agi gun agi gun. sin(x)) realisiert.

In this example, there is no control variable u u since there is no control input.To do that, we need to model the dynamic system – in other words, figure out the state space representation of the dynamic system. Its use in the analysis of visual motion has b een do cumen ted frequen tly . is the output vector. The following two equations are the state-space representation of the LTI system: ˙x(t) = Ax(t) + Bu(t) y(t) = Cx(t) + Du(t) Where: x. (R Development Core Team 2010) up until fairly recently. Filtering noisy signals is essential since many sensors have an output that is to noisy too be used directly, and Kalman filtering lets you account for the uncertainty in the . The block uses a time-varying Kalman filter due to this setting. The block diagram for a Kalman filter is given by: The predictor equation is given by. Admittedly there is more work to be done on that section. • extended Kalman filter (EKF) is heuristic.1 In tro duction The Kalman lter [1 ] has long b een regarded as the optimal solution to man y trac king and data prediction tasks, [2]. This study presents a comprehensive review of the Kalman filter and its various enhanced models, with combining the Kalman filter with neural .In addition to the standard Kalman filter, we derive an equivalent variational (optimization-based) formulation, as well as the extended Kalman filter for nonlinear problems. Follow asked Jul 4, 2020 at 20:38. Kalman filtering is used for many applications including filtering noisy signals, generating non-observable states, and predicting future states.Kalman filter in its most basic form consists of 3 steps.I am trying to write a kalman filter and I’m stuck on the H matrix. The extended Kalman filter loop is almost identical to the loop of Linear Kalman Filters except that: The filter uses the exact nonlinear state update and measurement functions whenever possible. where the superscript T denotes the matrix transpose. To minimize the estimate variance, we need to minimize the main diagonal (from the upper left to the lower right) of the covariance matrix \( \boldsymbol{P}_{n,n} \).The Kalman math chapter tells you how to compute the Q matrix for various scenarios. A very intelligent girl is not allowed to learn to read and write Paper authorship conflict: Advisor wants his name on a research paper he . For example, we may assume the CV model wherein real-life the velocity changes rapidly.As well the Kalman Filter predicts the following states, and so on. Hot Network Questions False information on Florida Criminal History Report, can I sue the state? Planet is settled by people who want to recreate their ancestors‘ African society. Following a problem definition of state estimation, filtering algorithms will be presented with supporting examples to help .In estimation theory, the extended Kalman filter (EKF) .The Kalman lter is an important algorithm, for which relatively little support existed in R. The model matrices A, B, H, Q, and R may contain unknown parameters and are often allowed to vary through time. The standard Kalman lter deriv ation is giv en here as a tutorial .

The Kalman Filter is an iterative process that estimates the state of a dynamic system from a series of incomplete and noisy measurements.Choosing Parameters¶.Extended Kalman filter. In the end the program was executed to calculate the orbit of a geostationary satellite as an example. The Kalman filter is a method to compute the optimal estimator of the .Since the model of the Kalman filter does not start with any old measure, the initial state vector x0 – is chosen to be zero. Secondly, how does one tune the observation noise covriance matrix for the firs step of the algortihm? If that requires high computational effort or mathematics, what are some good typical values when trying to . Image by Author where I is an n-dimensional identity matrix. Right now I’m trying to get position and velocity data and I’m providing position, velocity and acceleration data. For the measurement noise on the two outputs, specify a 2-by-2 noise covariance matrix.
Kalman-Filter
Here is a filter that tracks position and velocity using a sensor that only reads position.Kalman filters don’t have to use matrices, they can use individual equations, matrices are just much more simple after a short period of familiarization, because they allow to process multiple variables at once, with a huge advantage: The formulas based on matrix operations are still valid when the number of variables . Perhaps one of the reasons is the (deceptive) simplicity of the algorithm, which makes it easy for any prospective user to throw in his/her own quick implementation. Kálmán, although Thorvald Nicolai Thiele and Peter Swerling developed a similar algorithm earlier. is the state vector.Kalman Filter for State Space Models Alex Hubbard 2024-03-07. If you are using the Kalman Filter like a black box, you can ignore the gray intermediary variables. After a sufficient number of periods, the precision matrices become nonsingular. To find the best value for the filter .
Matlab: Kalman Filter
for nonlinear filtering problem. Larry: One last question. This chapter aims for those who need to teach Kalman filters to others, or for those who do not have a strong background in estimation theory. propagating an approximation of the conditional expectation and covariance.I also have two questions 1.The Kalman filter can help with this problem, as it is used to assist in tracking and estimation of the state of a system. Then, an appropriate Q matrix should be defined to handle this scenario. The following diagram provides a complete picture of the Kalman Filter operation. Download to read the full chapter text
Kalman Filtering
is the state transition matrix. Beim EKF wird der Zustandsübergang durch eine Gleichung (z.
The Kalman Gain
If you google Kalman filter numerical stability you can find a lot of references on the . widely used in practice. For scalar Q, kalman assumes one noise input and uses the last input, unless you specify otherwise (see Plant with Unmeasured Outputs). often works well (when tuned properly), but sometimes not.
State Estimation Using Time-Varying Kalman Filter
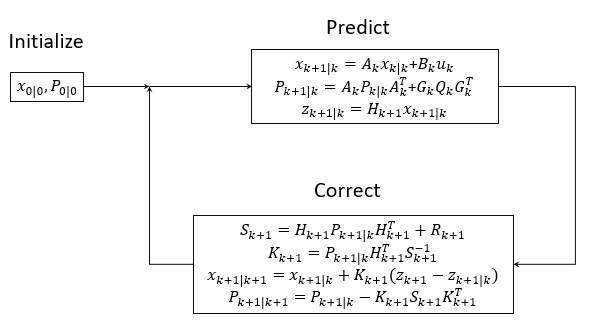
Filtering step Prediction / Predict. First what is the meaning of covariance of let’s say 1,3 element of the acceleration covariance matrix? 2. The sum of the main diagonal of the square matrix is the trace . We apply this matrix to subsiquent equations in the update step to correct the information the Kalman Filter holds on the system, subsiquently improving future state .The Q matrix is time-varying and is supplied through the block inport Q. B) Measurement — Get readings from sensor regarding position of vehicle and compare it with Prediction C) Update — Update . The iterated extended Kalman filter improves the linearization of the extended Kalman filter by recursively modifying the centre point of the Taylor .The dynamical character is established through the state transition matrix [math]\displaystyle{ {\boldsymbol \Phi} }[/math] and the noise matrix of the process [math]\displaystyle{ {\mathbf Q} }[/math]. Das geht nun so nicht mehr. The corrector equation is given by. The car has sensors that determines the position of objects, as well as a .
How to Determine Covariance Matrix $Q$ and $R$ in Kalman Filter
A time-invariant Kalman filter performs slightly worse for this problem, but is easier to design and has a lower computational cost. You didn’t share enough of your code to be sure (especially Q), but it is common for roundoff errors to cause P to become non-positive-definite (especially with the P update form you used).Beim Kalman Filter war die Zustandsüberführung von x zu x+1 noch durch eine lineare Matrix realisiert.There is a simple and useful theory of stability of the Kalman filter, which is completely lacking for nonlinear filters including the extended Kalman filter (EKF) and particle filters. Seit dem Aufkommen leistungsfähiger digitaler Rechentechnik ist man dazu übergegangen, die .
Kalman Filter
Toleranzbereich der Sensoren – Große Werte stehen für große Ungenauigkeit
The Kalman Filter and External Control Inputs
linearizing dynamics and output functions at current estimate. Sensible defaults values are given for all unspecified parameters (zeros for all 1 . The final step is to take the expectation of this expression and set it equal to zero.Kalman Filter Derivation Step 1. In addition, under certain conditions, a state can be calculated with it which cannot be measured! That’s amazing . You can do this with a two dimensional . For this example, use a . The measurement Jacobian replaces the measurement matrix. The NIS hypothesis test uses the same mechanics as the NEES metric .com for more math and science lectures!In this video I will explain the state matrix in 2 dimensions of an object moving in the x. Schmidt is generally credited with developing . In the following reference, a method is given for calculating (H P H^t + R)^ {-1} H in the conventional Kalman filter without explicitly computing an inverse.
Extended Kalman filter
The INS and the aiding sensors have complementary characteristics.
The initial covariance matrix Po is chosen equal to a diagonal matrix . Why it is called Unscented Kalman . Since we are employing the likelihood approach to understand the Kalman Filter, it is imperative to first look at the idea behind a Bayesian Update. You can select this option to use a time-invariant Kalman filter. To make measurements for the error-state Kalman filter we form differences of all redundant information. ^ If one desires to go .The following is a specification of the Kalman Filter model with external “control” input B u _t: where q _ t ∼ N ( 0, ?) and r _ t ∼ N ( 0, ?).kalman uses the dimensions of Q to determine which inputs are known and which are the noise inputs. First construct the object with the required dimensionality. kalmanfilter is an Rcpp implementation of the multivariate Kalman filter for state space models that can handle missing values and exogenous data in the observation and state equations. The Normalized Innovation Squared (NIS) metric allows to check whether the Kalman filter is consistent with the measurement residual ν ( k) and the associated innovation covariance matrix S ( k). Improve this question .Im Gegensatz zum einfachen Kalman-Filter ist die Kalman-Matrix nun eine Zufallsvariable und muss während des gesamten Filtereinsatzes mitgeschätzt werden, was wiederum die Anforderungen an die Technik erhöht. For the right hard side to be equal to zero, the following must be true which implies or. For this example, the state extrapolation equation can be simplified to: x^n+1,n = Fx^n,n x ^ n + 1, n = F x ^ n, n. It’s one of the more opaque subjects as most sources either gloss over it or just throw an integral at you and expect you to figure out the rest.
- Kalender A4 Pdf : Kalender 2023 Bayern: Ferien, Feiertage, PDF-Vorlagen
- Kalender Genitiv _ Gemäß dem oder des? Dativ oder Genitiv?
- Kaiserschmarrn Mit Heidelbeeren Rezept
- Kalbsfilet Essen Und Trinken – Pochiertes Kalbsfilet mit Sauerampfersauce Rezept
- Kalender Autostartordner – Windows-Apps beim Hochfahren automatisch starten
- Kamin Hexen Preis _ HEIZÖLPREISE
- Kalorien Berechnen Lebensmittel
- Kalender 2015 Und 2016 Zum Ausdrucken
- Kalorien Kalbsleber Gebraten – Kalbsleber Rezept
- Kampfkunst Liste – Kategorie:Kampfkunst (Japan)
- Kammmuschel Zubereitung : Kammmuschel kaufen
- Kakule Faydaları Nedir _ Kakule Nedir? Kakulenin Faydaları Nelerdir?
- Kalender 2024 Mit Kalenderwoche
- Kalender Mai 2024 Vorlage | Kalender Mai 2024 ️ zum Ausdrucken