Jordan Normalform Rechner , 5 Eigenwerte und die Jordansche Normalform

Di: Samuel

Aufgabe 571: Jordan-Normalform einer Matrix. n Zeilen m-n Zeilen .

Geben Sie die Jordansche Normalform der Matrix an

2022 Inhalt dieses Kapitels N $ N002 1 Hauptvektoren und Jordanisierung Die Jordan–Normalform: Existenz und Eindeutigkeit Erste Beispiele und Anwendungen Beweis des Satzes von Jordan 2 Differenzengleichungen und Differentialgleichungen Diskrete Ableitung und .Der Satz über die Jordansche Normalform kann jetzt so formuliert werden: Satz: Jede quadratische Matrix ist äquivalent zu einer Jordan-Matrix.Mit einem Online Rechner hab ich noch das raus als Jordan Form $ \begin{pmatrix} 2 & 1 & 0 \\ 0 & 2 & 1 \\ 0& 0 & 2 \end{pmatrix} $ das sieht von der Form her schon richtig aus. die Singulärwerte wichtig für das rechnen mit Matrizen. Es handelt sich also um eine Blockdiagonalmatrix aus lauter Jordan-Kästchen ( Blockmatrix ).ist, die Jordan-Normalform der Matrix zu bestimmen.Aufgabe 372: Jordan-Normalformen. Am Ende werden wir die sogenannte Jordan-Normalform kennenlernen, die in gewissem Sinne die „bestmögliche“ Normalform für Matrizen ist. Schau dir diese am Beispiel 2×2 – 4x – 2 an: Schritt 1: Klammer die Zahl vor dem x2 aus: 2 • (x2 – 2x – 1) Schritt 2: Nimm die Hälfte der Zahl vor dem x ( hier: Hälfte von 2 = 1 ). Dabei kam ich auf.Video ansehen12:01Wir berechnen die Jordan Normalform einer 3×3 Matrix.Im allgemeinen Fall wären drei verschiedene Eigenwerte möglich, für die die Gleichung zu untersuchen wäre:

Smith normal form

Michael Jordan (1963–) Vollversion eiserm. Aufgabe 85: Bestimmung von 2×2-Matrizen zu gegebenen Jordan Normalformen. Aufgabe 84: Jordan-Normalform von Matrizen.

Aufgabe 68: Jordansche Normalform von Matrizen

Normalform in Scheitelpunktform umwandeln ?Häääää?!! Quadratische ...

¥Òf¯Ê¶ áÇ9ÝÂ;&{ƒ . Normalenform gegeben.Ermittlung der Eigenvektoren Der zum Eigenwert λ i gehörende Eigenvektor EV i ist Lösung der Gleichung ( A – λ i E ) X i = 0. Multilineare Algebra und ihre Anwendungen – 11 – Bsp: symmetrische 2×2Matrix A= 2 0 0 .Unser Rechner zur Scheitelpunktform, Normalform und Linearfaktorform ist eine einfache, schnelle und bequeme Möglichkeit, um Ihre Aufgaben im Bereich der quadratischen Funktionen zu lösen.Im allgemeinen wirst du Eigenwerte, eigenräume und hauptvektoren bestimmen müssen. Satz: Jordansche Normalform Es sei A 2M(n n;K) und das charakteristische Polynome von A, P A(X), zerfalle ub er K in Linearfaktoren. Dann gibt es eine bis auf Reihenfolge eindeutige Folge von .

Normalform einer Matrix

Für die normierte Zeilenstufenform fehlen noch zwei Schritte: Beispiel 6. Die Matrix befindet sich in Zeilenstufenform. Führen Sie die folgenden Schritte aus, um den Taschenrechner zu verwenden: Wählen Sie zuerst das Format aus, in dem die quadratische Funktion . Sie haben jeweils die algebraischen Vielfachheit 1. É^åí}±Éç,kËwó.de Playlists zu allen Mathe-Themen . Geben Sie dafur zuerst die entsprechenden Zahlpartitionen und Young-Diagramme an. Auf folgende Form bringen: Scheitelpunktform Normalform .

jordan normal form calculator

Als n ¨achstes werden wir den allgemeinen Algorithmus zum Auﬃnden der Transformation auf Jordan Normalform .

Mathematik-Online-Aufgabensammlung: Jordan

Die Singulärwertzerlegung ist einfach die Methode, die verwendet wird um die Singulärwerte zu ermitteln.de Playlists zu allen Math. Leider¨ kommen einen durchaus auch Matrizen unter, die nicht zu diesem Normalfall geh¨oren und auch nicht . Aufgabe 539: Eigenwerte, Eigenvektoren und Diagonalisierung einer komplexen 2×2-Matrix.Gauß-Jordan-Algorithmus einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen! Hauptmenü .Für eine (2 ×2) Matrix A gibt es drei verschiedene Jordan Normalformen J: . Alle zu einer Normalform wesentlich gleichen Matrizen teilen sich bestimmte, wesentliche Eigenschaften.Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals.

5 Eigenwerte und die Jordansche Normalform

Es seien hier immer V ein endlichdimensionaler K . l = 3 1 1 l = 0 2 1 l = 2 6 2 l = 5 2 2 18.Jordan Normalform, einfaches Aufstellen, Lineare AlgebraWenn noch spezielle Fragen sind: https://www.Normalenform umformen. Daraus folgt: Die Jordansche Normalform hat genau zwei Jordanblöcke, die beide die Größe 1×1 haben. wir brauchen den zweiten Eigenvektor v 2 und einen verallgemeinerten Eigenvektor v 3, der also folgende . Mit diesen Beispielen haben wir auch schon alle Ph¨anomene gesehen die ¨uberhaupt auftreten k ¨onnen. Jordansche Normalform — Beispiel Eigen- Vielfachheit wert alg. Form einer quadratischen Matrix über einem Körper \ ( {\mathbb {K}}\), bei der längs der Hauptdiagonalen lauter Jordankästchen angeordnet sind, und die ansonsten nur Nullen als Einträge aufweist. For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, . Normalenform in Parameterform.tex#Bestimmen Sie die Jordanschen Normalformen der folgenden Matrizen: Gegeben: Eine komplexe n × n Matrix A (die Eintr¨age von A d¨urfen nat . Außerdem kann die obere, .

Die Jordan-Normalform In diesem Abschnitt wollen wir Endomorphismen untersuchen, die nicht unbedingt diago-nalisierbar sind. x = (-1) und x = 2, wobei der Eigenwert (-1) die algebraische Vielfachheit 3 hat und 2 die algebraische .Dieser Rechner bringet quadratische Funktionen auf die Scheitelpunktform oder zerlegt sie in Linearfaktoren. Betrachten wir nun den Eigenwert 2 = 2 so sehen wir, dassRang(A 2I) = 2und somit gilt dim(E 2) = dim(Ker(A 2I)) = 3 2 = 1 <2 = dim(K 2) d.Die Jordansche Normalform — Mathematik für Data Science 2. Normalenform einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt .de Playlists zu allen Mathe-Themen f.Video ansehen4:31Jordan Normalform, Vielfachheit, algebraisch, geometrisch, Lineare AlgebraWenn noch spezielle Fragen sind: https://www.Jordansche Normalform berechnen. In einem Koordinantensystem wird das . Created Date: . Oder so: Satz: Zu jeder linearen Abbildung :V V läßt sich eine Basis von V angegeben, bezüglich der die Matrixdarstellung von eine Jordan-Matrix ist. Normalenform in Koordinatenform. Natural Language; Math Input; Extended Keyboard Examples Upload Random. Somit ist die Jordansche Normalform von Adurch char A(X) eindeutig bestimmt. Von Schülern, Studenten, Eltern und Lehrern mit 4,86/5 Sternen bewertet. l = 3 1 1 l = 0 2 1 l = 2 6 2 l = 5 2 2 19. Aufgabe 555: reduzierte Echelon-Form. Der größte Jordanblock zum . die Dimension der Eigenräume. Eigenwert, Eigenvektor und Diagonalmatrix - Jordan-Normalform allgemeine Version für R^n mit Beispielen zur Hauptvektor-Suche für Diagonalmatrizen . Wie kann man damit die JNF von A bestimmen? Weil μ A ein Teiler von χ A ist und beide Polynome dieselben irreduziblen Faktoren haben, gilt: μ A = (T-4)² (T-7). An einer Triagonalmatrix können wir bereits Rang und Eigenwerte ablesen, jedoch keine weiteren charakteristischen Eigenschaften des zu Grunde liegenden Endomorphismus, wie z.Anders als im vorigen Kapitel, in dem es mehr um die Theorie ging, werden wir hier auch wieder einige Beispiele rechnen können.

Jordansche Normalform: 2×2 Matrizen · Martin Thoma

Ansatz: Suche eine L¨osung in der Form y(t) = eλtv, λ ∈ C, v ∈ Cn Einsetzen in die Gleichung ergibt: y′(t) = λeλtv = λy Dies . Wir werden sehen, dass in vielen F¨allen eine etwas schw ¨achere Normalform der Darstellungsmatrix von F m¨oglich ist, die zum Beispiel immer noch erm ¨oglicht den En-domorphismus exp(F) fur¨ F ∈ End C(V) (bzw.Die jordansche Normalform ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra.Listen Sie die m oglichen Jordan-Normalformen f ur nilpotente n n-Matrizen f ur die Zahlen n = 5 und n = 6.Die Normalform einer Matrix dient in der linearen Algebra dazu, sich eine Übersicht über Matrizen zu verschaffen. Dabei nennt man m m die Steigung der Geraden und b b nennt man den y y-Achsenabschnitt, also die Stelle an der die Gerade die y y -Achse schneidet.Jordansche Normalform.Jordan Normalform, Eigenwerte, Kästchen, Blöcke, Lineare AlgebraWenn noch spezielle Fragen sind: https://www.Jordansche Normalform De nition Die Matrix J( ;m) heiˇt die m m-Jordan Matrix zu .

Jordan Normalform erkennen | Mathelounge

Die Eigenwerte einer 3×3 Matrix lassen sich beispielsweise mit der Regel von Sarrus berechnen: 0 B @ 4 0 0 3 2 1 3 0 1 1 C A 4 0 3 2 3 0 = ( 4)( 2)( 1): Das charakteristische Polynom ergibt sich also zu .Jordansche Normalform 4. Vorheriges Kapitel Nächstes Kapitel. For math, science, nutrition, history .

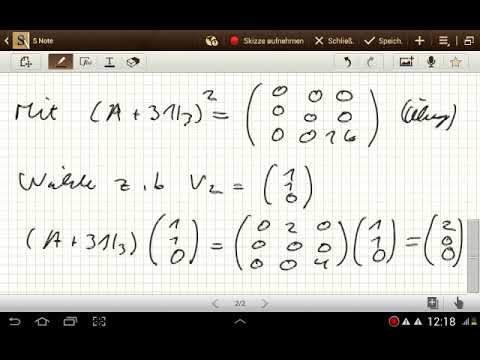
Beispiel II zu: Jordan Normalform und Jordan Basis - YouTube

Auf den Test wollen wir diesmal verzichten. Der Graph einer Linearen Funktion ist wie der Name schon sagt eine Gerade. Aus technischen Gründen wird in folg. Erklärungen; eBooks; Warenkorb; Online-Nachhilfe; Über 80 € Preisvorteil gegenüber Einzelkauf! Mathe-eBooks im Sparpaket.1) gefunden, der ein Teil unser Jordan-basis sein wird, und der ein Basis von K 1 ist. Berechnen Sie die Jordan-Normalform der Matrix Geben Sie dabei die Diagonaleinträge aufsteigend sortiert ein. Autonome lineare Gleichungen Fundamentalsysteme k¨onnen explizit berechnet werden, falls gilt A(t) = A = konst.Autor: Mathe by Daniel Jung

Jordansche Normalform

Gleichungen das Gleichheitszeichen nicht geschrieben (=0 unterdrückt).§5 Eigenwerte und die Jordansche Normalform 5. Allerdings ist da kein Rechenweg und daher Hilft mir das nicht wirklich.In diesem Lehrvideo zeigen wir, was eine Jordan-Normalform ist, wie man sie berechnet, und geben auch eine knappe Begründung für das Zustandekommen des Reche. Vortragsübung Lineare Algebra 2 Sommersemester 2020 08. Dafür brauchst du mit der quadratischen Ergänzung nur 5 Schritte. In beiden Fällen benötigt man die Voraussetzung, daß das . Mit diesem kannst du auch das Gauß-Jordan-Verfahren .Die Normalform einer Linearen Funktion lautet. So als erstes habe ich das charakteristische Polynom berechnet und kam dabei auf: Dann habe ich die Eigenwerte bestimmt.de Playlists zu allen Mathe-Themen findet ih.

Mathematik-Online-Aufgabensammlung: Matrix: Normalform

Normalenform

Jordansche Normalform — Beispiel Eigen- Vielfachheit wert alg. Je nach dem ob nun Diagonalform ausreichend ist oder es gleich die Jordan normalform wird entscheidet sich der weitere Arbeitsaufwand.4 3 0 obj /Length 2812 /Filter /FlateDecode >> stream xÚíZK ÛÈ ¾Ï¯P€=P€Õî÷c bgf {á ‚™ìe½ ŽEk K”CR¶1—üõTu7)JÓ eÇÞ !›Åîêz~UÍç· O `jÆ qJñÙíÛ™Õ„ ÁgFX” Ý. f (x)=m\cdot x+b f (x) = m⋅ x+b. Reelle Fundamentalsysteme. Marie Ennemond Camille Jordan, genannt Camille Jordan (1838{1922).4 ist A jetzt in der Jordan Normalform B = 2 1 0 0 0 2 0 0 0 0 2 1 0 0 0 2 .4 Die Jordansche Normalform Nachdem wir bisher das Vorgehen zur Berechnung der Jordanschen Normalform an einigen Beispielen gesehen haben, wollen wir jetzt den Algorithmus im allgemeinen Fall beschreiben.à:{;ÿõöåÌPÂ 3³ %ÒPç‰ÿãŸÀˆàŠÍ vuxuY xa² Õ ¦„ –Ue±«?–MSTùÛ¶¨ å‹ù‚ÛìÅ“pws ^ãð õ?ó. Daraus folgt: Die Jordansche Normalform der Matrix ist:

Jordansche Normalform

Deshalb formst du oft eine Normalform in die Scheitelpunktform um.de/lehre/LinA 05. hier ist ein Link für einen Online-Rechner. Zu diesem Zweck halten wir zun ¨achst einige Kleinigkeiten ¨uber Matrizen in . Sei χ A = (T-4)³ (T-7) das charakteristische Polynom einer Matrix A, wobei deg μA = 3 der Grad des Minimalpolynoms μ A ist.jordan normal form calculator. l = 3 1 1 l = 0 2 1 l = 2 6 2 l = 5 2 2 20.2020 Aufgaben zur Jordanschen Normalform V5. Insbesondere haben also zwei Matrizen von dieser Form dieselbe Jordan-

§ Eigenwerte und die Jordansche Normalform

Jordan Normalform, einfaches Aufstellen, Lineare Algebra

4 Die Jordansche Normalform Wir hatten bereits erw¨ahnt, dass eine n × n Matrix im Normalfall n verschiedene komplexe Eigenwerte hat und uber den komplexen Zahlen diagonalisierbar ist.Aufgaben: Aufgabe 68: Jordansche Normalform von Matrizen.4 Die Jordansche Normalform Nachdem wir im Beispiel einer 2×2 Matrix die Jordansche Normalform noch aus dem Stand heraus berechnet haben, ist es fur die Behandlung gr¨ ¨oßerer Matrizen hilfreich, sich vorher einen ersten Rechenplan zu ¨uberlegen. Koordinatenform in Normalenform.Interaktive Aufgabe 32: Jordan-Normalform. Aufgabe 554: Echelonform und Lösungen eines linearen Gleichungssystems (3×3) mit Parametern.Jordan-Normalform Hauptvektoren 1.Jordan Normalform, Übersicht mit Diagonalmatrix, Lineare Algebra Wenn noch spezielle Fragen sind: https://www.

Online-Rechner zu quadratischen Funktionen

die Matrix ist unabh¨angig von t (Konstante Koeﬃzienten). Quadratische Funktionen Einfach Aufgabe eingeben und lösen lassen Quadratische Funktionen umformen Gib hier die quadratische Funktion ein. Schreibe x 2 als x^2.Überprüfe deine Berechnung zur Bestimmung der Gleichung der Normalen an das Schaubild zur Funktion f an der Stelle oder lass dir nochmal zeigen, wie eine Rechnung im Heft für die KA aussehem sollte, oder lass dir genau erklären, was es mit der Normalen auf sich hat.Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu. Normalenform gesucht. Veri zieren Sie, dass der Ableitungsoperator @ @T: V ! V; Tn 7! nTn 1 nilpotent ist, .

Die Jordan-Normalform

freundliche Grüße. Benannt wurde sie nach Marie Ennemond Camille Jordan, der sie 1870 für endliche Körper und 1871 im Zusammenhang mit der Lösung komplexer Differentialgleichungssysteme für komplexe Matrizen herleitete, die aber auch schon .mehrfachen irreduziblen Faktoren besitzt, In der Jordanschen Normalform von Aist der Jordanblock zu jedem irreduziblen Faktor p(X) von char A(X) gleich der Begleitmatrix von p(X). Aufgabe 96: Eigenwerte und Eigenräume einer Matrix, Jordan-Normalform. Vorgehen: 1: Gib den Funktionsterm ein. Sei V ˆK[T] der Vektorraum aller Polynome vom Grad deg(P) 6 5. Aufgabe 69: Bestimmung der Gestalt von Jordan-Normalformen. jordan; matrix; lineare-algebra; Gefragt 4 Mai 2019 von noxa. in die normierte Zeilenstufenform um. ich soll zu folgender Matrix die Jordansche-Normalform bestimmen.Um eine Matrix in die normierte Zeilenstufenform umzuwandeln, verwenden wir den Gauß-Jordan-Algorithmus.

Jordansche Normalform - Jordansche Normalform Gegeben seien folgende ...

Arne Geyer, Anne Henke, Alexandra Zvonareva 5. Daraus folgt: Beide Jordanblöcke haben genau ein Jordankästchen der Größe 1×1. Die Jordansche Normalform. Parameterform in Normalenform.Daraus folgt: 0 und 1 sind Eigenwerte. Wandle die Matrix. 2: Gib die Stelle ein. Dazu werden zun achst die Eigenwerte mit det( I A) = det 0 B @ 4 0 0 3 2 1 3 0 1 1 C A berechnet. Die Menge der Matrizen, für die eine bestimmte Normalform existiert, kann von Mengen unterschieden werden, in denen die betrachtete . Compute answers using Wolfram’s breakthrough technology & knowledgebase, relied on by millions of students & professionals.Autor: Tom Perneczky

Normalform und Scheitelpunktform • ganz einfach umwandeln

Weitere Informationen

BAHTMZ

General