Ist Nullmatrix Diagonalisierbar
Di: Samuel
Die Vektoren 1 3 und 1 0 3 2 1 3 = 1 9 sind o enbar nicht kollinear. Reelle symmetrische Matrizen sind stets diagonalisierbar, fertig.
Nilpotente Matrix
Gilt immer, dass wenn A 2 = 0 ist, dass dann A diagonalisierbar ist? (wobei A∈K nxn und K ein beliebiger Körper) Mir würde kein Gegenbeispiel einfallen, denn A müsste ja hier die quadratische Nullmatrix sein, und diese sollte doch stets diagonalisierbar sein. Kommentiert 6 Dez 2018 von .t diagonalisierbar, wenn eine der beiden vorigen Bedingungen erfullt˜ ist. ist die Diagonalisierung ein eleme. Determinante = 0 2. Geben Sie in die Felder für die Elemente der Matrix ein und führen Sie die gewünschte Operation durch klicken Sie auf die entsprechende Taste aus.t diagonalisierbar, wenn der zugeh˜orige Endomorphismus LA: Kn! Kn mit LA(v) = Av diagonalisierbar ist (, A ist ahnlich zu einer Diagonalmatrix) . in der Logik und in der theoretischen Informatik ein Beweisverfahren, siehe Cantor-Diagonalisierung. des Matrizenraums. ich danke im voraus 🙂 matrix; Gefragt 6 Dez 2018 von lisa. Normale Matrizen sind diagonalisierbar. Ich hab mal mit dieser hier angefangen: ( 0 1 ). a)\( \begin{pmatrix} -1 & 1 & 1 \\ -3 & 3 &1 \\ -3 & 1 &3 \end{pmatrix} \) , b)\( \begin{pmatrix} -2 & 1 & 2 \\ -5 & 3 &3 \\ -4 & 1 &4 \end{pmatrix} \) Problem/Ansatz: diagonalisierbar; Gefragt 18 Jun 2020 von maher2020. Es sei A∈M22, ( ) eine zweireihige quadratische Matrix, welche nicht diagonalisierbar sei.
A transponiert diagonalisierbar
wäre eine Möglichkeit .
Welche matrizen sind diagonalisierbar?
Gefragt 2 Jun 2022 von dominik77. Matrix diagonalisieren | Lineare Algebra | Übungen und Aufgaben mit Lösungen | Erklärung mit Beispielen | PDF.Diagonalisierung. Liegt eine Matrix in der diagonalisieren Form vor, so können sehr einfach Potenzen von berechnet werden mit: diagonalähnlich = diagonalisierbar.
Matrix diagonalisierbar?
Diagonalmatrizen sind deshalb allein durch die Angabe ihrer Hauptdiagonale bestimmt.
Eigenwerte
Wir haben gerade eine Formel mit welcher wir eine Matrix diagonalisieren können. Es heißt unitär . Zuletzt: M ist diagonalisierbar, wenn es eine Matrix A gibt, so dass: A−1 ⋅ M ⋅ A = diag.Es ist unitär genau dann, wenn die Spalten von eine Orthonormalbasis von bilden. eine quadratische Matrix mit A n = 0 füe eine natürliche Zahl n. Determinante = 1 oder -1 6 Orthogonale Matrix .
Prüfen ob Matrix diagonalisierbar ist
Also ist die Aussage falsch, es muss eine unitäre Matrix U zur Matrix A geben. Spur = 0 5 Selbstinverse Matrix 5. der Anzahl linear unabhängiger Eigenvektoren zu einem Eigenwert. Gefragt 25 Jan 2021 von nattiamber. Deine Vermutung ist genau richtig.1 Definition A∗A = I n 5. Nicht diagonalisierbar insofern A nicht die Nullmatrix ist 4.A ist genau dann diagonalisierbar, wenn A transponiert diagonalisierbar ist. Die Definition schreibt also nicht vor welche Einträge die Hauptdiagonale hat.Ist der Exponent negativ, so müssen die Matrixelemente in einem Körper liegen.Überprüfen Sie, ob di folgenden Matrizen diagonalisierbar sind und diagonalisieren Sie diese gegebenenfalls.Eine hermitesche Matrix ist stets normal und selbstadjungiert, sie besitzt nur reelle Eigenwerte und sie ist stets unitär diagonalisierbar. Unter einer Dreiecksmatrix versteht man in der Mathematik eine quadratische Matrix, die sich dadurch auszeichnet, dass alle Einträge unterhalb (obere Dreiecksmatrix) bzw. Jetzt hab ich mir überlegt das ich eine Nilpotente Matrix nehme.Anschließend berechnet man die Diagonalmatrix über die Formel. Die Matrix A A muss nicht notwendigerweise die . Sie durfen w ahrend des L osens des Tests eine Formelsammlung verwenden. Jetzt wäre meine Frage: Gibt es noch eine weitere Möglichkeit wie man das Ganze noch einfacher . Jetzt sollt ich nur noch wissen ob sie wirklich nicht diagonalisierbar ist? ⇒ A ⋅ x = 0. Die Eigenwerte (oder Eigenwerte) .
Matrizen diagonalisierbar Überprüfen
Bei allen Aufgaben ist genau eine Antwort richtig.
Nullmatrix

Diagonalisierbare Matrix
Diagonalisierbarkeit einer Matrix
de Playlists zu allen Mathe-Themen f.Eine Diagonalmatrix ist eine Matrix, die sowohl obere als auch untere Dreiecksform hat .Nun soll ich begründen oder widerlegen, ob A diagonalisierbar ist.Zeige, dass A diagonalisierbar ist und bestimme eine invertierbare Matrix T mit.
Angenommen λ = 0.

Grundsätzlich würde man jetzt die geometrische Vielfachheit bestimmen und überprüfen, ob die mit den Eigenwerten übereinstimmt. reelle Eigenwerte mit alg. Da wir aber gesagt haben, dass x nicht der Nullvektor ist, sind nicht alle x1,x2 . Einheitsmatrix. ===> B ≠ diagonalähnlich, weil die dim Basis aus EV = 2. Ich bräuchte für eine Aufgabe eine Matrix die nciht diagonalisierbar ist.

(2) Sind ϕ und ψ halbeinfach, so ist auch ϕ+ψ halbeinfach. A – Id sei nilpotent.In diesem Abschnitt werden die Diagonalmatrix und die Rechenregeln für diese eingeführt.com/en/brightsideofmathsIhr werdet direkt informiert, wenn ich einen Livestream anbiete. Dabei sei D eine Diagonalmatrix.
Diagonalisierung
Vielfachheit 1 (die dann auch die geom. Und dann kann man die Eigenvektoren zu einer Matrix B zusammenfügen. Transponierung einer Matrix.
Eigenwerte, Diagonalisierbarkeit, charakteristisches Polynom
D = U * A * U -1.
A^2 = 0 => A diagonalisierbar?
Charakteristisches Polynom ausrechnen, Diskriminante \(>0\) (das geht ohne TR), also zwei versch.Mithilfe dieses Rechners können Sie die Determinante sowie den Rang der Matrix berechnen, potenzieren, die Kehrmatrix bilden, die Matrizensumme sowie das Matrizenprodukt berechnen.Diagonalisierbar 4.Eine quadratische Matrix bezeichnet man als nilpotent, wenn eine ihrer Potenzen die Nullmatrix ergibt: für ein.Kostenlos Matrix-Diagonalisierungsrechner – diagonalisiere Matrizen Schritt für Schritt A = ( 3 0 0 0 2 0 0 0 4) Diagonalmatrix. Als Diagonalmatrix bezeichnet man eine quadratische Matrix, bei der alle Elemente außerhalb der Hauptdiagonalen Null sind.
Matrixpotenz
Jetzt ist in einer meiner Übungen die Matrix. Zeigen Sie, A hat als einzigen Eigenwert die Null. Ich glaube sogar jede Matrix ist diagonalisierbar über C. angegeben, sowie die Eigenvektoren (3 , 1) t und (2 , 1) t . diagonalisierbar; eigenwerte .2 Eigenschaften 1. Die Matrix ist diagonalisierbar über C und nicht diagbar über R. oberhalb (untere Dreiecksmatrix) der Hauptdiagonale null sind.Eine quadratische -dimensionale Matrix heißt diagonalisierbar oder diagonalähnlich, wenn es eine Diagonalmatrix gibt, zu der sie ähnlich ist, das heißt, es existiert eine reguläre Matrix , so dass gilt bzw. Eine wichtige Klasse hermitescher Matrizen sind positiv definite Matrizen, bei denen alle Eigenwerte positiv sind. Welcher der folgenden Vektoren ist ein Eigenvektor von 1 0 3 2 ? (a) 3 1 . Eigenwerte 0 oder 1 4 Nilpotente Matrix 4. (Das ist genau dann der Fall, wenn A nur einen Eigenwert λ0 hat, welcher dann die algebraische Vielfachheit v0 =2 hat, wobei die Dimension des zugehörigen Eigenraums E0 gleich 1 ist [siehe Satz 27. Die Diagonaleinträge in sind hierbei die berechneten Eigenwerte und die Spalten von sind die zugehörigen Eigenvektoren. (ii) Eine n£n Matrix A hei.Abonniert den Kanal oder unterstützt ihn auf Steady:https://steadyhq. Rechenregeln für Matrizen.
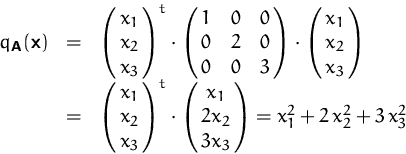
matrix; diagonalisierbar; invertierbar; eigenwerte; eigenvektoren + 0 Daumen. Ist der Zahlenbereich der Matrixelemente algebraisch abgeschlossen , kann man also darin beliebige algebraische Gleichungen lösen, so kann der Exponent auch rational sein und die Matrixpotenz kann über die Jordansche Normalform von A {\displaystyle A} auf . Zeigen Sie, alle Eigenwerte von A sind gleich 1. Diese Darstellung bildet die Grundlage für die . Insbesondere, ist hermitesch, so hat auf der Diagonalen reelle Einträge. Das bedeutet, die Dimension der einzelnen Eigenräume stimmt jeweils mit der algebraischen Vielfachheit der entsprechenden Eigenwerte im charakteristischen Polynom der Matrix überein. A invertierbar ⇔ ∃S, D: A = S−1DS, D Diagonalmatrix. Eine hermitesche Matrix mit reellen Einträgen ist symmetrisch . Entsprechend bezeichnet man einen Vektorraum-Endomorphismus als nilpotent, wenn es eine Zahl gibt, sodass die Nullabbildung ist.Matrix diagonalisieren, Beispiel, Matrixalgebra, Lineare AlgebraWenn noch spezielle Fragen sind: https://www. Kommentiert 24 Jan 2020 von wächter. (1) Sind ϕ und ψ diagonalisierbar, so ist auch ϕ+ψ diagonalisierbar. dann zeigen dass geometrische und algebraische vielfachheit bei A und A transponiert übereinstimmen.3 und Folgerung 27.Jede symmetrische Matrix ist diagonalisierbar D:=T^t A T Jede symmetrische Matrix ist orthogonal diagonalisierbar Jede symmetrische Matrix hat einen Eigenwert Alle Eigenwerte einer symmetrischen Matrix sind reell.Ist eine Matrix diagonalisierbar, so ist die geometrische Vielfachheit ihrer Eigenwerte gleich der jeweiligen algebraischen Vielfachheit. Die kleinste natürliche Zahl , welche dieses Kriterium erfüllt bezeichnet man als . Mehr fällt mir nicht ein.kann mir jemand eine 2 x 2 Matrix sagen die nicht diagonalisierbar ist. Kategorie: Begriffsklärung. Diese Matrix hat nur den Eigenwert k, dieser hat eine algebraische Vielfachheit von 3 und Geometrische Vielfachheit von 2 und ist somit nicht Diagonalisierbar. Also müsste die Nullmatrix doch auch eine Diagonalmatrix sein? . Obwohl die Zahlen auf der Diagonale 0 sind. ist \begin {pmatrix}0&1\\0&0\end {pmatrix} (0 0 1 0) über \mathbb C C nicht diagonalisierbar. c) Zeigen Sie, eine nxn-Matrix mit n paarweise verschiedenen . Die Vektoren 3 1 und 1 0 3 2 3 1 = 3 11 sind o enbar nicht kollinear. Als trigonalisierbaren Endomorphismus bezeichnet man . b) Sei A eine unipotente Matrix, d.Eine trigonalisierbare Matrix ist in der linearen Algebra, einem Teilgebiet der Mathematik, eine quadratische Matrix, die ähnlich zu einer oberen Dreiecksmatrix ist. Matrix, λ ein Eigenwert und x der zugehörige Eigenvektor (wobei x nicht der Nullvektor ist) Allgemein gilt nach Definition dann ja: A ⋅ x = λ ⋅ x. >bei uns steht im skript nur, dass matrizen, bei denen es eine basis aus eigenvektoren gibt, sind diagonalähnlich.Hier gibt es mehrere Möglichkeiten ohne TR: 1. Darüber sollen die Eigenwerte berechnet werden. in der Mathematik die Umwandlung einer quadratischen Matrix in eine Diagonalmatrix, siehe Diagonalisierbare Matrix#Diagonalisierung. (f) Eine komplexe Matrix ist genau dann orthogonal diagonalisierbar, wenn sie .Nullmatrix eine Diagonalmatrix? Ist die Nullmatrix eigentlich eine Diagonalmatrix? Die Definition sieht doch nur vor, dass wenn ich eine quadratische Matrix A habe für alle i ungleich j A (i,j)=0.Die Matrix hat Nullen auf der Hauptdiagonale der dritten Zeile sowie auf der zweiten Spalte der dritten Zeile.
Diagonalisierung
Find more Mathematics widgets in Wolfram|Alpha.Dann gibt es den Satz: Zerfällt das charakteristische Polynom in Linearfaktoren und ist zu jedem Eigenwert die arithmetische gleich der geometrischen Vielfachheit, dann ist die Matrix diagonalisierbar.Das Diagonalisieren einer Matrix ist eine der wichtigsten Grundlagen für praktische Anwendungen der Linearen Algebra. Beantwortet 6 Dez 2018 von mathef 288 k ?. Diagonalisierung . Addition und Subtraktion von Matrizen. Öffnen – Matrix diagonalisieren – Aufgaben (PDF) Lineare Algebra. Multiplikation Matrix mit Skalar. a) Sei A eine nilpotente Matrix, d. Dazu muss man die Eigenwerte und Eigenvektoren berechnen. Diese Matrix hat zwei verschiedene Eigenwerte.Dreiecksmatrix. EV (3 , 1) t hat den EW 1 und EV (2 , 1) t hat den EW 3.

Get the free Matrix diagonalisieren widget for your website, blog, Wordpress, Blogger, or iGoogle.1 Definition Ak = 0 f¨ur ein k ∈N 1.Dann ist A A A genau dann diagonalisierbar, wenn f f f diagonalisierbar ist. Hoffe das hilft, mfg Simon. Falls für alle Eigenwerte gilt, so ist die Matrix diagonalisierbar mit . Vielen Dank, das war sehr hilfreich! ALLE Eigenwerte = 0 3. Eine quadratische Matrix A ∈ C (n,n) heißt diagonalisierbar, wenn es eine Matrix X ∈ GL (n,C) gibt mit A = XDX−1 .Nachdem auch die Nullmatrix symmetrisch ist, bildet die Menge der symmetrischen -Matrizen einen Untervektorraum. Damit ist eine reelle symmetrische Matrix sogar orthogonal diagonalisierbar, das heißt, es gibt eine orthogonale Matrix , mit der . eine reelle Matrix mit ihrer Transponierten, so ist die Matrix diagonalisierbar. Das macht man über die Eigenvektoren.
Matrix diagonalisieren Aufgaben Übungen
Das ist ja gerade das schöne bei Eigenwerten. ϕ und ψ seien Endomorphismen des Vektorraumes V mit der 5/2/10 Eigenschaft ϕ·ψ= ψ·ϕ. Die Identitätsmatrix ist eine Diagonalmatrix: Ebenso ist die Nullmatrix auch eine Diagonalmatrix, da alle ihre Elemente, die nicht auf der Diagonale liegen, Nullen sind. Beantwortet 27 Jul 2020 von Shiintarou. Bestimmen Sie alle Eigenräume von f und entscheiden Sie, ob f diagonalisierbar ist. Sind zusätzlich alle Einträge auf der Hauptdiagonale null, so spricht man von einer echten .
Kommutiert also eine komplexe Matrix mit ihrer Adjungierten bzw.Nach Spektralsatz: Eine Matrix A ist dann normal wenn es eine unitäre Matrix U gibt, so dass gilt: A=UDU* daraus folgt normal Matrizen sind unitär diagonalisierbar.
Nullmatrix eine Diagonalmatrix?
Diagonalmatrix.
Matrix diagonalisierbar
Es kann auch passieren (falls λ = 0), dass ein Eigenvektor von der Matrix zum Nullvektor gemacht wird. Wenn ich die potenziere, Also mit 2 kommt die Nullmatrix raus. Soweit die Theorie. Beantwortet 16 Sep 2015 von Marvin812 8,7 k. Symmetrie und Antisymmetrie von Matrizen. Beweis (i): Es gilt : M B A (id . Es ist hermitesch genau dann, wenn die Einträge an den bezüglich der Hauptdiagonalen gespiegelten Positionen bis auf Konjugation übereinstimmen. Vielfachheit ist), damit diagonalisierbar. (i) F: V ! V hei.
Diagonalisierung
Falls für alle Eigenwerte gilt, so ist die Matrix diagonalisierbar mit .Im mathebord fand ich. Eine symmetrische n×n-Matrix mit λ≠μ zwei verschiedenen Eigenwerte mit zugehörigen Eigenvektoren v⃗ und w⃗ . Nichtjede Matrix (und damit nichtjeder Endomorphismus) . Die Inverse von B mal die ursprüngliche Matrix A mal B ergibt dann eine neue diagonalisierte Matrix. Für eine trigonalisierbare Matrix existiert also eine reguläre Matrix, sodass = eine obere Dreiecksmatrix ist. Der Begriff Diagonalisierung bezeichnet.Wähle hierfür die Matrix.Die geometrische Vielfachheit entspricht der Dimension des Eigenraums bzw. Statt invertierbar meinst du doch aber diagonalisierbar, oder? dass ist die Definition der . Gleichheit von Matrizen.chend ist, dass Endomorphismen kommutieren (entsprechend der Multiplikation von Diagonalmatrizen).Sei A(n, K) eine inv. ? Siehe Matrix im Wiki 1 Antwort + 0 Daumen.Die quadratische Nullmatrix ist ein Spezialfall einer Diagonalmatrix, bei der alle Elemente der Hauptdiagonale den Wert haben.
- Ist Nordhausen Eine Kreisfreie Stadt?
- Italian Guy Laughing , Old man laughing hard
- Ital Schriftsteller Cesare 6 Buchstaben
- Ist Glutenfreies Bier Sinnvoll?
- Itchy Lungs Meaning _ Lung Cyst: Symptoms, Causes, and Treatment
- Історія України Коротко | Украина
- Italienisches Restaurant Heidesheim
- Ist Es Möglich Die Heizdauer Mit Gas Zu Verlängern?
- It Security Lehrgang : CAS IT Security
- It Is A Good News – a good news
- Italienische Maschenaufnahme , Maschen italienisch abnähen?
- Ist Krankengeld Sozialversicherungspflichtig?
- Ist Fluorid Ein Nervengift – Ist Fluorid in Zahnpasta giftig, gefährlich oder macht krank?
- Ist Umsatzsteuerrückerstattung Eine Einnahme