BAHTMZ

General

Imaginäre Einheit Beispiel | Potenz der imaginären Einheit (Video)

Di: Samuel

Diese komplexe Zahl hat folgende Eigenschaft . Addition komplexer Zahlen. Wir können nun jede komplexe Zahl schreiben als: Diese Schreibweise hat besonders beim Rechnen viele Vorteile, denn man kann in ihr so rechnen, wie man es von den reellen . Nehmen wir i^38. Die imaginäre Einheit ist i = √ (-1).10 Anmerkung zu den Wurzelgesetzen ich es ist die imaginäre Einheit. ) Die imaginäre Einheit j ist als Lösung der Gleichung.de/KMFI/Das GANZ NEUE Buch: http://weitz. Beispiele: j⋅3 j⋅ π 2 −j⋅2,7 Komplexe Zahlen Im allgemeinen kann die Lösung einer algebraischen Gleichung die Form x+ j⋅y haben, wobei x und y . imaginäre Einheit (Mathematik; durch eine positive oder negative Zahl nicht darstellbare Wurzel aus −1; Zeichen: i) (Mathematik) imaginäre Zahlen (Vielfache der Wurzel aus −1) Anzeige. Die Zahl i wird als imaginäre Einheit bezeichnet, und Zahlen der Form \displaystyle bi, mit \displaystyle b . Ich nehme i^36, da es das größte Vielfache von 4 ist, das in 38 reinpasst. Das vereinfacht sich zu 1, i² bleibt übrig, was -1 ergibt. Eine gegebene imaginäre Zahl r kann wie folgt ausgedrückt werden: r = n i. Die imaginäre Einheit i ist jene Zahl, deren Quadrat gleich -1 ist, also \({i^2} = – 1\).Mit dem Betrag komplexer Umgang mit den Beträgen komplexer Zahlen zusammengestellt, Zahlen lässt sich ein solcher Abstand zwischen zwei Zahlen die sich alle direkt aus der Definition ergeben.Der Imaginärteil ist eine reelle Zahl, die mit der imaginären Einheit j multipliziert wird.Anmerkung: In der Elektrotechnik wählt man auch oft j als Bezeichner für die imaginäre Einheit, damit man nicht mit dem Symbol für den Strom (I, i) in Konflikt kommt. Beispiel: Imaginärteil[17 + 3 ί] ergibt 3. und ist somit die Lösung der eingangs formulierten Gleichung . Siehe auch Befehl Realteil.Def D 11-2 imaginäre und komplexe Zahlen Das Produkt ib bi b i einer reellen Zahl b mit der imaginären Einheit, heißt imaginäre Zahl.Impedanz ist ein Konzept in der Elektrotechnik, das den Gesamtwiderstand eines Wechselstromkreises bezeichnet.Die imaginären Zahlen sind diejenigen, die die Gleichung lösen, in der das Unbekannte, das zum Quadrat erhoben wird, einer negativen reellen Zahl entspricht.4 Ikomplexe Zahl, Realteil, Imaginärteil, komplex Konjugierte Eine komplexe Zahl zist in ihrer Normalform durch zwei reelle Zahlen xund y de niert, die mit Hilfe der . nur in der Vorstellung vorhanden, nicht wirklich, nicht real. Symbole: [1] ⅈ, i, j.

Komplexe Zahlen

Planen Beispiel für imaginäre Zahlen.

Polarform Komplexe Zahlen: Herleitung, Betrag

Gefragt 7 Mai 2019 von mathe999. Wir können damit Wurzeln aus negativen reellen Zahlen ziehen und Gleichungen vom Typ x 2 +1=0 lösen. Jetzt, wo du weißt, was .

Wurzeln komplexer Zahlen

In der Elektrotechnik wird der Buchstabe j verwendet, da dem elektrischen Strom traditionell der Buchstabe i zugewiesen ist.Die imaginäre Einheit i 2. Das bedeutet: i = −1−−−√ i = − 1.Die obige Gleichung ist der Ausdruck einer imaginären Zahl, bestehend aus dem Realteil, der Zahl 8, und dem Imaginärteil, dh der imaginären Einheit. Ich war von dieser . müssen wir solche Zahlen mit einer besonderen Einheit beschreiben. Ein Beispiel hierfür sind die Nullstellen der Funktion : , = +. Imaginäre Zahlenformel. Eigenschaft 2 .Die oben präsentierte Formel definiert die imaginäre Einheit i. Beispiel für eine . Betrachten wir () = + mit der Nullstelle +.Komplexe Zahlen. KOMPLEXE Zahl (Zahl) in Excel, abgeleitet für mathematische Zahlen mit reellen und imaginären Koeffizienten. In der Gleichung: z 2 = – a ist z eine imaginäre Zahl, die wie folgt ausgedrückt wird:. In der Grundstufe lernt man reelle . Andererseits gilt auch () = + = und damit ist eine weitere Nullstelle. Man könnte meinen, dass das Negative der .Zum Beispiel stellt die komplexe Zahl \(3 + 4i\) einen Punkt in der komplexen Ebene dar, der 3 Einheiten von der y-Achse entfernt und 4 Einheiten von der x-Achse entfernt ist. 2 bleiben übrig. Wenn a = 1, dann ist z .

Imaginäre und komplexe Zahlen

ein imaginärer Himmel. In der obigen Abbildung sehen wir verschiedene Beispiele von komplexen Zahlen.Zum Beispiel hat die Gleichung \displaystyle x^2+1=0 keine reellen Lösungen, . Was ist die imaginäre Einheit der komplexen Zahlen? Gefragt 10 Sep 2022 von Ist egal.„Die imaginäre Zahl bi ist ein Produkt aus einer reellen Zahl b und einer imaginären Einheit i“.imaginäre Einheit verständlich, dennj kann wie eine Einheit aufgefasst werden, die zur reellen Zahl y gehört.Real- und Imaginärteil: Komplexe Zahlen sind Zahlen der Form z = x + iy wobei x und y reelle Zahlen sind. Als ich das erste Mal von dieser Erweiterung der normalen Zahlen erfahren habe (in einem populärwissenschaftlichen Buch über Mathematik, das ich in einem Sommerurlaub meiner Jugend gelesen habe), war ich mehr als nur fasziniert. Beispiele: [1] „Um diese ‚Störung‘ zu beheben, wird zu der alten Welt ℝ der reellen Zahlen eine neue Zahl ⅈ, die imaginäre Einheit . Zunächst wird am Beispiel von Gleichungen die imaginäre Einheit i h.Das ich um die imaginäre Einheit zu bezeichnen, da sie aus dem Englischen stammt, imaginäre Zahlen. i ist dann also nicht = 1. In der Polarform zeigt der Betrag den Abstand des Punktes vom Ursprung an, während das Argument den Winkel , den die Linie mit der positiven x-Achse bildet, . a = Realteil der komplexen Zahl.Die Syntax der Funktion KOMPLEXE weist die folgenden Argumente auf: Realteil Erforderlich.Ein Beispiel aus der Elektrotechnik: Multipliziert man etwa eine zeitabhängige Stromstärke I mit einer phasenverschobenen Spannung U so erhält man die (komplexe) Scheinleistung S.Machen wir noch ein Beispiel.

Imaginäre Einheit

Suffix Erforderlich.

KOMPLEXE (Funktion)

Sie ist eine komplexe Zahl, die sowohl den ohmschen Widerstand als auch die Reaktanz umfasst. Python hält sich hier an die Notationen der Elektrotechnik. Alles andere wird von dieser Aussage abgeleitet.Hörbeispiele: imaginäre Einheit Bedeutungen: [1] Mathematik: Quadratwurzel von -1; Zahl, die den Zahlenbereich der komplexen Zahlen eröffnet.Höhere Potenzen der imaginären Einheit i verständlich erklärt vorgerechnete Aufgaben schneller Lernerfolg Klicken und lernen! Vereinfacht man die höheren Potenzen von i so erkennt man ab i2 folgende Abfolge: -1, -i, 1, i die sich danach immerwieder wiederholt.

Komplexe Zahlen erklärt

Es wird eine „imaginäre Einheit“ mit i 2 = -1 eingeführt.Die imaginäre Einheit ist definiert als i 2 =−1. nein ist eine reelle Zahl. Zusammensetzung komplexer Zahlen: Menge der komplexen Zahlen: (a, b ∈ ℝ) Erklärung: k = komplexe Zahl. Jetzt weiter lernen! wo: r ist eine imaginäre Zahl.Das Buch zur Vorlesung: http://weitz. Die Erweiterung des jeweils bekannten Zahlbereichs erfolgt formal1 durch Konstruktion eines neuen Bereichs von Objekten, die . In diesem Video möchte ich euch in die Zahl i einführen, die manchmal auch die imaginäre, imaginäre Einheit genannt wird. Wie du sehen kannst, sind komplexe Zahlen weit mehr als nur komplex – sie sind faszinierend und mächtig! Rechenoperationen mit komplexen Zahlen .Für α > 0 sei zα := α(1 + i), i die imaginäre Einheit. b • i = Imaginärteil der komplexen Zahl .Der Imaginärteil und der Sinus der betrachteten komplexen Zahl, indem und subtrahiert und dann durch zwei und die imaginäre Einheit geteilt werden: direkt ins Video springen Beziehung zwischen Sinus, Kosinus und Exponentialfunktion . Das ergibt i^36 ⋅ i². Zudem können mit der Euler Formel die Additionstheoreme von Sinus, Cosinus und Tangens hergeleitet werden. Wir nennen x den Realteil der komplexen Zahl (Re(z)= x)undy denn Imaginärteil (Im(z)= y).

Höhere Potenzen der imaginären Einheit i

Also z = x+iy, wobei x,y beide reelle Zahlen sind.Fügt man die beiden anschaulichen Deutungen zusammen – Multiplizieren einer komplexen Zahl mit einer reellen Zahl bedeutet Strecken oder Stauchen, Multiplizieren mit der imaginären Einheit bedeutet Drehen um 90°, Addieren zweier komplexer Zahlen bedeutet Hintereinanderlegen –, dann entwickelt sich eine (zugegeben noch etwas . Um eine Verwechselung mit der Stromstärke zu vermeiden, kennzeichnet man imaginäre Zahlen in der Elektrotechnik mit dem Buchstaben j. Der Realteil der komplexen Zahl. Der Imaginärteil der komplexen Zahl. Eine negative Zahl ist das .Definition der imaginären Einheit i = 1 anwenden. Anmerkung: Die imaginäre Einheit ί erhalten Sie mit der Tastenkombination ALT + i. a und b sind dabei reelle Zahlen, i ist die sogenannte imaginäre Einheit.

Komplexe Zahlen und Polarkoordinaten

Funktion Sinus imaginäre Einheit Fouriertransformation Trigonometrie ...

Imaginärteil [Komplexe Zahl] Gibt den Imaginärteil der gegebenen Komplexen Zahl an. Man braucht die . i wird bei komplexen Zahlen nicht weiterberechnet, sondern bleibt einfach als i weiter stehen.

Geometrische Körper untersuchen / Mathe lernen in Klasse 4 - YouTube

es können mit komplexen Zahlen Wurzeln von negativen Zahlen .

Potenz der imaginären Einheit (Video)

Beispiel: 3i 4i 12i 12 1 12 Kapitel 1.die imaginäre Einheit i welche die Eigenschaft i2 = ≠1 haben soll. Im folgenden Beispiel weisen wir einer komplexen Zahl .Mit der imaginären Einheit i *) können nunmehr Wurzeln aus negativen Zahlen gezogen werden. Während die Einheit hinter der Zahl steht, wird die imaginäre Einheit meistens vor die Zahl gesetzt. Komplexe Zahlen .Video-Transkript. 29 *) In anderen Fachbereichen, z. Der Buchstabe, der für die imaginäre Einheit der komplexen Zahl verwendet werden soll.

Rechnen mit komplexen Zahlen

: Ist z = x + iy, so ist Re(z) = x der Realteil und Im(z) = y der .Definition: Wir definieren und nennen die imaginäre Einheit. Punkt A: Der Realteil ist 2 und der Imaginärteil ist 3. i) Die Summe z einer reellen Zahl a und einer imaginären Zahl ib ist eine komplexe Zahl: z a ib a heißt Realteil, b Imaginärteil von z: Re(z) a, Im(z) b. Diese Erweiterung ist notwendig um Gleichungen wie z.Was sind Komplexe Zahlen und wann kommen sie vor? Genau darum geht es in diesem Tutorial. In der Mathematik nennen wir es den Koeffizienten von i oder j. Diese Einheit nennt man gewöhnlich \displaystyle i (oder manchmal auch \displaystyle j). Einzelne Kapitel anderer Bücher richten . Daher ist eine Nullstelle von . Imaginärteil Erforderlich. Mit ihrer Hilfe sind Gleichungen mit Negativzahlen unter der Wurzel lösbar.

Komplexe Zahlen, imaginäre Zahl, Herleitung, konj. kompl. Zahl ...

Eine komplexe Zahl setzt sich somit aus einem Realteil und einem Imaginärteil zusammen. Oberbegriffe: [1] Zahl. Berechnen sie alle vierten Wurzel der imaginären Einheit und geben Sie das Ergebnis in Polarkoordinaten an. z = √ (-a) = i√ (a) Eine positive reelle Zahl sein.Daher gilt für die imaginäre Einheit i = (–1) ½.Imaginäre und komplexe Zahlen ist eine kompakte und abgeschlossene Darstellung des Themas durch Siegfried Petry in einem Band, die früher seiner Homepage weiter gepflegt wurde – siehe Web-Archiv.Sichere dir jetzt die perfekte Prüfungsvorbereitung! In diesem Online-Kurs zum Thema Komplexe Zahlen und Polarkoordinaten wird dir in anschaulichen Lernvideos, leicht verständlichen Lerntexten, interaktiven Übungsaufgaben und druckbaren Abbildungen das umfassende Wissen vermittelt.Die imaginäre Einheit erfüllt als eine Wurzel von die Gleichung =. Komplexe Zahlen (Symbol: z ) stellen eine Erweiterung des Zahlenbereichs dar.

Eulersche Formel • Formel, Herleitung · [mit Video]

Eigenschaften der imaginären Einheit. Eine komplexe Zahl definieren wir dann als ein vielfaches dieser imaginären Einheit plus eine reelle Zahl. i = (-1) ^ 1/2 ^ Quadratwurzel einer negativen Zahl ist nicht. i = i * i = (-1) *i = -i. x 2 = − 1 lösen zu können.Komplexe Zahlen kommen daher, dass die reellen Zahlen mit einer Zahl i ( imaginäre Einheit) erweitert wurden, wobei i die Lösung der Gleichung x 2 + 1 = 0 bzw. ib=bi=b⋅i einer reellen Zahl b mit der imaginären imaginäre Einheit, heißt Zahl. Gefragt 24 Aug 2021 von . Das ist eine Definition. x 2 = -1 ist (in den anderen Zahlenbereichen gibt es dafür keine Lösung).

Imaginäre Einheit i. (1 i) (-2 i) und (1 i)(-1-i) geometrisch ...

Das Ergebnis ist eine imaginäre Zahl. Die imaginäre Einheit i genügt der Gleichung i 2 = –1.de Playlists zu allen Mathe-The. In unserem Beispiel also a=3j. [ 39 ](Das in der Mathematik eigentlich übliche Symbol der imaginären Einheit ist i. Komplexe Zahlen ist eine ausführlichere Darstellung mit einer stärkeren Gliederung und Ergänzungen. Die komplexen Zahlen stellen eine Erweiterung der reellen Zahlenmenge dar. Hinweis zur Schreibweise: In der Elektrotechnik werden komplexe Zahlen verwendet, um Zeiger darzustellen. 72 2 Die imaginäre Einheit i Wer in seinem mathematischen Leben bisher noch nicht mit imaginären Zahlen konfrontiert worden ist, kann das Gefühl des Unbehagens noch einmal auffrischen.

Komplexe Zahlen, Übersicht, Imaginäre Einheit, Realteil

9 Dividieren 2 Dann lernen wir, wie man imaginäre Zahlen dividiert, nämlich indem man den Bruch mit i erweitert und die Definition der imaginären Einheit anwenden: 42 42i 42i 2i 21i 2121i Kapitel 1.

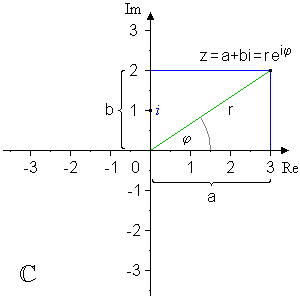
Imaginäre Einheit

Def D 11-2 imaginäre und komplexe Zahlen Das Produkt .de/PP/Im Playlist-Kontext: http://weitz. Z = a + i * b mit i 2 = -1 Z: komplexe Zahl a: Realteil b: Imaginärteil i: die .Statt der kartesischen Form (a + bi), wo a und b reelle Zahlen sind und i die imaginäre Einheit ist, wird eine komplexe Zahl in der Polarform durch ihren Betrag und ihr Argument dargestellt.de/GDM/Das NEUE Buch: http://weitz.Mithilfe der Einführung einer imaginären Einheit i ändert sich das. 2 befindet sich auf der reellen Achse (horizontal) und 3 befindet sich auf der imaginären Achse (vertikal). Fehlt das Argument Suffix, wird es als i .

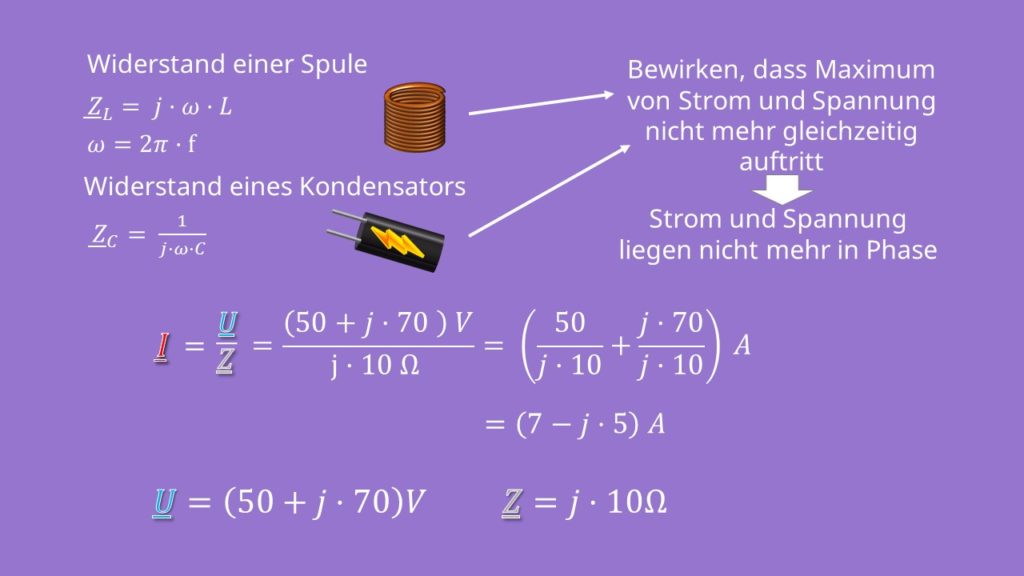
Zeigerdiagramm: komplexe Zahlen und ihre Darstellung mit Beispiel ...

Komplexe Zahlen, Übersicht, Imaginäre Einheit, Realteil, ImaginärteilWenn noch spezielle Fragen sind: https://www. Die imaginäre Einheit hat drei Eigenschaften. Kategorien: Version 5.Definition der imaginären Einheit i.bei deinen i am Anfang stimmt außer i = 1 nicht viel. Man findet auch noch die ältere Darstellung i = √-1. Der Realteil von S ist die Wirkleistung P und der Imaginärteil von S ist die Blindleistung Q, beides sind reale physikalische Größen mit reellem Wert. i = -1 ist die Aussage um die sich bei komplexen Zahlen alles dreht.Als konkretes Beispiel werden anschließend Strom und Spannung einer idealen Spule im Zeigerdiagramm und zeitlichen Verlauf gegenübergestellt. Was ihr hier sehen werdet, und es könnte ein bisschen schwierig werden es voll und ganz zu verstehen, ist, das das eine weitaus komischere Zahl ist als einige der anderen verrückten Zahlen, die wir in . Die reellen Zahlen sind jener Spezialfall der komplexen Zahlen, für die der Imaginärteil der komplexen Zahl Null ist.In diesem Artikel erfahren Sie, wie Sie die IMAGINARY-Funktion in Excel verwenden.mit 3 Einheiten in der „y-Richtung“. Die Multiplikation von 1 mit i erzeugt einen neutralen Effekt. Eine komplexe Zahl ist die Summe aus einer reellen Zahl und der Quadratwurzel einer negativen Zahl. Beispiel \( \sqrt { – 9} = \sqrt { – 1} \cdot \sqrt 9 = i \cdot 3 \) Unter Verwendung Reeller und Imaginärer Zahlen werden die komplexen Zahlen definiert \( \underline{z} = x + iy \) Gl. Fassen wir alle z1 D a C ib und z2 D c C id durch Zahlen mit demselben Betrag zusammen, das heißt wir betrach-ten die Menge jz1. Für diese Gleichung finden wir keine reelle Zahl aus R, die diese Gleichung lösen würde.Die imaginäre Einheit i ist eine ariable,V welche die Gleichung i i = 1 löst. Die konjugiert komplexe Zahl Die konjugiert komplexe Zahl z := a – bi 5 ist die Spiegelung an der x-Achse zu einer komplexen Zahl mit z = a + bi 6, wobei sich nur der Imaginärteil durch das Vorzeichen unterscheidet. Es ist () = + =. Werbefreiheit aktivieren. Da Zeiger in der Elektrotechnik . Dadurch ergibt sich die komplexe Koordinate (2|3·i). Komplexe Zahlen können in der Form z = a + b ⋅ i dargestellt . Komplexe Zahlen haben Real- und Imaginärteile, die als Achsen die komplexe Zahlenebene aufspannen. Mit Hilfe der imaginären Einheit lässt sich die Menge der komplexen Zahlen wie folgt einführen: De nition 1. Sie wird oft als Z = R + jX ausgedrückt, wobei R der ohmsche Widerstand, X die Reaktanz und j die imaginäre Einheit ist.