How To Interpret Regression Equation

Di: Samuel

A simple linear regression model takes the following form: ŷ = β0 + β1(x) where: ŷ: The predicted value for the response variable. If you saw only the equations, you’d think the models are very similar. That is a great result. How to Read and Interpret a Regression Table Understanding the Null Hypothesis for Linear Regression Understanding the F-Test of Overall Significance in Regression.The general form of the linear model for country i (Image by Author) In the above equation: y_i is a matrix of size [T x 1] containing the T observations for country i. It is often warranted and a good idea to use logarithmic variables in regression analyses, when the data is continous biut skewed.A regression equation is used in statistics to find out what relationship, if any, exists between data sets.Interpreting regression analysis 1 Workshop overview • Welcome • What this workshop is not • a “ﬁrst course” in statistics for those who desire a fundamental under-standing of what to do, or not do. When we assume some characteristics (e.5, which sits in front of the variable . A random sample of 11 .

PPT - Logistic Regression PowerPoint Presentation, free download - ID ...

These two regression equations are almost exactly equal. The column of estimates (coefficients or parameter estimates, from here on labeled coefficients) provides the values for b0, b1, b2, b3 and b4 for this equation.

Regression Tutorial with Analysis Examples

While interpreting the p-values in linear regression analysis in statistics, the p-value of each term decides the coefficient which if zero becomes a null hypothesis.estimated regression equation, in statistics, an equation constructed to model the relationship between dependent and independent variables. log(Y) = β0 + β1 log(X) A 1% increase in X is associated with an average change of β1% in Y. Usually, you must be satisfied with rough predictions. In the above equation, it can be seen that the bias introduced in the estimated value β_cap_i is directly proportional to the covariance between the omitted variable z_i and the explanatory variables X_i. For example, if you measure the height of a child each year you might find that it grows about 3 inches a year. Step 2: Find the y -intercept. A low p-value of less than . So the (average) difference in pay between men and women is then LnWmen – LnWwomen.The sums of squares are reported in the Analysis of Variance (ANOVA) table (Figure 4). This could mean that if a predictor has a low p-value, it could be an effective addition to the model as . P value for b3 would indicate whether the correlation is significant.Interpret the meaning of the slope of the least squares regression line in the context of the problem. This will fit a curved line to the data and will show you . Share 0 Facebook Twitter Pinterest Email.

Interpreting slope of regression line (video)

Y = β0 + β1X.Although I am a little offended by a RTFM (but maybe that’s just me): The problem is that in all I’ve read, at least with regard to doing linear regression in R, people sometimes do this, others do that. We see that the adjusted R-squared is 0.Categorical variables (also known as factor or qualitative variables) are variables that classify observations into groups.1955 when mpg goes up by one, and is predicted to be 11905.The formula for regression with a moderator is.1) By testing this model, three possible coefficients and p values would be given. Learning Outcomes.0564)-1) \cdot 100 = 5. In this case, adding a quadratic term to the regression equation may help model the relationship between X and Y. It doesn’t occur to me why one would use this for regression if the .In the Data Frame window, you should see an X (index) column and columns listing the data .Linear regression analysis is based on six fundamental assumptions: The dependent and independent variables show a linear relationship between the slope and the intercept. Residuals, also called “errors .Interpreting results Using the formula Y = mX + b: The linear regression interpretation of the slope coefficient, m, is, The estimated change in Y for a 1-unit increase of X.96 percentage points fall though). gender and age category, with three levels for age) and are looking at how they pertain to some continuous measure (our dependent variable, e.The regression equation is presented in many different ways, for example: Ypredicted = b0 + b1*x1 + b2*x2 + b3*x3 + b4*x4.

How to Interpret Regression Analysis Results: P-values

In other words, the slope of a line is the change in the y variable over . Y=b1X1+b2X2+b3X1X2+C (5. R-squared is always between 0 and 100%: 0% represents a model that does not explain any of the variation in the response variable around its mean.An interaction effect occurs when the effect of one variable depends on the value of another variable. There are several ways to find a regression line, but usually the least-squares regression line is used because it creates a uniform line. Recall from the beginning of the Lesson what the slope of a line means algebraically. Prior to running the model I have normalized the dependent variable Y and the independent variables X1 and X2.Interpreting the Intercept in Simple Linear Regression. The fact that regression analysis is great for explanatory analysis and often good enough for prediction is rare among modeling techniques. Finally, we fit a linear-log function to the data by entering the following equation into Demos’ command line: y 1 ∼ b + m ln ⁡ (x 1) y_{1}\sim b+m\ln(x_{1}) y 1 ∼ b + m ln (x 1 ). m = change in y change in x.Linear regression models are known for being easy to interpret thanks to the applications of the model equation, both for understanding the underlying relationship and in applying the model to predictions. Do I use the absolute value then turn it into a negative like this: $(\exp(0. β1: The average change in the response variable for a one unit increase in x. Once we have the estimates for the slope and intercept, we need to interpret them. Frankly, I do not understand the Wikipedia entry on orthogonal polynomials.44028 is needed to form a regression equation. Example: Interpreting R² A simple linear regression that predicts students’ exam scores (dependent variable) from their study time (independent variable) has an R² of . The mean of the dependent variable predicts the dependent variable as well as the regression model.292 (foreign) + 11905. The value of the residual (error) is zero. If you extend the regression line downwards until you reach the point where it crosses the y-axis, you’ll find that the y-intercept value is negative! In fact, the regression equation shows us that the negative intercept is -114. This line goes through ( 0, 40) and ( 10, 35) , so the slope is 35 − 40 10 − 0 = − 1 2 . If this, however, is correct, why do the results change? Is this just the .

Curve Fitting using Linear and Nonlinear Regression

But this works the same way for interpreting coefficients from any regression model without interactions.data), and an Import Dataset window pops up.R-squared is the percentage of the dependent variable variation that a linear model explains.A regression coefficient is the quantity that sits in front of an independent variable in your regression equation.So in the case of a regression model with log wages as the dependent variable, LnW = b 0 + b 1Age + b 2Male the average of the fitted values equals the average of log wages Yˆ =Y _) _ ^ Ln(W =LnW. The value of the residual (error) is constant across all observations.In regression analysis, curve fitting is the process of specifying the model that provides the best fit to the specific curves in your dataset.2 – Interpreting the Coefficients. So the (average) difference in pay between men and women is . The equation becomes: Y = β0 + β1X + β2X2 Y = β 0 + β 1 X + β 2 X 2. Step 3: Write the equation in y = m x + b form. Use the regression equation to predict its retail value.

interpretation

It is easiest to think about interactions in terms of discrete variables. We can see that the line passes through ( 0, 40) , so the y -intercept is 40 . If the slope is denoted as m, then. Perhaps you might have studied two-way ANOVAs, where we have two grouping variables (e.15, I know that it means that for addition of one standard . A linear regression model with two predictor variables results in the following equation: Y i = B 0 + B 1 *X 1i + B 2 *X 2i + e i., time or geolocation).

The Regression Equation

Even if your regression model is significant, there are some additional considerations to keep in mind when interpreting the results of simple linear regression analysis: Linear regression doesn’t prove causation : a statistically significant regression model doesn’t prove that a cause-and-effect relationship exists between two variables. by Marco Taboga, PhD. Fixed effect regression, by name, suggesting something is held fixed. Either a simple or multiple regression model is initially posed as a hypothesis concerning the relationship among the dependent and independent variables. Typically, you have a set of data whose scatter plot appears to “fit” a straight line.

The Complete Guide: How to Report Regression Results

42 – telling you that price is predicted to increase 1767. In this post, I explain interaction effects, the interaction effect test, how to interpret interaction models, and describe the problems you can face if you . The p value of the F-statistic is . Here is a table that shows the correct interpretation for four different scenarios: Dependent. Here is a breakdown of the components of the regression question:In short, interaction terms enable you to examine whether the .

How to Perform Simple Linear Regression in Stata

Step 1: Find the slope.80$ or

Simple Linear Regression in SPSS, Including Interpretation

For linear relationships, as you increase the independent variable by one unit, the mean .; Choose the data file you have downloaded (income.

Linear Regression in R

For example, if the coefficient of X1 is 0.This tells us the average value of the response variable when the explanatory variable is zero.

PPT - Introduction to Multiple Regression PowerPoint Presentation, free ...

Video ansehen2:58Jonathan Veersma.A 1 unit increase in X is associated with an average change of 100×β1% in Y.The alternative hypothesis is: Conceptual H 1: Cultural Intelligence will predict Sustainable Innovation Behavior. The first portion of results contains the best fit values of the slope and Y-intercept terms.; X_i is a matrix of size [T x k] containing the values of k regression variables all of which are observable and relevant. The slope of a least squares regression can be calculated by m = r (SDy/SDx)., user characteristics, let’s be naive here) are constant over some variables (e.

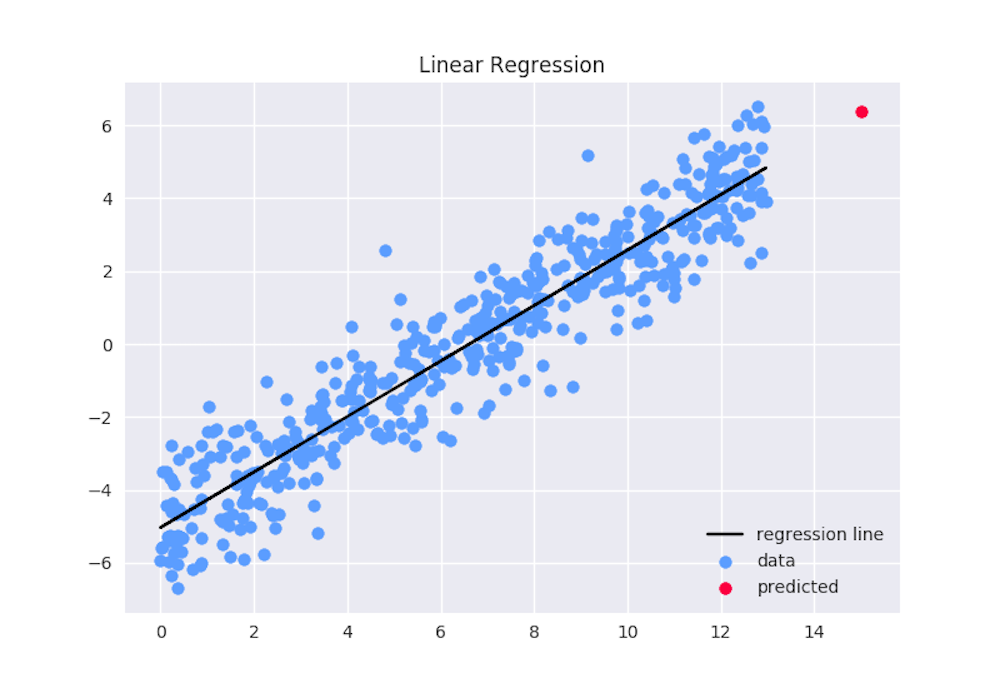
The linear regression equation example - topvia

Curved relationships between variables are not as straightforward to fit and interpret as linear relationships. β0: The mean value of the response variable when x = 0. Now consider that the R-squared for the Output1 model is 14.I have a linear regression model where the dependent variable is logged and an independent variable is linear. Then, b1 and b2 is the coefficient for direct effect while B3 is the interaction.The p-value is used to test the hypothesis that there is no relationship between the predictor and the response. previous post .The Regression Equation. After receiving the output I want to interpret the results.

Why Add & How to Interpret a Quadratic Term in Regression

Next, we will explain where each of these interpretations comes from. I have data containing several variables.Actually, after pondering about this for a while, I would interpret the second regression just the same (now resulting in a 0.For this post, I modified the y-axis scale to illustrate the y-intercept, but the overall results haven’t changed. A variable is standardized by subtracting from it its sample mean and by dividing it by its standard deviation. Note that the quadratic model does not . So a score difference of 15 (dy) would be divided by a .42 when both mpg and foreign are zero.Linear regression is a powerful statistical tool used to model the relationship between a dependent variable and one or more independent variables (features).Omitted variable bias: The bias introduced in the estimate of β_i due to the omission of the variable z_i (Image by Author). In fact, most things in the real .Linear regression with standardized variables.1955 (mpg) + 1767.Interpreting Regression Coefficients for Different Logarithmic Regressions In a simple linear regression, . In this example, the average mpg is 39.After being standardized, the variable has zero mean . The independent variable is not random.

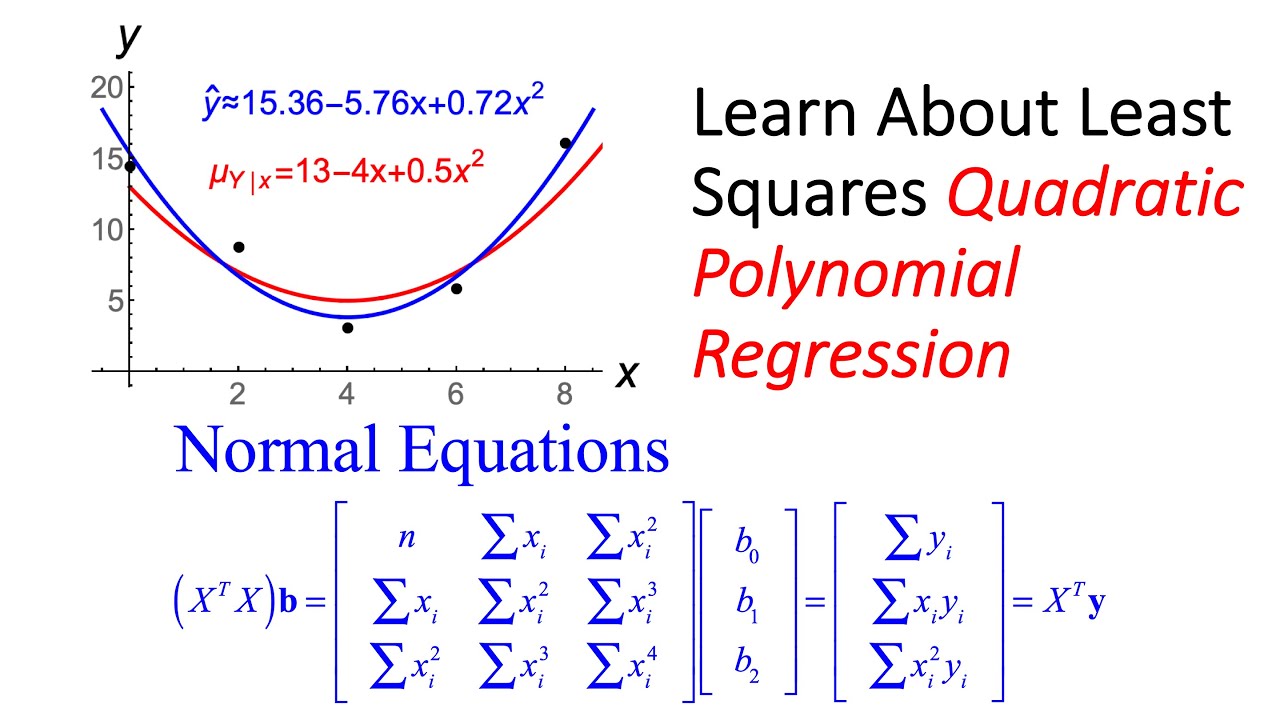
Regression Practical Meaning, Quadratic Polynomial Regression (Normal ...

They have a limited number of different values, called levels.

What Is Linear Regression In Machine Learning - Design Talk

This suggests a .Write a linear equation to describe the given model.

A Guide To Using The Difference-In-Differences Regression Model

Be careful: the R² on its own can’t tell you anything about causation. The slope coefficient for a key independent variable is negative: $-. The models aren’t as similar as they first appear. Let’s see what . 71% of the variance in students’ exam scores is predicted by .292 when the foreign variable goes up by one, decrease by 294. This tutorial covers many facets of regression analysis including selecting the correct type of regression analysis, specifying the best model, interpreting the results, assessing the fit of the model, generating predictions, and checking the assumptions.My tutorial helps you go through the regression content in a systematic and logical order. It is a parameter estimate describing the relationship between one of the independent variables in your model and the dependent variable. Linear Regression Equation. This doesn’t actually make much sense to interpret since the weight of a car can’t be zero, but the number 39. We assume regression analysis is the appropriate tool for your problems and you’ve seen it before • a detailed review, development or extension of what is . In this case (where the line is given) you can find the slope by dividing delta y by delta x. Create and interpret a line of best fit; Data rarely fit a straight line exactly.

How To Interpret R-squared in Regression Analysis

Step 1: Load the data into R.7% and for Output2 it is 86. The variables in the model are: Y, the response variable;

The No-Nonsense Guide to the Random Effects Regression Model

Suppose a four-year-old automobile of this make and model is selected at random. Follow these four steps for each dataset: In RStudio, go to File > Import dataset > From Text (base).A regression line, or a line of best fit, can be drawn on a scatter plot and used to predict outcomes for the $x$ and $y$ variables in a given data set or sample data.Training output of the Difference-In-Differences regression model (Image by Author) How to interpret the training output of the DID model. Regression analysis requires numerical variables. Suppose a $20$-year-old automobile of this make and model is selected at random.

Interpreting Regression Output

In the context of regression, the p-value reported in this table (Prob > F) gives us an overall test for the significance of our model. This lecture deals with standardized linear regressions, that is, regression models in which the variables are standardized. Not sure how to interpret.

How do I interpret my regression with first differenced variables?

In the Stata regression shown below, the prediction equation is price = -294. For example the gender of individuals are a categorical variable that can take two levels: Male or Female.The fitted regression model was: [fitted regression equation] . ² value, we know that:. Interaction effects are common in regression models, ANOVA, and designed experiments.How to interpret the coefficient of the dummy variable in the regression model Recollect that we had left out the dummy variable aspiration_turbo from the model to avoid perfect collinearity. Mathematical H 1: b ≠ 0. The least squares method is the most widely . Is this interpretation correct? It just feels weird that I transform my variables, but don’t have to change my interpretation.

A Comprehensive Guide to Interaction Terms in Linear Regression

This trend (which grows by three inches per year) can be modeled using a regression equation. An important, and often forgotten, concept in regression analysis is that of interaction terms. In the simple linear regression below, the quantity 0.Before we are going into explaining how the fixed effect model work, let’s introduce two terminologies.

Simple Linear Regression Derivation of OLS Estimators - YouTube

I ran a regression model.

PPT - Multiple Linear Regression and Correlation Analysis PowerPoint ...

The interpretation of the intercept parameter, b, is, The estimated value of Y when X equals 0.; β_i is a matrix of size [k x 1] containing the population .The example here is a linear regression model.05 allows you to reject the null hypothesis. How to Calculate the Sum by Group in .44028 when the weight of a car is zero. Graphs can really bring the differences to life. The model has been able to explain more than 50% of the variance in the response variable HPI_CHG. But it is imporant to interpret the coefficients in the right way. Expressed in terms of the variables used in this example, the . For a linear regression model without transformations. By leaving out aspiration_turbo , we have given the job of storing the mean price of the turbos to the regression model’s intercept.

Lecture 13 Use and Interpretation of Dummy Variables

Sustainable Innovative Behavior′ = ( b x Cultural Intelligence) + a.If this assumption is not met, linear regression will be a poor fit to the data (as shown in the figure below). This is called a Line of Best Fit or Least-Squares Line.

BAHTMZ

General