How To Find Ellipse In Coordinates
Di: Samuel
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
Equations of Ellipses
θ is equally divided into four symmetrical regions hence, the area of ellipse in Cartesian coordinates is given as. First we will learn to derive the equations of ellipses, and then we will learn how to write the equations of ellipses in standard form. = 4∫a 0 y dx = 4 ∫ 0 a y d x.
Ellipse Standard Form Calculator
I have a coordinate system to make that.
Elliptic coordinate system
To help you calculate the standard equation of an ellipse from its vertices and co-vertices, here’s our ellipse standard form calculator. (-6,-4)), which would be the resulting values of Canvas.Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteSince all 5 points lie on the same ellipse, the above linear equations must have common solution.compute p = D*n (ie solve n = inv(D)*p for p) But we need to scale this point so it is on the ellipse; a little algebra shows the appropriate point p is. θ or dx = −a sin θ dθ d x = − a sin. Later we will use what we learn to . The focus points for the ellipse are at F 1 and F 2.I am creating a bubbles game, that there is a lot of bubbles on the screen moving and i want to pop a bubble when i click on it with mouse. The formula generally associated . Does anyone know which commands/functions I can use to do this? Most of what I have .Substitute these into the equations for y2 and x2 and you come up with the following equations.To work with horizontal and vertical ellipses in the coordinate plane, we consider two cases: those that are centered at the origin and those that are centered at a point other than the origin. I’ve found a few other questions ( 1, 2) regarding the fitting of an ellipse to a set of data points and they all use the same piece of code from here. Full lesson on what makes a shape an ellipse here .
![(Bài 196)[Toán-Vật lý] Phương trình tiếp tuyến của hình Ellipse ...](https://i.ytimg.com/vi/vOUERfNhkz4/maxresdefault.jpg)
The foci (plural for focus) are two points inside the ellipse. ∫2π 0 r2 2 dθ ∫ 0 2 π r 2 2 d θ . Furthermore, I can actually identify . When a line segment is drawn joining the two focus points, then the mid-point of this line is the center of the ellipse. On your computer, open Google Maps . When given an equation for an .Is there an equation in cylindrical coordinates for an ellipse (tilted at some angle) on the surface of a right circular cylinder of radius r? For simplicity, I envision the cylinder to be coincident with the x-axis. Now changing in Polar-coordinates by setting y = b sin θ y = b sin. The two foci and are generally taken to be fixed at and , respectively, on the -axis of the Cartesian coordinate system .
Ellipse
It uses the ellipse standard form equation to find the center and vertices of an ellipse or acts as the calculator for writing the equation of the ellipse in standard form. Update: After thinking about this a . For a ellipse with a focus at (0,0), the ellipse’s equation in polar coordinate can be written as the following: Given ? = semi-major axis, ? = eccentricity, the other focus at the angle ?, Now, we can use the data points (??,??) to fit the equation above by non-linear least square method (ex: Levenberg–Marquardt . You can find your latitude and longitude in decimal format at the top. The endpoints of this axis are called the vertices of the ellipse. If \(a>b\) then the ellipse is wider than it is tall and is considered to be a horizontal ellipse. ∫π 2θ = 0∫ ab √b2cos2θ + a2sin2θr = 0 . is the polar equation of an ellipse with semiaxes a a, and b b, with the origin as one of the foci.
Set up double integral of ellipse in polar coordinates?
Next, you can try to use the reflective properties of an ellipse.

The equation of an ellipse is: $$ ax^2+by^2+cxy+dx+ey+f=0 $$ Hence you need $5$ points to obtain the coefficients: $(a,b,c,d,e,f)$, assuming that the center is unknown. Let’s suppose that 2 “nails“ are driven into a board at points F 1 and F 2, and suppose that the ends of a string of length 2a is attached to the board at points F 1 and F 2.
WPF Center Ellipse at X, Y
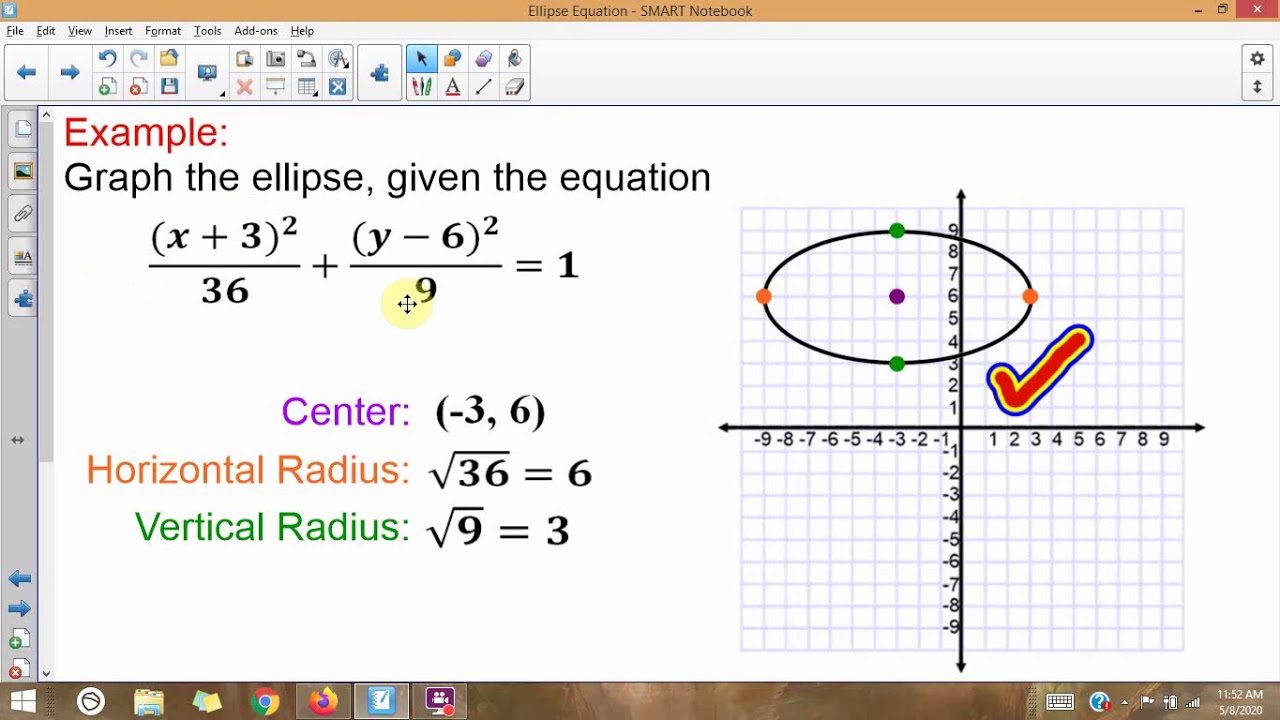
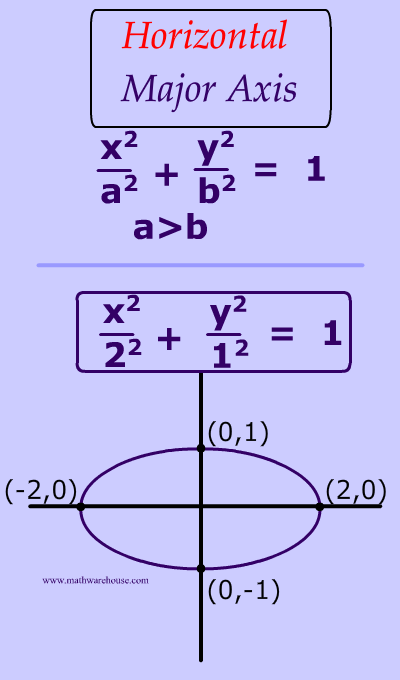
Video ansehen13:4911 years ago. First, verify that.To graph an ellipse, mark points \(a\) units left and right from the center and points \(b\) units up and down from the center. What I need is to calculate all the other possible points in the ellipse, as to know what other points the dot can be if it orbits the ellipse. Then the area of the ellipse in the first quadrant is the sum of all such elementary areas. In sewing, finding the vertices of the ellipse can be helpful for designing elliptic cutouts. Example : For the given ellipses, find the .I have the bounds of an ellipse in x- and y-coordinates. The following article will also share . If possible, I would also like to color in the specified ellipse on a 2d plot. The fixed points are known as the foci (singular . y = ± absinθ √(bcosθ)2 + (asinθ)2, x = ± abcosθ √(bcosθ)2 + (asinθ)2. I think there is a mistake in the code. You can rotate to make it a 2d problem if needed.Ellipses in Polar Coordinates. We can find the area of an ellipse calculator to .Video ansehen31:39This algebra video tutorial explains how to write the equation of an ellipse in standard form as well as how to graph the ellipse when in standard form. The coordinates of foci are (ae, 0) and (-ae, 0) (ii) For the ellipse x 2 a 2 + y 2 b 2 = 1, a < b. Alternatively you can in most cases project it onto the xy plane. For the points at minimum/maximum x, we start with n = (1,0) answered May 5, 2021 at 18:42.To transform it into polar coordinates,substitute (x, y) = (rcosθ, rsinθ) to get r = ab √b2cos2θ + a2sin2θ.
How to find the point on ellipse given the angle
e, the locus of points whose distances from a fixed point and straight line are in constant ratio ‘e’ which is less than 1, is called an ellipse.Autor: Sal Khan
Calculate Ellipse From Points?
From this, we see that the equation of the ellipse is given by setting the determinant of the matrix of coefficients of the above 6 equations to $0$. substitute x = 8.
Here is Roman’s suggestion implemented. If, on the the other hand, the center is known then $3$ points are enough, since every point’s reflection in respect to the center is also a point of the ellipse and you . These fixed points are called foci of the ellipse.

You now know another formula to find the coordinates of a point on an ellipse given only an angle from the center, or to determine whether a point is inside an ellipse .An ellipse is the set of all points[latex]\,\left(x,y\right)\,[/latex]in a plane such that the sum of their distances from two fixed points is a constant.If it is greater than 1, then the point is outside the ellipse. But if you want to determine the foci you can use the lengths of the major and minor axes to find its coordinates. Two points, A and B, are on the ellipse shown above.Mathematically, an ellipse is a 2D closed curve where the sum of the distances between any point on it and two fixed points, called the focus points (foci for plural) is the same. p = D*n / sqrt( n’*D*n) The point at minimum y is -p.
r = b2 a − a2 −b2− −−−−−√ cos t r = b 2 a − a 2 − b 2 cos t.
Foci of Ellipse Formula and Coordinates
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 2, which is 1 2.$\begingroup$ @draks: the arclength of an ellipse requires an elliptic integral of the second kind for representation. You might want to try following through on GEdgar’s suggestion.An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r_1 and r_2 from two fixed points F_1 and F_2 (the foci) separated by a distance of 2c is a given positive constant 2a (Hilbert and Cohn-Vossen 1999, p. Take an elementary area rdrdθ inside the ellipse. Later we will use . We explain this fully here. I am aware that the cylinder could be unwrapped into a plane, which would result in the ellipse becoming a sine curve. To copy the coordinates automatically, left click on the latitude and longitude. These two fixed points are the foci of the ellipse (Fig. In this situation, we just write “a ” and “b” in place of r. In doing the fitting: def fitEllipse(x,y): x = x[:,np. e have c = 6 c = 6, so: a2 = 36 +b2 a 2 = 36 + b 2 and the equation of the ellipse becomes: x2 36 +b2 + y2 b2 = 1 x 2 36 + b 2 + y 2 b 2 = 1. θ & x = a cos θ x = a cos.The vertices of an ellipse, the points where the axes of the ellipse intersect its circumference, must often be found in engineering and geometry problems. Each fixed point is called a focus (plural: foci). Formula for the focus of an Ellipse .7 and solve the equation for b2 b 2. The formula for finding the area of the ellipse is quite similar to the circle. If F1 and F2 are the foci, and the three points are P1, P2, and . The help for stat_ellipse says it uses a modified version of car::ellipse, so therefore I chose to extract the ellipse points from the ggplot object. When both foci are . Computer programmers also must know how to find the vertices to program graphic shapes.Elliptic coordinate system. The fixed point and fixed straight line are called focus and directrix respectively. The center will lie in that plane. If a actually an ellipse is determine by its foci.How find the equation of an ellipse for an area is simple and it is not a daunting task. First we will learn to derive the equations of ellipses, and then . The major axis is the line segment which passes through the foci of the ellipse. The orientation of an ellipse is determined by \(a\) and \(b\).Get the coordinates of a place. This will open a pop-up window.So you have only one free parameter in the equation that can be determined using the coordinates of the given point. The coordinates of foci are (0, be) and (0, -be) Also Read : Different Types of Ellipse Equations and Graph. Since an ellipse is the curve formed by all the points such that the sum of its distances from each of the two foci is constant, the foci are one of the main defining inputs for an ellipse, along with the constant distance sum. In my case, I already have the a/b parameters, so my ellipse is known shape, and I am basically trying to find the rigid body transformation to fit the ellipse at each frame. b sin t / (a cos t) = tan θ. First you can identify the plane containing the three points. If the string is pulled tight around a pencil’s tip, then the points P traced by the pencil as it moves within the string form an ellipse. I can get the position of Mouse easily but i don’t know how to get the position of the ellipse in order to check the intersection with the point of the mouse. Draw an ellipse through these points. In the above applet click ‚reset‘, and ‚hide details‘. t= arctan(a tan θ / b) + n * π. Below are the steps for the above approach: Calculate the value of theta using the formula: theta = atan2 (b * (y – k), a * (x – h)) Calculate the value of the distance from the formula mentioned above.I know the position of the red dot relative to the center, I have the vertical distance and the horizontal distance values. This results in the two-center bipolar coordinate equation r_1+r_2=2a, (1) where a is the . r = 8 2 − 3sinθ = 8(1 2) 2(1 2) − 3(1 2)sinθ r = 4 1 − 3 2sinθ. ax2 + by2 + cxy + dx + ey + f = 0 a x 2 + b y 2 + c x y + d x + e y + f = 0. The sum of the distances from A to the focus points is d 1 . I am just not sure . You can then use the formula.Autor: The Organic Chemistry Tutor In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae.In conic sections, a conic having its eccentricity less than 1 is called an ellipse.However, as @Sebastian points out, if you wish to compute the exact intersection with a line through the center with angle theta, it gets a bit more complicated, since we need to find a t that corresponds to theta: y(t)/x(t) = tan θ. (i) For the ellipse x 2 a 2 + y 2 b 2 = 1, a > b. The set of all points in a plane, the sum of whose distances from two fixed points in the plane is constant is an ellipse.Video ansehen1:44:00An ellipse is the locus of all those points in a plane such that the sum of their distances from two fixed points in the plane, is constant. How is it possible to be done? @EDIT To work with horizontal and vertical ellipses in the coordinate plane, we consider two cases: those that are centered at the origin and those that are centered at a point other than the origin. $\endgroup$ – When given the coordinates of the foci and vertices of an ellipse, we can write the equation of the ellipse in standard form. An ellipse (and in fact any conic section) is described by an equation of the form.Thanks for the interesting article. That way it should always be correct (also if you change options in stat_ellipse ). An ellipse has two points which are the focus of the . The way I read it, you need 5 points to determine where the ellipse is, and its a/b parameters.To draw this set of points and to make our ellipse, the following statement must be true: if you take any point on the ellipse, the sum of the distances to those 2 fixed points ( blue tacks ) is constant. The formula for finding the area of the circle is A=πr^2. The parameters a a through f f can be found up to that multiple by knowing 5 5 points on the ellipse: Any multiple of this equation describes the same ellipse. Later in the chapter, we will see ellipses that are rotated in the coordinate plane. geom_point() +.Know about the two foci of the ellipse. For more see Parametric equation of an ellipse Things to try.Ellipse can be defined as a set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.Aufrufe: 1,6Tsd.Foci of Ellipse Formula and Coordinates. Because e = 3 2, e > 1, so we will graph a .Left and Canvas. If it is equal to 1, then the point is on the ellipse.The given ellipse is x2 a2 + y2 b2 = 1 . Right-click the place or area on the map.Finding parameters.Fitting an ellipse to a set of data points in python


Using polar coordinates to find the area of an ellipse
How many points are needed to uniquely define an ellipse?
Foci of an Ellipse (How to Find the Foci)
Ellipse (Definition, Equation, Properties, Eccentricity, Formulas)
Ellipse Calculator
Foci of an ellipse from equation (video)
