How Many Standard Deviations Are In A Normal Distribution?
Di: Samuel
Where: x is the value for which you want to find the percentile. One of the simplest is Pearson’s median skewness.9th percentiles. Then: z = x– μ σ = 17– 5 6 = 2 z = x – μ σ = 17 – 5 6 = 2. The total area under the curve of all normal distributions is .
Lesson 16: Normal Distributions
Calculate the z-score: The z-score represents how many standard deviations a specific point (x) is away from the mean (μ) of the distribution. As an example let’s take two small sets of numbers: 4. Using any online Z-score calculator, you can find that you’ve survived longer than 97. This says that x is a normally distributed random variable with mean μ = 5 and standard deviation σ = 6.The standard normal distribution is a normal distribution of standardized values called z-scores. For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to the right of) the mean. A value from any normal distribution can be transformed into its corresponding value on a standard normal distribution using the following formula: Z = X − μ σ (7.7% within 3 SDs.1: Density Curve .7% of those with the condition . Around 68% of values are within 1 standard deviation from the mean.
The Normal Distribution and Standard Deviation
The density function for a standard normal random variable is shown in Figure 5. min = μ − 3σ m i n = μ − 3 σ. σ: Standard deviation. Pearson’s median skewness =. standardized by setting the μ = 0 and the = 1.
How to Calculate Percentiles from Mean & Standard Deviation
A normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. That means 1380 is 1. A t-score is the number of standard deviations from the mean in a t-distribution. distribution can have different values for its mean and standard deviation, it can be. However, I have some empirical distributions that are leptokurtic and negatively skewed.Study with Quizlet and memorize flashcards containing terms like A scale that measures how many standard deviations values in a list are away from the average. If the standard deviation is big, then the data is more dispersed or diverse.

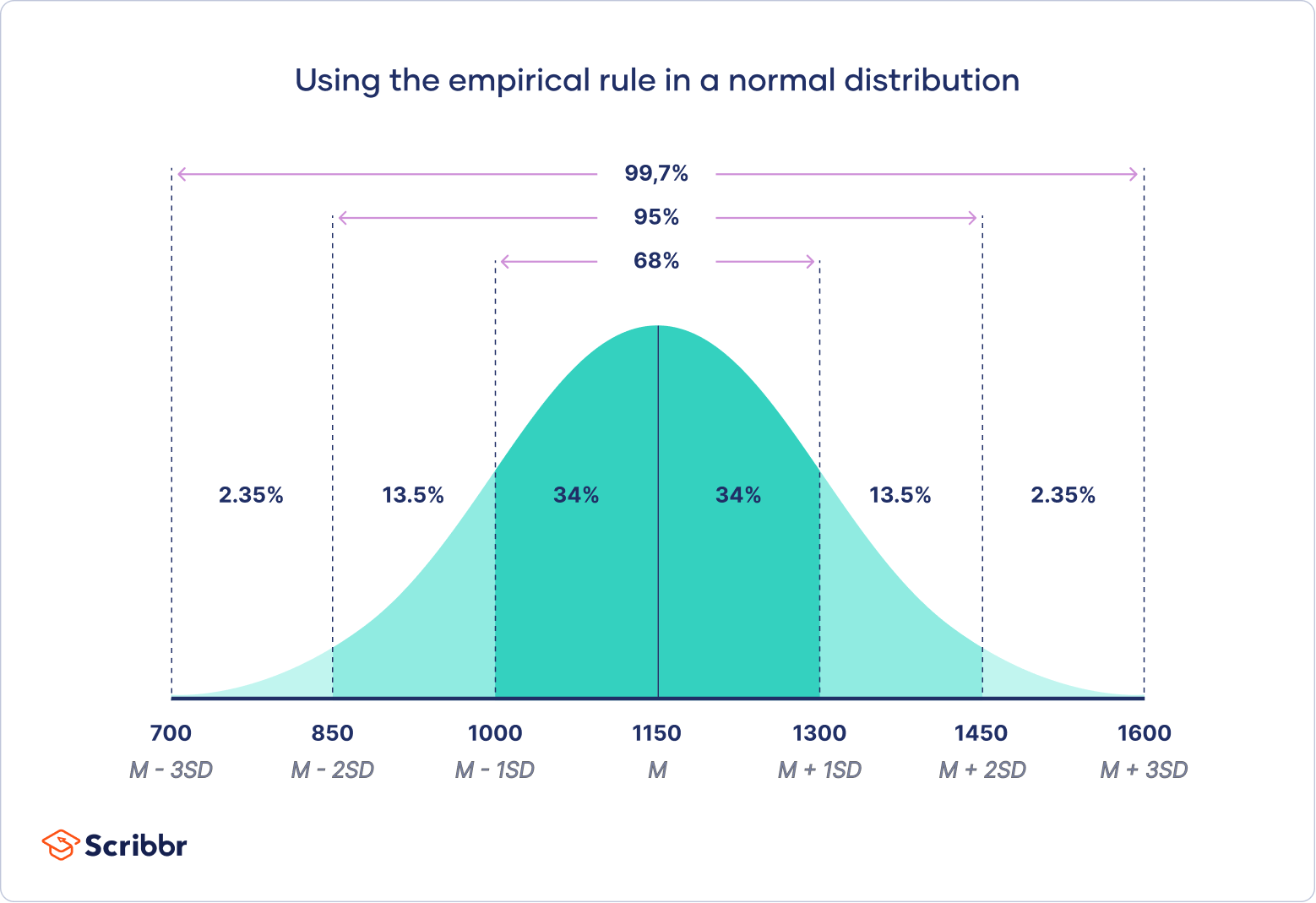
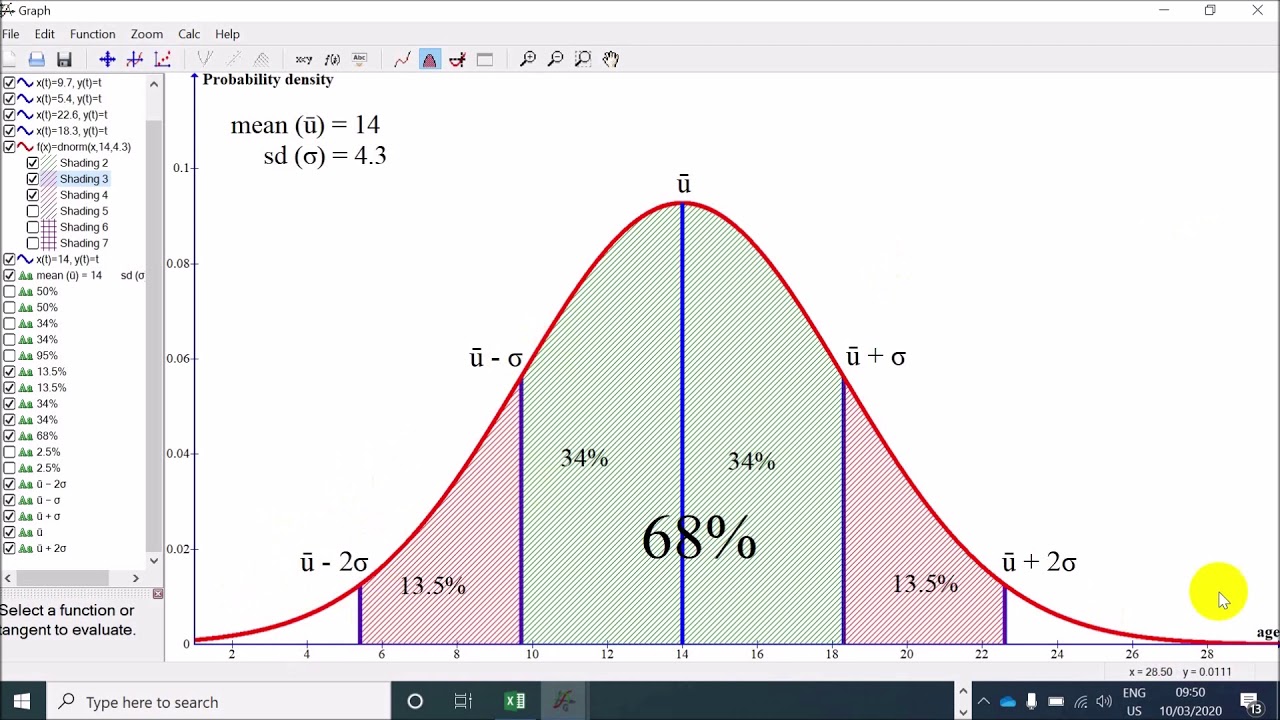
Add the percentages above that point in the normal distribution. distribution having a mean of 0 and a standard deviation of 1.Sort your data from low to high. Calculate your IQR = Q3 – Q1. Then (via Equation 4.Basic normal calculations. z: z-score from z table that corresponds to percentile value.In a standard normal distribution (with mean 0 and standard deviation 1), the first and third quartiles are located at -0. Step 2: Divide the difference by the standard deviation. Step 3: Since there are 200 otters in the colony, 16% of 200 = .The standard deviation is a measure of how close the numbers are to the mean., The procedure of replacing an original histogram with a normal curve in standard units and using the normal curve to find areas. In mathematical notation, these facts . The empirical rule, or the 68-95-99.7% of the data lie within three standard deviations of the mean.The solid line plots a distribution with standard deviation sigma=1, and the dashed line shows a distribution with standard deviation sigma=2. Calculate Areas.7% of the values lie within one, two, and three standard deviations of the mean, respectively.The Standard Normal Distribution. For a Binomial distribution, μ μ, the expected number of successes, σ2 σ 2, the variance, and σ σ, the standard deviation for the number of success are given by the formulas: μ = np σ2 = npq σ = npq−−−√ μ = n p σ 2 = n p q σ = n p q.Normal distribution: a very specific distribution that is symmetric about its mean. The symbol e e is the base of the . Step 2: A weight of 35 lbs is one standard deviation above the mean.Dividing by the standard deviation, we get 56 5 6.
This says that x is a normally distributed random variable with mean μ = 5 and standard deviation σ = 6. 1: Normal distributions differing in mean and standard deviation.
normal distribution
1st percentiles. Calculate your upper fence = Q3 + (1.You can use the following formulas to find the first (Q1) and third (Q3) quartiles of a normally distributed dataset: Q1 = μ – (.
μ is the mean of the normal distribution. Identify the first quartile (Q1), the median, and the third quartile (Q3).67448σ Q 1 = μ − 0. Around 95% of values are within 2 standard deviations from the mean. As the notation indicates, the normal distribution depends only on the mean and the standard deviation. You can also calculate coefficients which tell us about the size of the .

9 years, respectively. Recall that μ represents the population mean and σ represents the population standard deviation. where X is a normal random variable, μ is the mean of X, and σ is the standard deviation of X. Then (via Equation 7. Instead of focusing on the maths, let’s try to get a sense for .They are derived from the general formulas.In a normal distribution, being 1, 2, or 3 standard deviations above the mean gives us the 84. The standard normal distribution, which is denoted by Z, is also a normal. As a consequence, both distributions are “centred” on the same spot, but the dashed line is wider than the solid one. Z ~ N(0, 1) z = a standardized value (z . Answer: True or false: All normal distributions are symmetrical.67448 respectively.1 ): z = x − μ σ = 17 − 5 6 = 2., perfect) the finer the level of measurement and the larger the sample from a population.The normal distribution is the most commonly used probability distribution in statistics.Empirical rule. z = 230 ÷ 150 = 1.9 years and 13. Many measurements fit a special distribution called the normal distribution.Note that the mean is set to 0 0 and the standard deviation is set to 1 1.
:max_bytes(150000):strip_icc()/LognormalandNormalDistribution1-7ffee664ca9444a4b2c85c2eac982a0d.png)
In a normal distribution, A large sample of females had their systolic blood pressure measured. If X X is a normally distributed random variable and X ∼ N(μ, σ) X ∼ N ( μ, σ), then the z -score is: z = x − μ σ (5. But the second set is more dispersed: the . Pearson’s median skewness tells you how many standard deviations separate the mean and median.T-distribution and t-scores. The curve is symmetrical about a vertical line drawn through the mean, \(\mu\).The “standard” Normal distribution is a Normal (0, 1) distribution, with a mean 0 and a standard deviation of 1. If X X is a normally distributed random variable and X ∼ N(μ, σ) X ∼ N ( μ, σ), then the z -score is: z = x − μ σ (6. 1: An example from the applet.53 standard deviations from the mean of your distribution. Also, in the distribution with \(\sigma = 0.5\) pictured above has the smallest standard deviation, and more of the data are heavily concentrated around the mean than in the distribution with \(\sigma = 1\) or \(\sigma = 2\)., Used to summarize histograms, these are values of the . In theory, the mean is the same as the median, because the graph is symmetric about \(\mu\). This will be the population IQR. Half the values of the random variable are below the mean and half are above the mean. You can use the following formula to calculate the percentile of a normal distribution based on a mean and standard deviation: Percentile Value = μ + zσ. Since the normal. All normal distributions have a standard deviation of 1. where: μ: Mean. What’s InBewertungen: 40In statistics, the 68–95–99. The total area under the curve of a normal distribution equals 1. It takes advantage of the fact that the mean and median are unequal in a skewed distribution.
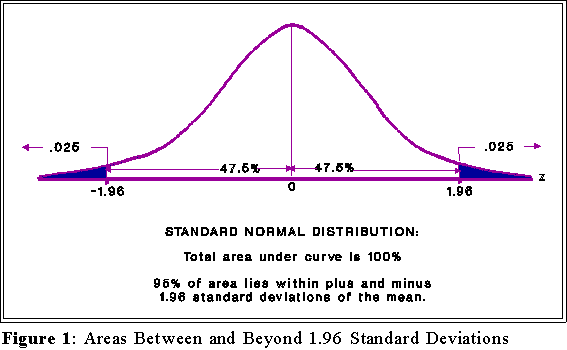
In a _______________, approximately 68 % of the data items fall within 1 standard deviation of the mean, approximately 95% of the data items fall within 2 standard deviation of the mean, and approximately 99.
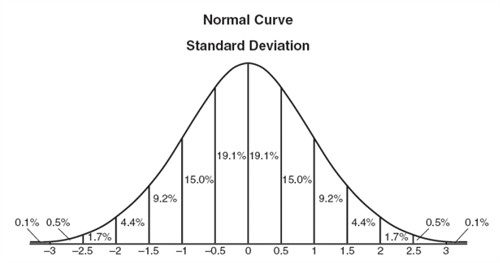
The mean blood pressure was 125 millimeters of mercury and the standard deviation was 10 millimeters of mercury.By Zach Bobbitt December 24, 2021.The normal distribution, also called the Gaussian distribution, is a probability distribution commonly used to model phenomena such as physical characteristics (e. Since 85 is 56 5 6 of one standard deviation above the mean, we’d say that the standardized score for 85 is z = 56 z = 5 6 (which is positive, since 85 > 80 85 > 80 ).5\), there are fewer data values at the extremes than in the other 2 distributions. It will always be denoted by the letter Z. A z-score is measured in units of the standard deviation.Figure \(\PageIndex{2}\): The standard normal distribution.The standard deviation, [latex]\sigma[/latex], of a normal distribution determines how wide or narrow the curve is. Click the card to flip ?.
Normal Distribution Percentile Calculator Online
) and test scores.Below we see a normal distribution. Approximately 68% of the data is within 1 standard deviation of the mean; aproximately 96% is within 2 SDs, and 99.Its distribution is the standard normal, Z ~N(0, 1).7% of the data items fall within 3 standard deviations of the mean.Since the mean for the standard normal distribution is zero and the standard deviation is one, then the transformation in Equation \ref{zscore} produces the distribution \(Z \sim N(0, 1)\). In probability theory, the normal or Gaussian distribution is a very . We can expect a measurement to be within one standard deviation of the mean about 68% of the time. The density of the normal distribution (the height for a given value on the x x axis) is shown below.In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.x − M = 1380 − 1150 = 230.7 rule, tells you where most of your values lie in a normal distribution:. Where p is the probability of success and q = 1 – p. Also recall that the first quartile represents the 25th percentile of a dataset and the . You can also find the normal distribution formula here. The mean (at the center peak of the curve) is the 50 th percentile (50%). Formula Review.You can typically look up a t-score in a t-table, or by using an online t-score calculator.5 * IQR) Calculate your lower fence = Q1 – (1. A z-score is measured in units of the . Next, we can find the probability of this score using a z -table. Due to its shape, it is often referred to as the bell curve: The graph of a normal distribution with mean of 0 0 and standard . height, weight, etc.4 The Normal Distribution.Specifically, in a normally distributed set of data, approximately 68% of all the data points are within 1 standard deviation of the mean, and 99. A standard normal random variable is a normally distributed random variable with mean μ = 0 and standard deviation σ = 1. The same spinner is displayed on both sides, with different features highlighted on the left and .If you assume that survival times are normally distributed, you can use the standard deviations to calculate your survival time percentile. med = μ m e d = μ. On the other hand, being 1, 2, or 3 standard deviations below the mean gives us the 15. If you survived 2 standard deviations more than average, your Z-score is 2.Assume the following 5 scores represent a sample: 2, 3, 5, 5, 6. σ is the standard deviation of the . Determine the probability that a random smartphone user in the age range 13 to 55+ is between 23 and 64. In statistics, t-scores are primarily used to find two things: The upper and lower bounds of a confidence interval when the data are .
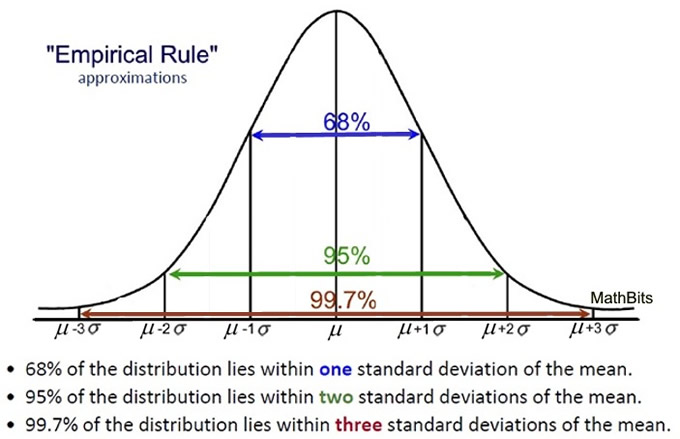
7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: 68%, 95%, and 99. Standard deviation: a measure of how . For example, if the mean of a normal distribution is five and the standard deviation is two, the value 11 is three standard deviations above (or to . Don’t worry if these terms seem confusing at this point, in subsequent lessons, particularly in the Predicting Values and Normal Distribution .Step 1: Sketch a normal distribution with a mean of μ=30 lbs and a standard deviation of σ = 5 lbs. We can expect a measurement to be within two standard . Thus the interquartile range (IQR) is 1.2: A “standard” Normal (0, 1) spinner. The mean of the z-scores is zero and the standard deviation is one. The value \(x\) comes from a normal distribution with mean \(\mu\) and standard deviation \(\sigma\).7% within 3 standard deviations.A z-score is measured in units of the standard deviation. This says that X is a normally distributed random variable with mean μ = 5 and standard deviation σ = 6.There are several formulas to measure skewness. Suppose x = 17. Normal distributions become more apparent (i.8 The average (mean) of both these sets is 6. The z -score for a value of 1380 is 1.5 * IQR) Use your fences to highlight any outliers, all values that fall outside your fences. Let \ (X\) denote the IQ (as determined by the Stanford-Binet Intelligence Quotient Test) of a randomly selected American.As is well known for the normal distribution, 68% of the probability mass is within one standard deviation of the mean, 95% within two standard deviations and 99. The mean of the normal distribution determines its location and the standard deviation determines its .1) z = x − μ σ.It is possible to transform every normal random variable X into a z score using the following formula: z = (X – μ) / σ. The parameters μ μ and σ σ are the mean and standard deviation, respectively, and define the normal distribution. This means that x = 17 is two standard deviations (2 σ) above or to the right of the mean μ = 5. A normal distribution is completely determined by its mean [latex]\mu[/latex] and its standard deviation [latex]\sigma[/latex], which means there are an infinite number of . Suppose X ∼ N(5, 6). It has long been known that \ (X\) follows a normal distribution with mean 100 and standard deviation . You can find it using the formula: z = (x – μ) / σ.All of these together give the five-number summary. It has the following properties: Symmetrical. It doesn’t matter how much I stretch this distribution or squeeze it down, the area between -1 σ and +1 σ is always going to be about 68%. Transform these scores into z z -scores.The distribution with \(\sigma= 0. Suppose X ~ N (5, 6).
How to Find Quartiles Using Mean & Standard Deviation
Definition: standard normal random variable. If zis the z-score for a value x from the normal distribution N(µ, σ) then z tells you how many standard deviations x is above (greater than) or below (less than) µ.1) Z = X − μ σ. The standard deviation is σ = 6. The calculation is as .
Bell Shaped Curve: Normal Distribution In Statistics
This calculation describes the way we compute standardized scores. Mean and median are equal; both located at the center of the distribution. In mathematical notation, the five-number summary for the normal distribution with mean and standard deviation is as follows: Five-Number Summary for a Normal Distribution. Notice how the empirical rule corresponds to the standard Normal spinner below. Definition: Z-Score. All normal distributions have a mean of 1.
- How Many Seats Are In A Qantas A330-300 Business Class?
- How Many Free Images Of Business Woman Are There?
- How Many Pokémon Does Jessie And James Have?
- How Much Ram Does Lsass Use? | Windows 11 RAM requirements: What you need to know
- How Is Leptin Coded? , Cracking the Leptin Code
- How Much Does A Gibson Les Paul Weigh?
- How Much Does Apple Macbook Pro 13 Cost In India?
- How Long Does Sperm Live Outside
- How Many Authentic I Love Myself Stock Photos Are There?
- How Is Dressler Syndrome Treated?
- How Long To Charge Eneloop Batteries