BAHTMZ

General

Gradient Of Tangent _ Gradients and Graphs

Di: Samuel

The function’s first derivative = f‘ (x) = (2) (0. Once we’ve got the slope, we can . In the first cell of your worksheet, change x1 to 0. Slope of Tangent Line to the Circle: 7. The gradient between the centre and the point given is -2.STEP 2: Find the gradient of the tangent; STEP 3: The equation of the tangent is the equation of the line with that gradient that goes through point P (see Equation of a Straight Line) Exam Tip. So basically, the Gradient vector is applicable only in a scalar field and the Tangent vector belongs to the vector. dy/dx = 2x + 3.Video ansehen11:58More resources available at www.

How to Find the Equation of a Tangent Line

Find the equation of the line tangent to the graph of f(x) = 1 / x at x = 2. Finding the tangent line to a point on a curved graph is challenging and requires the use of calculus; specifically, we will use the derivative to find the slope of the curve.Find the Gradient of the Tangent Line with a Given Point.

Tangent Line -- from Wolfram MathWorld

So for f (x,y), which is 3D (or in R3) the gradient will be 2D, so it is standard to say that the vectors are on the xy plane, which is what we graph in in R2.Drawing a tangent to a curve using a ruler. This follows easily from the definition of a tangent line, but is also easy to see with the “slope = derivative” idea: a straight line’s slope (i. For any point on the curve we are . I can draw these asymptotes. The methods developed in this section so far give a straightforward method of finding equations of normal lines and tangent planes for surfaces with explicit equations of .Substitute the gradient of the tangent and the coordinates of the given point into an appropriate form of the straight line equation. y = -\dfrac{12}{5}x + c,

How to Find the Equation of a Tangent Line: 8 Steps

This allows us to calculate rates of reaction at specific times along the x-axis.The tangent point is at (0, 5). Plug any value a for x into this equation, and the result will be the slope of the line tangent to f (x) at the point were x = a. 5-a-day GCSE 9-1; 5-a-day Primary; 5-a-day Further Maths; More. Further Maths; GCSE Revision; Revision Cards; Books; Equation of a Tangent to a Curve Video . \[m_{\text{tangent}} \times m_{\text{normal}} = -1\] Worked example 13: Finding the . The notion of gradient is the derivative of a scalar function of many variables. Solution: For the function f(x, y) = x2 + y2 , we have: fx(x, y) = 2x. Given a function f(x), described by a curve y = f(x), we find the equation of the tangent to the curve at a point P(a, b) along its length, in two steps : Step 1: find the gradient of the curve at point P(a, b) P ( a, b) , this equals to the gradient of the tangent.Now, by observing that this line is a radius, and that tangents are perpendicular to the radius, we can find the gradient of the tangent by taking the negative reciprocal of the answer we got above.In the third mini-lecture, we use our work from the previous mini-lecture to define the derivative at a point on a curve as the equation for the gradient of the tangent at that point on the curve.Finding the derivative (gradient) of the curve at point. Use implicit differentiation to find an equation of the tangent line to the curve at the given point. Find the arc length of the teardrop. x-axis to the Point of Tangency: 3. remember, perpendicular gradients multiply to -1 (they are negative reciprocals) A Level AQA Edexcel OCR. This may be referred to as the change in \ (y\) divided by . EXTRA STEP: Find the negative reciprocal of the gradient.The gradient is always one dimension smaller than the original function.The tangent line to a curve at a given point is the line which intersects the curve at the point and has the same instantaneous slope as the curve at the point.The gradient of a line is calculated by dividing the difference in the \ (y\)-coordinates by the difference in the \ (x\)-coordinates. On a diagram, draw the circle and the tangent at the point P (3, -4) and draw the radius from the centre (0, 0) to the point P. To calculate the rate of a reaction from a rate graph, a tangent must first be drawn to the curve.comAutor: Eddie Woo

D2 : Gradients, Tangents and Derivatives

To attain a better approximation of the slope at that point, let’s try decreasing the distance between the two points at either side of it. Multiply this by -1 (change the sign) to get the gradient of the tangent, gradient =-3.

How to calculate a gradient using a tangent

First, find \(m\), the gradient of the tangent. You then find the gradient of this tangent. Calculate the negative reciprocal of this gradient to find ‘m’ The gradient of the tangent to a circle is perpendicular to the gradient from the centre to the .The graph of the parametric equations x = t(t2 − 1), y = t2 − 1 crosses itself as shown in Figure 9. And so the graph of tangent, the graph of tangent of theta is going to look, is going to look something like this. Curve being tangent to a surface. Use this information to find areas, accelerations and velocities. Let me draw that and that.Recall the power rule when taking derivatives: . Let’s denote the gradient of the tangent m_T and gradient of the normal m_N.Click here for Answers. Enter the x value of the point you’re investigating. The gradient at a point on a curve is defined as the gradient of the tangent to the curve at that point.Calculating the gradient of a tangent of a radial function.Aufrufe: 1,3Mio. Theta θ in Radians: 5. So, if we want strong gradients and big learning steps, we should use the tanh . This means we’ll integrate from t = − 1 to t = 1. Next: Algebraic Proof Practice Questions.2 Find the gradient of the tangent at that point.The tangent line to a straight line is the straight line itself.To find the gradient of a curve, you must draw an accurate sketch of the curve. If we draw in the tangents to the curve, you will notice that if the gradient of the tangent is .Learn how to construct and use tangents to find gradients of curves.5 and evaluate.In this lesson we discuss what a tangent is and how to calculate the gradient using a tangent. I was under the impression we can apply Tangent vectors to scalar field. \text{Gradient of tangent } = -\dfrac{12}{5} So, we know the straight-line equation for our tangent must be of the form . We now have the gradient of the tangent line, -3, so we . 3 Find the \textbf{y} -intercept and hence the equation of the tangent.What we want is a line tangent to the function at (1, 1/2) — one that has a slope equal to that of the function at (1, 1/2). The gradient at that point is.

Prologue to Calculus (5 of 5: Gradient of the tangent)

So if we increase the value of the argument of a function by an infinitesimal amount, then the resulting change in the value of the function, divided by the infinitesimal will give the slope (modulo taking the standard part by discarding any remaining infinitesimals). Use the tangent to calculate the rate of reaction as shown below: Obtaining a tangent on a curve.

Differentiation Increasing and decreasing functions

The normal to a curve is the line perpendicular to the tangent to the curve at a given point.This short Tassomai tutorial video explains how to find the gradient at a particular point of a curveIt will help you learn and revise content required for t. This will be the gradient of the normal. So the tangent plane is. and the normal line is.

Differentiation I: Straight Lines and Gradients

Equation of a tangent that passes through a point not on the curve .

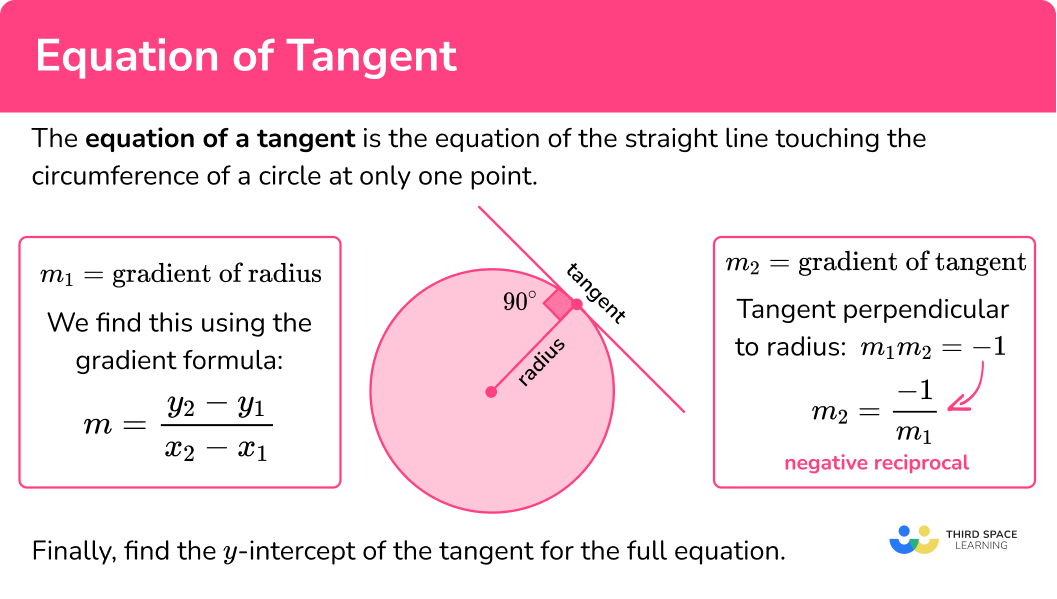
Equation Of Tangent - GCSE Maths - Steps, Examples, Worksheet

The gradient of the curve at P(a, b) A normal is a straight line perpendicular (at right angle 90°) to a curve.3 Equation of a tangent to a circle Practice Questions. We can see by the parametrizations of x and y that when t = ± 1, x = 0 and y = 0. The Corbettmaths Practice Questions on the Equation of a Tangent to a Circle.Tangent Line of a Circle. The gradient of a tangent = Gradient of a curve at that point. Example-1: Find the equation of the tangent plane to the surface z = x2 + y2 at the point (1, 2, 5).

Find the Gradient of the Tangent Line with a Given Point

In the fifth mini-lecture, we introduce the derivatives of common . Previous: Multiplying Matrices – 2×2 . derivative) never changes, so its tangent line—having the same slope—will be parallel and hence must coincide with the straight . These vectors have no z coordinate to them, just x and y. At the point where you need to know the gradient, draw a tangent to the curve.1 Gradients, Tangents & Normals for the Edexcel A Level Maths: Pure syllabus, written by the Maths experts at Save My Exams. f‘ (x) = x + 3.Revision notes on 7. A tangent is a line that just touches the curve but doesn’t go through it. As a warm-up example, we’ll find the tangent plane and normal line to the surface at the point To do so, we just apply Theorem 2. Your graph should now look .The gradient when y=x^2-9x is -7 The gradient when y=x^2-9 is 2 Finding the point of intersection of two parabolas means that your two equations are equal at a point x^2-9=x^2-9x -9=-9x x=1 When x=1, y=-8 –> (1,-8) To find the gradient of the lines at (1,-8), we need to find the first derivative y=x^2-9 (dy)/(dx)=2x Therefore, when we sub x=1 . This vector is useful for example to compute tangent lines or tangent planes.How to Compare the Tangent and Normal. mtan = limx → 2f ( x) − f ( 2) x − 2 Apply the definition. GRADIENT = ∆ (PRODUCT) ÷ ∆ (TIME) You can use this formula to calculate the gradient at any particular point in the curve. These derivatives correspond to each of the independent variables and can be interpreted as instantaneous rates of change (that .

Gradients and Graphs

Theta θ is the Angle (in Degrees) from the Pos. De nition: The gradient of a function f(x;y) is de ned as rf(x;y) = [f x(x;y);f y(x;y)] : For functions of three variables, de ne

The equation of the tangent to a circle

The reciprocal of =\cfrac{1}{3} is 3. We also use an exam example to show you how to complete the ta.34, forming a teardrop. The formula m = y2−y1 x2−x1

How do you find the gradient of a tangent? (full question below)

Find the gradient of the curve y = x² at the point (3, 9). This means that using the tanh activation function results in higher gradient values during training and higher updates in the weights of the network.Unit 12: Tangent spaces Lecture 12.

Circle Graphs and Tangents Worksheets, Questions and Revision

Evaluating this for the two points, which equals -2.Our tangent plane calculator also follows the same procedure as used in these examples and you can get exactly same result in seconds.

Tangent | Definition | Equation and Calculator - Cuemath

Use the gradient to find the tangent to a level curve of a given function.Differentiate algebraic and trigonometric equations, rate of change, stationary points, nature, curve sketching, and equation of tangent in Higher Maths. Calculate directional derivatives and gradients in three dimensions. FIND THE GRADIENT OF THE TANGENT LINE WITH A GIVEN POINT.Below is the graph of a quadratic function, showing where the function is increasing and decreasing. The gradient is found using .

Gradients, Tangents and Normals

Additionally, we observe that the gradient of tanh is four times greater than the gradient of the sigmoid function. You can find this by differentiating the equation of the curve, and substituting in. = limx → 21 x . Log InorSign Up.Siyavula’s open Mathematics Grade 12 textbook, chapter 7 on Analytical geometry covering 7. A function \(z=f(x,y)\) has two partial derivatives: \(∂z/∂x\) and \(∂z/∂y\). Can someone provide the formal definition of the tangent line to a curve? 1. R is the Radius of the Circle: 1.

Gradient of the tangent to the curve

Worked example. A tangent is a straight line which touches the curve at one point only.Free tangent line calculator – find the equation of the tangent line given a point or the intercept step-by-step In the fourth mini-lecture, we calculate the derivative of various basic functions from first principles.Method: Equation of the Tangent to a Curve. This is also the gradient of the tangent line. Welcome; Videos and Worksheets; Primary; 5-a-day. The negative reciprocal of is. It was quite foolish of me to mesh the 2 concepts together.

Gradients of tangents to curves | Teaching Resources

This means that we must have.Gradients calculated using a tangent represent the gradient of the curve at the point where the two lines meet.

Tangents to a Curve - WORKED EXAMPLE - GCSE Physics - YouTube

Previous: Frequency Trees Practice Questions. We can use Equation, but as we have seen, the results are the same if we use Equation. Calculating Rates of Reaction using Tangents. Intellectual Math. The gradient of the radius =\cfrac{1}{3}.

Activation Functions: Sigmoid vs Tanh

This video explains how to find the Equation of a Tangent to a Curve. Learn Math step-by-step. Make \(y\) the subject of the formula. m_T\cdot m_N = -1. If you understand the formula in Step 2 above, you can find the gradient of the tangent without having to find the gradient of the radius first.

Calculating Gradients From Tangents

The Gradient and Normal Lines, Tangent Planes. A TANGENT just touches a circle (but does not cross it) The gradient of the tangent at point P is PERPENDICULAR to the gradient of the radius OP. These derivatives correspond to each of the independent variables and can be interpreted as instantaneous rates of change (that is, . Put x = 2, dy/dx = 2(2) + 3 = 4 + 3 . For a pair of tangent and normal lines at one point, we have one rule: The two must be perpendicular.D2 : Gradients, Tangents and Derivatives Gradient of a Curve In this module we are concerned with finding a formula for the slope or gradient of the tangent at any point on a given curve y=f(x).The slope of the tangent line is the instantaneous slope of the curve.First, make sure you are familiar with Equations of Straight Lines and Perpendicular Gradients. Find the gradient of the tangent to the curve at the point indicated : Problem 1 : y = x² + 3x (2, 10) Solution : y = x² + 3x.This structured practice takes you through three examples of finding the equation of the line tangent to a curve at a specific point. And we could obviously, it’s periodic, we could just keep doing it on and on and on in both directions. We can calculate the slope of a tangent line using the definition of the derivative of a function f at x = c (provided that limit exists): lim h → 0 f ( c + h) − f ( c) h.Let me go back, pi, and I can draw these asymptotes. It produces a vector. We know that differentiation is the process that we use to find the gradient of a point on the curve. For example, suppose we want . That was pretty simple — find the partial derivatives and substitute in the coordinates.