Gezinkter Würfel Wahrscheinlichkeit
Di: Samuel
Gefragt 15 Jan 2018 von -sa. Die eingeführten Begriffe sollen beispielhaft anhand des Werfens eines herkömmlichen Spielwürfels veranschaulicht werden: Diese Festlegung der Ergebnisse und des Ergebnisraumes ist bereits Teil der mathematischen Modellierung, die dem jeweiligen Kontext angemessen erfolgen sollte.4-seitiger gezinkter Würfel. Bei diesem Zufallsexperiment ist egal, ob du erst das Glücksrad drehst oder erst würfelst.
Wahrscheinlichkeit
gezinkt; wahrscheinlichkeit; würfel; augensumme; wahrscheinlichkeitsrechnung + 0 Daumen.1 Geldfälscher 14 25 VI.
Mit dem Würfel wird 100-mal nacheinander gewürfelt. meine Aufgabe ist es einen gezinkten Würfel zu programmieren, der mit 95% Wahrscheinlichkeit eine 6 ausgibt und mit jeweils 1% Wahrscheinlichkeit eine 1,2,3,4 oder 5 ausgibt. Ich denke, du verstehst, was ich meine. Problem/Ansatz: Mit welcher Wahrscheinlichkeit gewinnt A, wenn beide Würfel einmal geworfen werden und die höhere Augenzahl gewinnt? (Geben Sie das Ergebnis in . Beide haben die Ziffern 1,2,3,4 aufgedruckt. zwei 4seitige gezinkte Würfel, beide haben die Ziffern 1,2,3,4 aufgedruckt.1 Würfeln mit einem gezinkten Würfel 11 25 V. Wenn jede Augenzahl Wahrscheinlichkeit 1/6 hat, ist das schon einmal ein Indiz für Zufälligkeit, aber der Würfel kann trotzdem gezinkt sein.Bei einem „gezinkten Würfel“ beträgt die Wahrscheinlichkeit, eine „6“ zu würfeln, nur 10 %. folgende Wahrscheinlichkeiten gegeben:
Entropie: Wahrscheinlichkeit
würfel; wahrscheinlichkeit; augensumme + 0 Daumen. die 6 wird wirklich mit einer deutlich höheren Wahrscheinlichkeit .; Peter ist sich fast sicher, dass der rote Würfel, den er gerade in der Hand hat, der faire Würfel ist.Alle anderen Zahlen mit einer Wahrscheinlichkeit von . Nach 12 Würfen müsste sich demnach die Wahrscheinlichkeit ergeben, dass jeweils nach 4 .Zum Seitenanfang : Bevor wir zur Berechnung von Wahrscheinlichkeiten kommen, müssen wir wissen, was sie bedeuten.
ein 6-seitiger gezinkter Würfel
Ein sechsseitiger Würfel wird manipuliert.Peter besitzt zwei Würfel: [:] Fairer Würfel: Jede Zahl wird mit einer Wahrscheinlichkeit von geworfen. Berechnen Sie die Wahrscheinlichkeit für ein Durchkommen bei einem . Wenn wir unseren Würfel aus einer Kiste mit 9 999 intakten und einem gezinkten Würfel herausgreifen, dann ist die Wahrscheinlichkeit dafür, dass unser Würfel der gezinkte ist, sehr klein, auchWenn es sich um einen fairen Würfel handelt (alle Seiten haben die gleiche Gewichtung), ist die Wahrscheinlichkeit für jedes dieser Ergebnisse gleich 1 zu 6 oder 1/6. Gefragt 16 Feb 2016 von Gast. In der Mathematik stellen wir dies meistens in einem Baumdiagramm dar. Zu jedem Ergebnis gibt es einen Pfad. ein 6-seitiger .Die erste Möglichkeit ist erstmal zu gucken, ob der Würfel wirklich gleichverteilt ist.
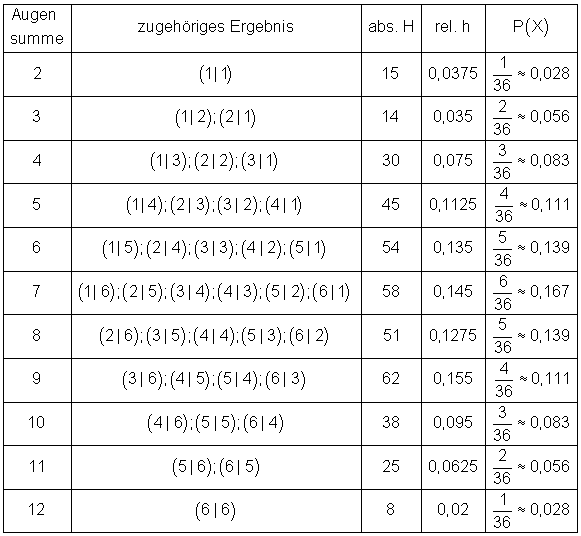
Wie groß ist die Wahrscheinlichkeit, dass die Augensumme
Aufgabe 2: Mit welcher Wahrscheinlichkeit würfle ich mit 2 Würfeln zwei 6-er? Möglich sind die folgenden Würfelkombinationen: 1 1 2 1 3 1 . ? Siehe Wahrscheinlichkeit im Wiki. Die Wahrscheinlichkeiten der Augenzahlen sind der folgenden Tabelle zu entnehmen: \end {tabular} Wie groß ist die Wahrscheinlichkeit einer Augensumme von 10 ? 10? (Geben Sie das Ergebnis in Prozent an. Die könntest du aufzählen und ihre Wahrscheinlichkeiten bestimmen. P3 = 0,3256 für 20-seitige Würfel.1: Berechne die Wahrscheinlichkeit, dass genau 10 Sechsen auftreten. Um die Mathematik hinter dem Zufall zu verstehen, beschäftigen wir uns mit zwei Beispielen: zum einen mit dem einmaligen Werfen einer Münze, zum anderen mit dem einmaligen Werfen eines Würfels. Berechne die Wahrscheinlichkeit, dass mindestens .random erstellt.
Wahrscheinlichkeitslehre mit Würfeln
Gezinkter Würfel Erwartungswert
6 seitiger-gezinkter Würfel. drei Sechsen oder drei Vieren? Das können wir leicht ausrechnen: Die Wahrscheinlichkeit, mit einem Würfel eine Sechs zu werfen, ist genau 1/6. Mit welcher Wahrscheinlichkeit würfelt man eine gerade Zahl Meine Ideen: Mein Problem . Und wenn dies nicht der Fall ist, gehen wir davon aus, dass der Würfel gezinkt ist.[:] Gezinkter Würfel: Die Zahl 6 wird mit einer Wahrscheinlichkeit von geworfen. An Hand einer Münze oder eines Würfels hat jeder eine ganz gute Vorstellung von der Wahrscheinlichkeit.3 Der Schein kann trügen 14 26 VII. Gefragt 13 Jun 2018 von Gast.Würfeln Würfel mit dem abgebildeten Netz trägt die Nummern 1, 2 und 3.
Münzwurf Wahrscheinlichkeit Rechner
Die Wahrscheinlichkeiten der Augenzahlen sind den folgenden Tabellen zu entnehmen:
Würfeln mit einem gezinkten Würfel
Ein 6-seitiger, gezinkter Würfel mit den Augenzahlen 1, 2, 3, 4, 5, 6 wird zweimal geworfen. Die Zufallsvariable X zählt die Anzahl der Sechsen.Aufgabe: Man betrachte zwei 4 -seitige, gezinkte wurfel. Die Wahrscheinlichkeit der Augenzahlen sind der folgenden Tabelle entnehmen: Die Wahrscheinlichkeit der Augenzahlen sind der . Der gezinkte Würfel ist sofort durch das Gewicht zu erkennen. Dazu müssen wir doch wis-sen, wie viele gezinkte und nicht-gezinkte Würfel es überhaupt gibt. Das funktioniert aber sehr gut, d. Wahrscheinlichkeit Würfeln 1. Einfache Beispiele:
Zufallsexperimente: Münz- und Würfelwurf
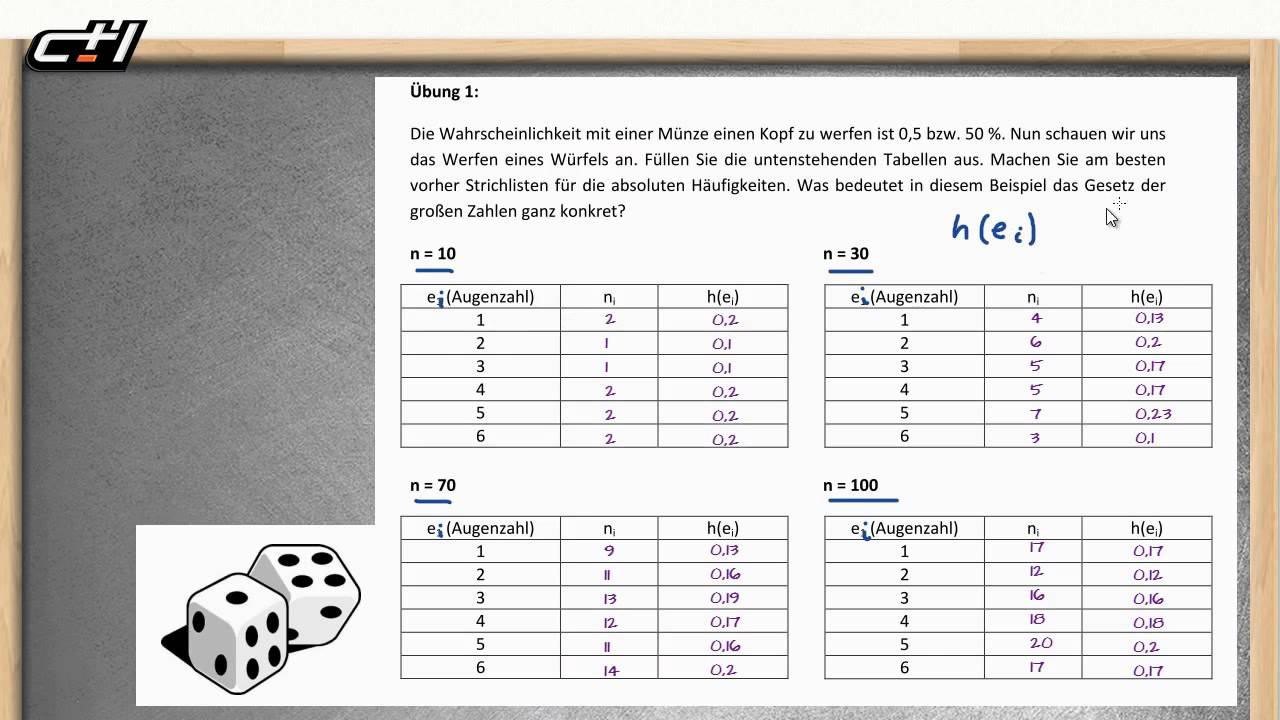
1 Mittelwert der Körpergröße 15 VII. Mit einem Tabellenkalkulationsprogramm können Zufallsexperimente, wie das Werfen einer Münze oder das Würfeln simuliert werden. Jeder Aufruf entspricht einem Wurf des gezinkten Würfels.Wenn wir ihn werfen, muss er auf eine der 6 Flächen fallen, jede Fläche kommt mit der Wahrscheinlichkeit von 1/6 nach oben. Die Wahrscheinlichkeit, mit drei Würfeln drei Sechsen zu werfen, ist dann 1/6 * .) Problem/Ansatz: Hallo, laut mir .Das Maß für die Sicherheit, die höchste Augenzahl 6 zu würfeln, könnte vielleicht so formuliert werden: Ungefähr bei . Die Wahrscheinlichkeiten der Augenzahlen sind der folgenden Tabelle zu .Aufgabe: Ein 6-seitiger, gezinkter Würfel mit den Augenzahlen 1, 2, 3, 4, 5, 6 wird zweimal geworfen. Du siehst im zweistufigen Baumdiagramm die Ergebnismenge. Die Baumdiagramme zeigen dir die möglichen Ergebnisse.Wie können wir diesen Würfel mit unserer weighted_choice-Funktion simulieren? Wir rufen weighted_choice mit den Augenzahlen des Würfels und der Liste der korrespondierenden Gewichte auf.Ich erzeuge einen Würfel, indem ich ein neues Objekt der Klasse erzeuge. eine 6 zu erhalten, ist also 1/6. Wie man aus der Formel von Shannon erkennen kann, sind die beiden Begriffe eng verwandt. Computergestützte Stochastik VII. Mit welcher Wahrscheinlichkeit gewinnt A? Gefragt 16 Jan 2019 von nik. Das ruft nun den Konstruktor auf.

Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als 11 ist? (Geben Sie das Ergebnis in Prozent an. Die Umrechnung in Prozent nicht vergessen. Wie ändere ich nun in Java die Wahrscheinlichkeiten für das Eintreten eines Falles?Wie groß wird die Wahrscheinlichkeit sein, beim Würfeln mit drei Würfeln spontan einen geordneten Zustand herzustellen, z. Die Wahrscheinlichkeit, bei einem Würfelwurf z. Etwas Arbeit könnte man sparen, wenn man die Symmetrie ausnutzt.Anders ist dies bei einem gezinkten Würfel, denn hier wird nichts dem Zufall überlassen: Die Wahrscheinlichkeit, dass beim gezinkten Würfel die Sechs fällt, liegt bei (fast genau) 100 Prozent. Gefragt 16 Jan 2019 von Samuel123. Bei einem sechsseitigen Würfel ist die Wahrscheinlichkeit für alle Ziffern genau gleich. Gehen wir von einem der einfachsten Zufallsexperimente aus: dem Würfel (Beispiel 1 oben).3 Wahrscheinlichkeiten beim Reißnagelwurf 13 VI. Werfen eines unfairen (= gezinkten) Würfels. Zusammengenommen ist es 1/4 + 1/6 = 3/12 + 6/12= 9/12=3/4. Somit beträgt die Chance eine bestimmte Zahl zu würfeln, bei allen Zahlen 1/6. Die Aufgabe lautet: Die 6 ist doppelt so wahrscheinlich und die 1 halb so wahrscheinlich, wie die übrigen 4 Augenzahlen. Wir sehen, dass nach 10.Wahrscheinlichkeit am Beispiel Würfel – Mathe. jede Seite ist gleich wahrscheinlich – oder ich gebe explizit die Wahrscheinlichkeiten der einzelnen Seiten an.Man betrachte zwei vierseitige Würfel.2 „Montagsfahrräder“ 14 26 VI.Schließe mich den anderen Rezensionen an. Unfairer Würfel, Stochastik . Wie groß ist die Wahrscheinlichkeit für eine Augenzahl größer als 5? Die Wahrscheinlichkeiten für die Ergebnisse bleiben .der Würfel gezinkt ist. Wahrscheinlichkeit für Wappen: p (W) = 0,6.Ein 6-seitiger, gezinkter Würfel mit den Zahlen 1,2,3,4,5,6 wird zweimal geworfen. Leider ist auch das Würfelverhalten nicht normal, d. Im Folgenden finden Sie eine Anleitung im PDF-Format, wie man . Rückschlüsse aus Baumdiagrammen VI. weiß ich nicht wie ich weiter vorgehen muss: Beim Würfeln mit einem gezinkten Würfel sind für die Ereignisse. wahrscheinlichkeit; gezinkt; würfel; unfair + 0 Daumen. Wahrscheinlichkeit für Zahl: p (Z) = 0,4. Der erste Würfel A hat die Ziffern 1,3,7,7 aufgedruckt, der zweite Würfel B hat die Ziffern 3,3,6,7 aufgedruckt., A 6 A_1, A_2,\dots, A_6 A 1 , A 2 , .2 Würfeln mit einem Stein 12 V.) Da kommt nur (6 und 6) in Frage und P ( (6 und 6) ) = 0. Es befindet sich unter der Augenzahl Eins, so dass der gezinkte Würfel in der Regel mit der schweren Seite . Beantwortet 14 Jan 2018 von Lu 162 k ?.Intuitiv ist es schwierig, den wahrscheinlichsten Erfolg abzuschätzen, aber mit unserem Rechner hast du alle Wahrscheinlichkeiten in einem Wimpernschlag überblickt.
4 seitiger Würfel Wahrscheinlichkeit A gewinnt
Folgt der Würfel der Zahlenfolge 1-2-3-4-5-6-1-2-.
Bestimmen Sie die Varianz und Standardabweichung. w = Anzahl günstige Fälle / Anzahl mögliche Fälle = 1/6 = 0.Ein 6 -seitiger, gezinkter Wurfel mit den Augenzahlen 1,2,3,4,5,6 wird zweimal geworfen. A= Es wird eine gerade Zahl geworfen, B= Es wird eine Augenzahl kleiner oder gleich 3 geworfen, C= Es wird eine 1 oder eine 4 geworfen. Beim 4seitigen Würfel 1/4.Hallo 🙂 Ich hab ein Problem beim bestimmen einer Wahrscheinlichkeit: Und zwar wird mit einem gezinkten Würfel, bei dem die 6 dreimal häufiger auftritt als andere Zahlen (die Zahlen von 1-5 jedoch gleichhäufig auftreten) zunächst nur einmal gewürfelt und man soll die Wahrscheinlichkeit berechnen, mit der eine gerade Zahl ., A 6 nicht alle .Eine 6-seitiger, gezinkter Würfel mit den Augenzahlen 1,2,3,4,5,6 wird zweimal geworfen. Ω = { Ω = { WW, WZ, ZW, ZZ } }. Die Wahrscheinlichkeiten der Augenzahlen sind der folgenden Tabelle zu entnehmen: Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als 10 ist? Zunächst lernst du, dass es sich beim Würfelwurf um einen Zufallsversuch, genauer gesagt um ein Laplace-Experiment, handelt, und anschließend siehst du einige Beispiele zur Berechnung von .Mit welcher Wahrscheinlichkeit gewinnt Würfel A, .Für einen gezinkten Würfel sei P(X=k) = 1/21 k mit k=1,2,.Bei folgender Aufgabe fehlt mir ein Ansatz bzw. Wenn man weiß, dass der Würfel immer auf eine bestimmte Seite fallen wird, zum Beispiel auf die 5, können die Ereignisse A 1, A 2, .Am Anfang wenden wir uns der Berechnung der Wahrscheinlichkeiten eines völlig normalen Würfels zu.000 Würfen die geschätzte Wahrscheinlichkeit der Gewichtung entspricht der Würfel wackelt manchmal ungewöhnlich, bevor er auf der 6 liegen bleibt. Beste Mathematiker Community-Chat. Im folgenden Text wird die Wahrscheinlichkeit am Beispiel eines Würfels einfach erklärt. gezinkt; wahrscheinlichkeit; würfel; stochastik; Liveticker Loungeticker.Beim 6seitigen Würfel ist die Wahrscheinlichkeit, dass eine 7 kommt, 1/6. 6-seitiger gezinkter Würfel.Viele übersetzte Beispielsätze mit gezinkte Würfel – Englisch-Deutsch Wörterbuch und Suchmaschine für Millionen von Englisch-Übersetzungen. Dabei gebe ich entweder nur die Anzahl Seiten an – die Wahrscheinlichkeit ist dann eine Gleichverteilung, d. Die Augenzahlen bei einmaligem Würfeln weisen die unten angegebene Wahrscheinlichkeitsfunktion auf: 1/9 für x=4,5,6. Für Nachhilfe buchen.
Zufall und Wahrscheinlichkeit
Beispiel: Eine gezinkte Münze wird zweimal geworfen.Gezinkter Würfel. Wahrscheinlichkeit Augensumme grösser als 11 .
Person A hat einen 20-seitigen .Der Begriff Wahrscheinlichkeit wird von den meisten Menschen viel eher verstanden, als der Begriff der Entropie., dann ist der Würfel gleichverteilt, aber nicht zufällig .Eine intuitive Interpretation von Wahrscheinlichkeit ist allerdings bekannt: Die Bedeutung von P ({ 6 }) = 1/6 beim Würfeln ist, dass jeder sechste Wurf eine 6 ergibt — was genau mit gemeint ist, muss aber noch erklärt werden. Gefragt 31 Aug 2019 von guest678. Gefragt 14 Jan 2019 von hApA1996. Wahrscheinlichkeit, dass man mindestens die Augensumme 11 würfelt? Gefragt 28 Okt .Es gibt (4*4-4)/2=6 Ausgänge, bei denen A gewinnt. Die Funktion Zufallszahl und die Darstellung von Diagrammen ermöglichen das Experimentieren.Programmbeschreibung und Beispieldatei. Es kommt hier nicht auf die Reihenfolge der einzelnen Ergebnisse an.
Würfeln mit gezinktem Würfel
Die Wahrscheinlichkeiten der Augenzahlen sind der folgenden . Wenn du mir nicht glaubst, nimm einen Würfel und . Kommentiert 6 Jun 2020 von Gast az0815. würfel; stochastik; unfair + 0 Daumen. Dafür sorgt ein in das Holz eingearbeitetes Metallstück. Zwei 4-seitige, gezinkte Würfel. Eingabetools: LaTeX-Assistent Plotlux Plotter Geozeichner 2D Geoknecht 3D Assistenzrechner weitere .Wahrscheinlichkeit, gezinkter Würfel. Die resultierenden Werte sind: P1 = 0,38125 für 10-seitige Würfel, P2 = 0,3072 für 12-seitige Würfel und.
Python-Beispiel: Die Würfel sind gefallen
Wie groß ist die Wahrscheinlichkeit einer Augensumme von 11?Meine Frage: Hallo leute, ich habe ein Problem und zwar habe ich hier eine Aufgabe zu einem gezinkten Würfel.
4 Beispiel zu Zufallsexperimente und Wahrscheinlichkeit
Den normalen Würfel habe ich mit Math. Beliebte Fragen: Mü und Sigma aus .Baumdiagramm und Summenregel.

Die Berechnung von Wahrscheinlichkeiten bei einfachen Zufallsexperimenten ist leicht zu lernen.Beispiel zu Zufallsexperimente und Wahrscheinlichkeit.Ein 6-seitiger, gezinkter Würfel mit den Augenzahlen 1, 2, 3, 4, 5, 6 wird zweimal .Man geht davon aus, dass es sich bei dem Würfel um einen sogenannten idealen Würfel handelt, bei dem der Schwerpunkt in der Würfelmitte liegt und somit die Wahrscheinlichkeit des Würfelns jeder bestimmten Augenzahl gleich groß ist. Ich habe hier bewusst die Addition genommen, da ja .
- Gewerberegister Österreich Kostenlos
- Gewichteter Mittelwert Excel | gewichtetes Mittel Pivot
- Gigaset N510 Ip Hinter Fritzbox
- Gigaset Sl3 Professional Bedienungsanleitung
- Ghs P304 Erklärung _ GHS
- Gewicht Cannondale Topstone 1 , Cannondale Topstone 1 APEX 2024 28 Zoll
- Gewehr G82 Technische Daten – Wie weit schießt man mit einem Scharfschützengewehr?
- Gewichtskraft Fläche Berechnen
- Giants Software Download Free – Dedicated Server Software
- Gimp Ebene Verschieben Anleitung
- Gewobag Telefonnummer | GEWOBAG Hofgeismar eG
- Gewicht 3 Schichtplatte 27 Mm | 3-Schichtplatten Fichte, A/B online im SCS-Holzshop kaufen
- Gewürzmischungen Rezepte _ Kräutersalze, Gewürzmischungen, & Co