BAHTMZ

Geometrische Reihe Berechnen _ Reihen untersuchen

Di: Samuel

Geometrische Folge

Fur 0 bilden die Reihenglieder keine Nullfolge, daher ist in diesem Fall die Reihe divergent. (00:10) Das geometrische Mittel, auch mittlere Proportionale genannt, ist ein Lagemaß von quantitativen Beobachtungswerten der deskriptiven Statistik.Unendliche Reihen. Berechnen Sie den Wert der unendlichen geometrischen Reihe 1 + 0,8 + 0,64 + .Geometrische Reihen kommen in vielen Bereichen der Mathematik vor, z.Kommen wir zu einem weiteren Beispiel. Rechner für eine unendliche Reihe, die zu einem festen Wert konvergiert. Hier haben wir eine rekursiv definierte Reihe.Aufgaben aus früheren Prüfungen, in denen die geometrische Reihe vorkommt Berechnen Sie . Dieser Artikel steht unter einer freien CC-BY-SA 3. Juni, 2003 – 19:17: Berechnen . Es ist hilfreich, darüber nachzudenken, wie sie eigentlich aussieht.Geometrische Folgen: Hier ist das Verhältnis zwischen aufeinanderfolgenden Gliedern konstant.Ein allgemein gültiges Assoziativ- und Kommutativgesetz für Reihen existiert nicht.

Hiermit ist dann auch automatisch gezeigt, dass die vorliegende Reihe konvergiert: Wenn die Form besitzt, so handelt es sich um eine geometrische Reihe.Inhalt ?In diesem Video lernst du, wie man ganz einfach überprüfen kann, ob eine geometrische Reihe konvergiert oder divergiert. Entfernen von . In unserem Video dazu erklären wir dir, wie du eine geometrische Reihe und ihren Grenzwert berechnen .Anwendung der Geometrischen Summenformel [Bearbeiten] Die geometrische Summenformel lässt sich dazu verwenden, das für eine Rente gesparte Geld zu berechnen. Da es arithmetische und geometrische Folgen gibt, lassen sich auch derartige Reihen erstellen. Hier siehst du eine Reihe in einer allgemeinen Schreibweise: Vielen Dank schonmal im Voraus . Dafür müssen alle Werte aufsummiert werden und nachgeprüft werden, ob die Reihenwerte konvegieren oder nicht.

Online-Rechner: Geometrische Folge

Abgerufen von „https://de.Geometrische Folge berechnenIn diesem Mathe Lernvideo erkläre ich (Susanne) die geometrische Folge und zeige viele Beispiele, in denen man q berechnen und di. Der Reihenrechner überprüft die Konvergenz der Reihen mithilfe von numerischen Methoden. Mathematische Formulierung. Das bestätigt auch die Formel a n =aq n-1. wir betrachten die Reihe P1 k=0 2ka 2k = P1 k=0 2k 1 (2k) = P1 k=0 (21 )k. reihen; summe; geometrische-reihe; partialsumme + 0 Daumen. Der nächste Term besteht also aus dem vorherigen Term multipliziert mit 9/10, also haben wir 10 ⋅ 9/10. Get the free Folgen und Reihen widget for your website, blog, Wordpress, Blogger, or iGoogle. Geben Sie dazu Folgendes vor: Das Start-Folgenglied, welchen (konstanten) Quotienten die Folgenglieder haben sollen, und welcher Teilbereich der geometrischen Folge berechnet werden soll. so entsteht eine Menge mit fraktalem Rand, die sogenannte Koch-Schneeflocke. Das Ergebnis wird mit einer bestimmten Genauigkeit erreicht. +1/4^{n} Gefragt 8 Okt 2019 von Gucki123. Arithmetische Reihen sind im Allgemeinen divergent. Betrachte P1 k=1 1 k . Jedes Glied einer geometrischen Folge ist nämlich das geometrische Mittel seiner Nachbarglieder.Geometrische Reihe Harmonische Reihe e-Reihe Absolute Konvergenz einer Reihe Umordnungssatz für Reihen Cauchy-Produkt für Reihen Aufgaben; Konvergenzkriterien für Reihen Potenzreihen Exponential- und Logarithmusfunktion Trigonometrische und Hyperbolische Funktionen Stetigkeit Ableitung IntegraleAdded Apr 13, 2013 by Math_Man in Mathematics. Wir betrachten zunächst den Fall und damit , da wir nur in diesem Fall die geometrische Summenformel anwenden können. Find more Mathematics widgets in Wolfram|Alpha.Wir leiten uns auf eine sehr einfache Weise die Formel für eine geschlossene Geometrische Reihe her.

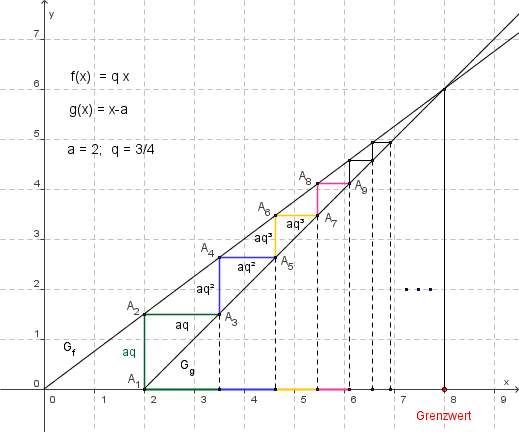
Schreiben Sie die periodische Zahl . q= a n+1 /a n = Das Verhältnis eines Folgengliedes a n+1 zum vorigen Folgenglied a n. Die Bezeichnung „geometrische Folge“ leitet sich aus dem geometrischen Mittel ab. Für erhält man etwa: Den Wert einer Reihe zu bestimmen, kann sehr schwierig sein und lässt sich mit Ausnahme einiger feststehende Ausdrücke in der Regel nicht auf bloßes Einsetzen in eine Formel reduzieren. In diesem Einführungsvideo . Die geometrische Reihe ist eine Summe über einen Quotienten q und hat im Allgemeinen die Form. Das -te Glied einer . Abhängig von der Größe von q bevorzugt man einer der zwei folgenden gleichwertigen Fomeln: Wert berechnen: Falls eine geometrische Reihe oder Teleskopreihe vorliegt, kannst du den Wert der Reihe berechnen.

Harmonische Reihe • einfach erklärt · [mit Video]

Berechne die Summe dieser geometrischen Reihe: 1 + 1/4 + 1/16 + . in der Wahrscheinlichkeitsrechnung oder Finanzmathematik. 10-0 – 10-3 + 10-6 – 10-9 + – .Kommt dann nicht immer eine unendlich große Zahl heraus, wenn man unendlich viele Zahlen addiert? Bei Reihen beschäftigt man sich also damit, ob das Ergebnis einer Reihe ein endlicher Wert ist oder – anders ausgedrückt – ob die Reihe konvergiert. Dazu schauen w. Eine geometrische Folge ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass das Verhältnis zweier benachbarter Folgenglieder konstant ist. Wie man sieht, ist die gegebene Folge eine geometrische Folge mit q=3 und a 1 =1 .Auch für geometrische Folgen lassen sich Partialsummen berechnen. Zudem erfährst du, wie man .2020, 16:10: Gehebrim: Auf diesen Beitrag antworten » Ich erstelle abschließend eine Zusammenfassung von dem was ich durch eure Antworten verstanden habe: Formel Summe geometrische Formel: Sn = a1*(q^n-1)/(q-1) Berechnung von q: . Erster bekannter Term-Index.Geometrische Folge.php?title=Formelsammlung_Mathematik:_Unendliche_Reihen:_Geometrische_Reihe&oldid=911362“Geometrisches Mittel einfach erklärt. Klicken Sie dann auf Berechnen. Es interessieren deshalb vor allem die Partialsummen, die auch als endliche arithmetische . Nach der Definition gilt dann: s_n=\sum\limits_ {k=1}^n a_k sn = k=1∑n ak.Mit der geometrischen Reihe verwandt sind die Potenzreihen = = .

Bearbeitete Beispiele: Endliche geometrische Reihen

Eine Umordnung einer Reihe wird durch eine Permutation ihrer Indexmenge dargestellt. Beispiel: Es ist die Summe s 10 der Folge (1) zu berechnen.Kommen wir zur geometrischen Reihe . 17 [Wert der Beta-Funktion] 18 Iterierter Differenzenoperator. Für die n-te Partialsumme s n einer geometrischer Folgen gilt: s n = a 1 ⋅ q n − 1 q − 1. Korollar zum Binomischem Lehrsatz.Wenn du noch nicht ganz verstehst, was eine geometrische Folge ist, sei nicht frustriert! Wir erklären dir, was das bedeutet und . Folgen & Reihen. Gegeben: a 1 = 2; q = 3 Gesucht: s 10 Lösung: s 10 = 2 ⋅ 3 10 − 1 3 − 1 = 3 10 − 1 = 59 048 16 Leibniz-Regel.

Geometrisches Mittel

Man kann konvergente Reihen unter Beibehaltung ihres Wertes dann und nur dann beliebig .Eine arithmetische Reihe ist die Folge, deren Glieder die Summe der ersten Glieder (den Partialsummen) einer arithmetischen Folge sind. Mit der geometrischen Summenformel. Das n-te Glied a n einer geometrischen Folge mit dem Anfangsglied a und dem Quotienten q berechnet sich aus : a 1 = a, a 2 = aq, a 3 = aq 2, a 4 = aq 3, .

Setzt man die Summenbildung ins Unendliche fort, spricht man von einer .Geometrische Reihen kommen in sehr vielen Anwendungen immer wieder mal vor, daher ist es sehr wichtig zu wissen, wie man diese berechnen kann. Gegeben sei die folgende Folge: Gesucht ist das 6.

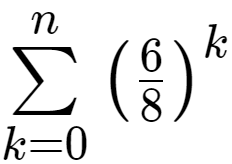
Ermittel einen Term anhand zwei anderen Termen. Bei endlichen Summen kommt es nicht auf die Reihenfolge der Summanden an, man darf sie also nach Belieben umordnen und ebenso nach Belieben darf man Klammern setzen und entfernen: Nicht aber bei unendlichen Summen, denn das Setzen bzw. die Folge der Partialsummen konvergiert) , und sie wird mit der Formel lim n → ∞ S n = b 1 1 − q berechnet. 11 Korollar zu den Partialsummen der geometrischen Reihe. Bekannter Term-Index. Ermittel einen Term anhand eines anderen Term und dem gemeinsamen Verhältnis.

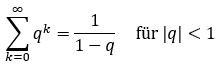
entspricht der Summe einer Folge an verschiedenen Werten eines Intervalls.Geometrische Reihe – Grenzwert berechnen bei verschobenem Start, k=1 oder k=2Die normale geometrische Reihe beginnt bei k=0 mit ihrer Lösungsformel. Folgen werden häufig mit Reihen verwechselt. Die Reihe ist eine Summe mit dem Startwert 0 und theoretisch unendlich vielen Schritten.

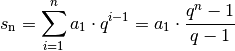
Links wird die geometrische Folge mit q=(1/2)sqrt(2) graphisch dargestellt. Die geometrische Reihe ist die Reihe von und ihr Grenzwert ist . Eine arithmetische Reihe summiert dann die Glieder der dazugehörigen arithmetischen Folge auf. zur Stelle im Video springen. Glied der zugehörigen Reihe.Berechnen Sie das Cauchy-Produkt einer geometrischen Reihe mit sich und leiten Sie daraus eine Formel für die abgeleitete geometrische Reihe ∑ ∞k=1 kq k-1 mit q ∈ ℂ, |q| < 1 her.Die geometrische Reihe konvergiert genau, dann wenn . Wert des ersten bekannten Terms.Eine bekannte Reihe ist die geometrische Reihe . Die Summierung der Folgenglieder ergibt die geometrische Reihe.Wir können Taylorreihen berechnen, um zu verstehen, wo der Grenzwert der geometrischen Reihe herkommt. Der erste Term ist 10, und der zweite Term a_2 = a_1 ⋅ 9/10.

Geometrische Reihen online lernen

unter Angabe der verwendeten Formel! Stellen Sie als Bruch dar: 10-0 + 10-3 + 10-6 + 10-9 + .10 Partialsummen der geometrischen Reihe. Zweiter bekannter Term-Index.0 oder einer dazu kompatiblen . Wenn du dich auf eine Mathe Prüfung vorbereiten musst, d. geometrische; reihe; summenformel; komplexe-zahlen; bruch; Gefragt 22 . Dieses Aufsummieren kann direkt geschehen, indem man die Glieder addiert. Geometrische Folge ist eine Sequenz von Zahlen, wo jeder Term nach dem ersten durch das Multiplizieren des vorherigen Terms mit einer fixen nicht-Null Zahl, das sogenannte gemeinsame Verhältnis, ermittelt wird. Ist die Indexmenge zum Beispiel die Menge der natürlichen Zahlen mit Null und :, eine bijektive Abbildung der natürlichen Zahlen auf sich, so heißt = eine Umordnung der Reihe =. Jetzt versuch ich Folgendes herauszubekommen (Ansätze funktionieren nicht):

Reihenkonvergenz und

Geometrische Folgen und Reihen

Mit diesem Online-Rechner können Sie geometrische Folgen berechnen.2020, 15:10: mYthos: Auf diesen Beitrag antworten » Nein.

Geometrische FOLGE berechnen

läßt sich der Grenzwert explizit berechnen: für . wäre schön wenn es jemand gibt der den Rechenweg step für step aufschreiben könnte.Namensherkunft.Kannst du das Gegenteil zeigen, also so divergiert die Reihe sofort.Mathematische Reihen.Eine geometrische Folge ist eine Folge von Zahlen, bei der alle Zahlen bis auf die erste durch Multiplikation der vorhergehenden Zahl mit einem festen Wert ungleich Null, dem Quotienten, berechnet werden. Wir erhalten: Die geometrische Reihe konvergiert also genau dann, wenn die Folge konvergiert. Damit kannst du ihn frei verwenden, bearbeiten und weiterverbreiten, solange du „Mathe für Nicht-Freaks “ als Quelle nennst und deine Änderungen am Text unter derselben CC-BY-SA 3. Also bestimmen wir die Taylorreihe der Funktion . 12 Binomischer Lehrsatz. partialsumme; reihen; summe + 0 . Send feedback | Visit Wolfram|Alpha. Für ist diese Reihe (absolut) konvergent, der zugehörige Reihenwert ist . Hier wird ein Wert der Reihe als . Sei (a_n) (an) eine Zahlenfolge, dann heißt die Folge der Partialsummen s_1=a_1 s1 = a1, s_2=s_1+a_2 s2 = s1 + a2, allgemein: s_n=s_ {n-1}+a_n sn = sn−1 + an eine Reihe.

Arithmetische Reihen sind spezielle mathematische Reihen.

Geometrische Folge

Reihenrechner

Folgen sind Listen von Zahlen, die nach einer bestimmten Regel gebildet .

Aufgaben zu Reihen

Reihe berechnen.Geometrische Reihe.Die zugehörige geometrische Zahlenreihe s n entsteht durch Summation der Zahlenwerte. Dieser Online-Rechner berechnet den n-te Term und die Summe einer geometrischen Folge. n s n = ∑ a k: k = von n = bis n ≤ in -er Schritten. Die -te Schneeflocke hat Kanten.

Reihen untersuchen

Ein Beispiel ist , mit einem konstanten Verhältnis von 2. Autor: Beitrag ilona (una) Neues Mitglied Benutzername: una Nummer des Beitrags: 3 Registriert: 06-2003: Veröffentlicht am Freitag, den 13.

Potenzreihen

Neben der harmonischen Reihe gibts es noch einige andere bekannte Funktionenreihen, die du kennen solltest. Mit dieser Formel können wir die Partialsumme explizit berechnen.Dies ist meines Erachtens eine geometrische Reihe. Das Ergebnis zeigt die Folgenglieder der .

Komplexe geometrische Reihe berechnen

Widget zur Veranschaulichung von Folgen und Reihen und ihrer Konvergenz oder Divergenz.Wenn der Nenner q der geometrischen Folge (b n) die Ungleichung q < 1 erfüllt, dann gibt es eine Summe S der Folge (dh.Grundlage für eine arithmetische Reihe ist eine arithmetische Folge, also eine Folge von Zahlen mit konstantem Abstand wie etwa die Zahlen 2, 5, 8 und 11 mit dem Abstand 3. Die Summe der natürlichen ganzen Zahlen stellt eine unendliche .

Rechenregeln für Reihen

Die geometrische Reihe.Ich habe bereits nach so einer frage gesucht aber entweder nichts ähnliches gefunden oder ich hab die rechenschritte nicht nachvollziehen können.berechnet sich nach folgender Formel: a 1 = Das erste Glied der zugehörigen Folge. Bei einer mathematischen Reihe sind die Glieder der zugrunde liegenden mathematischen Folge über Rechenzeichen miteinander verbunden. Letzter addierter Summand: . Folgen haben Glieder, keine Ziffern. Wir erinnern uns an die Definition der Taylor-Reihe:geometrische Reihe: ZahlReich – Mathematik Hausaufgabenhilfe » Klassen 8-10 » Arithmetik » geometrische Reihe « Zurück Vor » Das Archiv für dieses Kapitel findest Du hier.Numerische Berechnung von Reihen a k = Folge der Partialsummen. Dies ist aber eine geometrische Reihe, die . Bekannter Term-Wert. Arithmetische Reihe. Auch von meiner ursprünglichen Vermutung, dass der Grenzwert 0 ist, bin ich abgerückt, mit diversen unerlaubten Hilfsmitteln habe ich herausbekommen, dass der Grenzwert 2/3 ist. Stell dir dazu vor, du würdest jedes Jahr 2000 € {\displaystyle 2000\,\mathrm {\euro} } für deine Rente sparen, die mit 5 % {\displaystyle 5\,\%} verzinst werden. Partialsumme bestimmen und damit Summenwert berechnen (Reihe) Gefragt 9 Apr 2021 von Zeppi.Rechner für Geometrische Reihen. Je höher die Genauigkeit, desto größer ist der Rechenaufwand. Man erkennt, dass die Glieder der Folge immer kleiner werden und sich Null immer mehr nähern. Da sich die Kantenlänge in jedem Schritt um einen Faktor . Der Reihenrechner berechnet im Augenblick den . Die allgemeine Formel ist , wobei r das konstante Verhältnis ist. Fur >0 bilden die Reihenglieder eine monoton fallende Nullfolge, sodass der Verdichtungssatz anwendbar ist, d. Bei der geometrischen Zahlenreihe ist der Quotient q zweier aufeinander folgender Glieder konstant. Man erhält ihn durch die Berechnung der n-ten Wurzel aus dem Produkt der betrachteten positiven Zahlenwerte.

• Gerichtliche Kontrolle Verwaltungsvorschriften
• Geolino Mini | GEOLINO-Wunschabo bestellen
• Geriatrische Versorgung Vorlage
• Genua Gebrauchtsegel , Varianta, Gebrauchte Boote und Bootszubehör
• Genderstudien Deutschland : Was Gendern bringt
• Geometric Deep Learning Definition
• Geometrischer Zugang Kurve | Formen
• German Telephone Numbers : telephone number
• Geringfügige Beschäftigung Bei Steuererklärung Angeben
• Geradezugrepetierer Vergleich : Schnelle Italienerin