Directed Graph Adjacency Matrix

Di: Samuel

Adjacency Matrix.

Matrix Representation of Graphs

This matrix contains all the same information as the graph diagram but in a different form. Adjacency list.

The change process of the weighted directed graph and adjacency matrix ...

The rows and columns are ordered according to the nodes in nodelist. Example: Consider the following graph.For example, graphs in which either the in-degree or out-degree is bounded by a constant are sparse.In contrast when we use the same adjacency matrix to create a directed graph, only the edge from node 3 to node 0 is added, no edge is added in the opposite direction from node 0 to 3. Because a DAG cannot have self-loops, its adjacency . Possible values: upper: the upper right triangle of the matrix is used, lower: the lower left triangle of the matrix is used.Graph representation. If it is a character constant then for every non-zero matrix entry an edge is created and the value of the entry is added as an edge attribute named by the weighted argument. Example: Consider the .We can represent an unweighted graph with an adjacency matrix.

What Is the Difference Between a Directed and an Undirected Graph

When implementing graphs, you can switch between these types of representations at your leisure.In particular, a graph with only O(V) edges is said to be sparse.DiGraph(X>0) nx. To detect a back edge, we need to keep track of the nodes visited till now and the nodes that are in the . the vertex corresponding to the first row will be vertex 0 in the graph, etc. If None, then each edge has weight 1. Let’s consider a directed graph G that consists of n nodes. A graph is often represented by a graph diagram like the one on the left, below: The same graph can be represented as an adjacency matrix like the one on the right.Both the adjacency matrix and the adjacency list can be used to store directed or undirected graphs. For the current . An Adjacency List is used for representing graphs.Assigning 1 to all that there is directed edge from to and to the other entries we obtain the vertex matrix.Adjacency can’t take an np.Print Adjacency List for a Directed Graph. The adjacency matrix is often also referred to as a connection matrix or a vertex matrix. The adjacency matrix of the graph G is matrix A of order n × n, where A = [a_ij] and defined by, For example: Let’s consider a directed graph as shown below and construct its adjacency .

Graph Representation using Adjacency Matrix

adjacency-list representation of a directed graph

If you want to see it now, look at the third lecture from my notes from 2009.For logical adjacency matrices, the graph has no edge weights.Martin McBride. Adjacency matrix. It is ignored for directed graphs. It’s typically the kind of matrix you get when calculating the correlation between each pair of individual.A directed graph, as well as an undirected graph, can be constructed using the concept of adjacency matrices.java implements the digraph API using the adjacency-lists representation. If the graph has no edge weights, then A(i,j) is set to 1. Adjacency Matrix of an Undirected Graph. Each edge of an undirected graph connecting Vertices \(u\) and \(v\) is represented by two directed edges: one from \(u\) to \(v\) and one from \(v\) to \(u\). It is a part of Class 12 Maths and can be defined as a matrix containing rows and columns that are generally used to represent a simple .DSA Full Course: https: https:/.V;E/, the adjacency matrix A G Dfaijgis deﬁned so that aijD (1 if i!j2E 0 otherwise. Incidence Matrix Representation: If a directed graph G consists of n vertices and m edges, then the incidence matrix is an n x m matrix C = [c ij] and defined by.

Graph with directed edges

Let us consider the following undirected graph and construct the adjacency matrix −.both: the whole matrix is used, a symmetric matrix is returned. Adjacency Matrix Representation of Graph.A = adjacency(G,’weighted‘) returns a weighted adjacency matrix, where for each edge (i,j), the value A(i,j) contains the weight of the edge.

Directed graph: checking for cycle in adjacency matrix

Graph Data Structures (Adjacency Matrix, Adjacency List

We observe that the adjacency matrix of any undirected multigraph is symmetric. For a simple graph, with no self-edges, elements on main diagonal are 0 3. I think there is not another way to implement your graph in networkx because the mixed graph are not allowed, as mentioned here: – Is it possible to add undirected and directed edges to a graph object . a) Find the vertex matrix M of the following graph.In igraph you can use igraph. The adjacency matrix for the new graph would be: Explanation: As you can see, the graph now contains directions.The space required by the adjacency matrix representation is O(V 2), so adjacency matrices can waste a lot of space if the number of edges |E| is much smaller than O(V 2). adj[i][j] == 1. For large graphs, the adjacency matrix contains many zeros and is typically a sparse matrix. The adjacency matrix of a graph G is a square-matrix of 0’s and 1’s with a row for every vertex. graph_from_adjacency_matrix() operates in two main modes, depending on the weighted argument. In other words, you can determine the number of length k k walks between any pair of vertices simply by computing the k k th power of the adjacency matrix! That may seem amazing, but the proof uncovers this simple relationship between . The graph diagram is usually easier to visualise, but .

Graph Representation: Adjacency List and Matrix

If None, then the NumPy default is used.In this video we will learn about directed graph and their representation using adjacency matrix. In this guide, we’ll cover all of them. Problem: Given the adjacency list and number of vertices and edges of a graph, the task is to represent the adjacency list for a .In this video, I have explained the two most popular methods(Adjacency Matrix and Adjacency List) for representing the Graph.draw_kamada_kawai(G, with_labels=True) In this way you have that undirected edges are bidirectional connection.For the graph above, the adjacency matrix looks like this: Since there’s an edge going from node 1 to 2, we see a 1 in both (row 1, column 2) and (row 2, column 1).Here, we will be discussing adjacency matrix representation for directed graphs.To store the adjacency list, we need O(V + E) O ( V + E) space as we need to store every vertex and their neighbors (edges).

Graphs and graph representations

adjacency

As we proceed to show, adjacency matrices can be used to compute number of walks in a graph.If a graph has n vertices, we use n x n matrix to represent the graph.

Convert a graph to an adjacency matrix — as

A NetworkX graph. For this syntax, G must be a simple graph such that ismultigraph(G) returns false.The adjacency matrix of a graph is a matrix where all row and columns represent the set of vertices belonging to that graph. If we have a directed edge e: . It’s often represented as a two-dimensional array in computer programs. Directed graphs have adjacency matrices just like undirected graphs. The lack of directionality in the graph results in a symmetric matrix.This Demonstration uses the Floyd–Warshall algorithm to find the shortest-path adjacency matrix and graph.To create a directed Graph with an adjacency matrix, we must decide which vertices the edges go from and to, by inserting the value at the correct indexes (i,j). To represent a weighted Graph we can put other values than ‚1‘ inside the adjacency matrix. We can easily represent the graphs using the following ways, 1. This will alter the matrix since nodes are connected only in a specific direction.

6 Directed Graphs

At any step in the algorithm, the -entry in the adjacency .Graphs in Python can be represented in several different ways.

Adjacency Matrix & List

Struktur Data Graf (Matriks Adjacency, Daftar Adjacency

The edge data key used to provide each value in the matrix.An adjacency matrix is a square matrix where individuals in rows and columns are the same.In a directed graph, some of the terminologies mentioned earlier have small adjustments. If , then there’s no edge between the two nodes.Unlike the case of directed graphs, the entries in the incidence matrix of a graph (undirected) are nonnegative. The notion of adjacency matrix is basically the same for directed or undirected graphs. The desired data-type for the array. By default, we get an unweighted and oriented network. DiGraph (adjacency_matrix, nodetype = int) G. The length-k counting matrix of a digraph, G G, is (AG)k ( A G) k, for all k ∈ N k ∈ N. Adjacency matrix of the above undirected graph will be − The order of the vertices are preserved, i. That’s because there are no edges from any node .from_pandas_adjacency(df, create_using=networkx. We now can add directions to the previous graph, then see how that affects the matrix. In this example, we have 1 connection from E to C, and 2 connections from C to E. Also notice that the diagonal consists entirely of zeros.To construct an undirected graph using only the upper or lower triangle of the adjacency matrix, use graph(A,’upper‘) or graph(A,’lower‘). The graph to convert. In the case of a directed graph GD. This, together with the simple graph constraint earlier, limit the number of undirected/directed edges to be 45/90, respectively.array as argument, but that is easily solved . In the adjacency matrix, all rows indicate a tail or a start of a potential edge, while the columns indicate the head or target of that edge: The cells in an adjacency matrix can have a value of 1 or 0 according to . edges [(0, 1), (0, 2), (1, 0), (1, 3), (2, 0), (3, 0), (3, 1)] Creating a graph from an edge list .Arguments graph.To find cycle in a directed graph we can use the Depth First Traversal (DFS) technique. The algorithm is visualized by evolving the initial directed graph to a complete digraph in which the edge weight from vertex to vertex is the weight of the shortest path from to in the initial graph. It is based on the idea that there is a cycle in a graph only if there is a back edge [i.Chapter 6 Directed Graphs b d c e Figure 6. Note that these need not even be diagonalizable! We will defer a discussion of the general theory until we discuss directed graphs, which will happen towards the end of the semester. Here, for every vertex in the graph, we have a list of all the other vertices which the particular vertex has an edge to.more, and it can be applied to adjacency matrices of strongly connected directed graphs. It’s an matrix consisting of zeros and ones, where is the number of nodes. First of all, we’ll quickly recap graph theory, then explain . The location of each nonzero entry in A specifies an edge for the graph, and the weight of the edge is equal to the value of the entry. However, this is not always the case for the adjacency matrix of a directed multigraph. Here is an example of the two representations on an undirected graph. adj[i][j] == 0 . The sum of the lengths of all the adjacency lists in Adj is |E|.The adjacency matrix of the directed graphs is as follows: 2. → All example graphs can . Thus the time to compute the out-degree of every vertex is Θ (V + E) In-degree of each vertex.There are some things to be aware of when a weighted adjacency matrix is used and stored in a np. It is symmetric (!=!#) 2. Maybe I can multiply matrix A by itself n times, and check if there is non-zero diagonal in each resulting matrix. The number of ones in an incidence matrix is equal to the number of edges in the graph.For a directed graph, if there is an edge between V x to V y, then the value of A[V x][V y]=1, otherwise the value will be zero. Note: : It can be proved that if M is the vertex matrix of a digraph, then the entry will show the number of r-step connections from to .The adjacency matrix for a graph is n X n and each element contains 0 for non-neighbors and the edge weight for neighbors.A graph is made up of vertices/nodes and edges/lines that connect those vertices.if there is an edge from vertex i to j, mark adj[i][j] as 1.

stoimen's web log

Adjacency Matrix Representation of Graph

If the graph is not simple, then the matrix element for a node with a self-edge is .Directed acyclic graphs are sometimes instead called acyclic directed graphs or acyclic digraphs.If it is NULL then an unweighted graph is created and the elements of the adjacency matrix gives the number of edges between the vertices. We use the adjacency-lists representation, where we maintain a vertex-indexed array of lists of the vertices connected by an edge to each vertex.

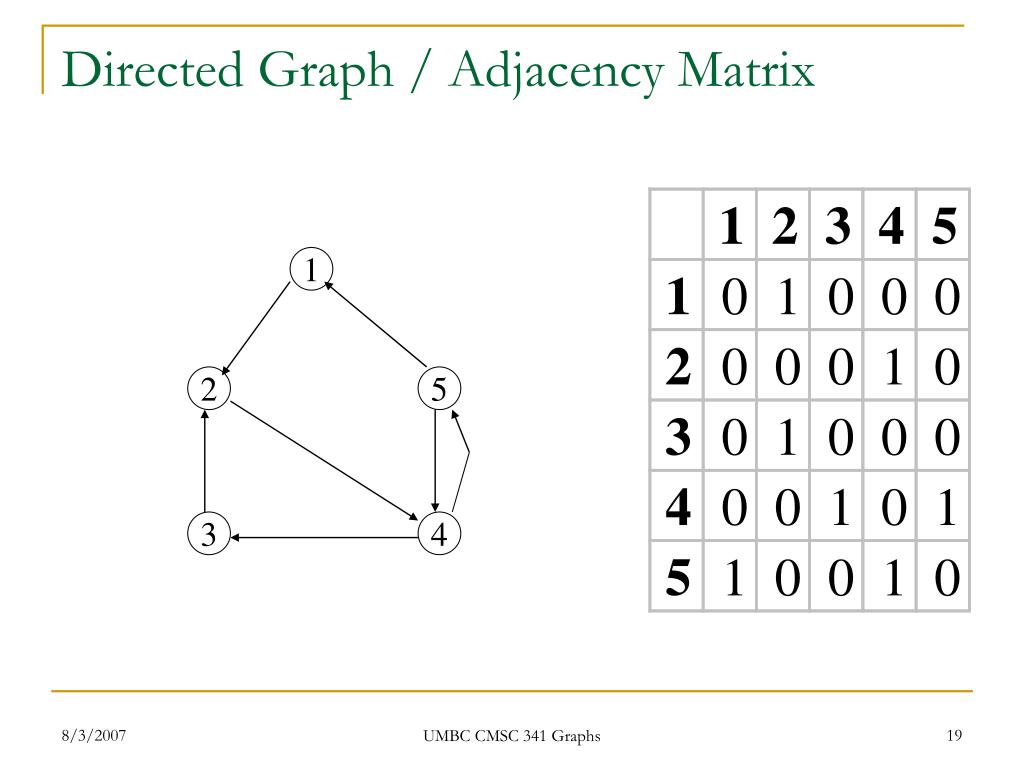
PPT - CMSC 341 PowerPoint Presentation, free download - ID:786652

For nonlogical adjacency matrices, the graph has edge weights. Graph out-degree of a vertex u is equal to the length of Adj [u].There is an alternative method respect to the DFS algorithm to check if there are cycles in a directed graph represented with an adjacency matrix? I found piecemeal information on the properties of matrices. Gives how to create the adjacency matrix for undirected graphs. The only difference is that the adjacency matrix for a directed graph is ., a node points to one of its ancestors] present in the graph. We usually write B instead of B(G).DiGraph()) However, what ends up happening is that the graph object either: (For option A) basically just takes one of the values among the two parallel edges between any two given nodes, and deletes the other one .

Adjacency matrix (vertex matrix)

If its element is 1, that means that there’s an edge between the -th and -th nodes. The most notable ones are adjacency matrices, adjacency lists, and lists of edges.Graphs Adjacency Matrix and Adjacency List Special Graphs Depth-First and Breadth-First Search Topological Sort Eulerian Circuit Minimum Spanning Tree (MST) Strongly Connected Components (SCC) Depth-First and Breadth-First Search 16. Adjacency-list representation of a directed graph: Out-degree of each vertex.Adjacency to create a graph from an adjacency matrix without having to use zip.

Graph Representation with an Adjacency Matrix

The in-degree of a vertex u is equal .java implements the same API using the adjacency-matrix . For example, if A(2,1) = 10, then G contains an edge from node 2 to node 1 with a weight of .Adjacency Matrix of a Directed Graph For a directed graph, if there is a directed edge between two vertices, then the value is considered to be 1, else it is considered to be 0.How do we represent graphs using adjacency matrices? That is the subject of today’s graph theory lesson! We will take a graph and use an adjacency matrix to .if there is no edge from vertex i to j, mark adj[i][j] as 0.

Adjacency Matrix -- from Wolfram MathWorld

we will take a graph with 5 nodes and then we will create a. To find if a vertex has a neighbor, we need to go through the linked list of the vertex. If nodelist is None, then the ordering is produced by G.

Graphs | CodePath Guides Cliffnotes

(as the Adjacency Matrix of this graph will already contain 10×10 = 100 cells). When you use digraph to create a directed graph, the adjacency matrix does not need to be symmetric. The proof is bijective: a matrix A is an adjacency matrix of a DAG if and only if A + I is a (0,1) matrix with all eigenvalues positive, where I denotes the identity matrix. A = Properties of the Adjacency Matrix 1.Case 2: Unweighted, directed graph. Below is a directed and weighted Graph with the Adjacency Matrix representation next to it . For example, in row 1 .A graph may be undirected (meaning that there is no distinction between the two vertices associated with each bidirectional edge) or a graph may be directed (meaning that its edges are directed from one vertex to another but not necessarily in the other direction).

Use an adjacency matrix to find the number of directed walks of length ...

(In weighted graphs, if A is numeric valued, then A [u] [v] would be the weight of the . A = adjacency(G,weights) returns a weighted adjacency matrix . A [u] [v] is 1 if there is an edge from u to v, otherwise it is 0. Graph Traversal The most basic graph algorithm that visits nodes of a graph in certain order Used as a .

Detect Cycle in a Directed Graph

Undirected graph with no loops and no multi-edges. Let G be a graph (directed or undirected) on [n] with adjacency .2 A 4-node directed graph with 6 edges. To represent this graph as the adjacency matrix A, we’ll let the indices of the rows and columns represent nodes, or vertices. If this argument is NULL then an unweighted graph is created and an element of the adjacency matrix gives the number of edges to . This is how the adjacency matrix of the above roadmap graph would . AdjMatrixDigraph.

BAHTMZ

General