Differentiation Rules Examples
Di: Samuel
Recall that the definition of derivative is: Given any number \(x\) for which the limit
Derivative rules review (article)
It can be used on its own, or in combination with other methods. It also provides examples and exercises to practice basic differentiation. For example, it allows us to find the rate of change of velocity with respect to time (which is acceleration). As we will quickly see, each derivative rule is necessary and useful for finding the instantaneous rate of change of various functions. Constant Rule: If f (x) = c, where c is a constant, then the derivative is zero: f‘ (x) = 0.In this section we explore the relationship between the derivative of a function and the derivative of its inverse.
Derivative Rules Sheet
The derivative of a constant is always 0, and we can pull out a scalar constant when taking the derivative. Full 1 Hour 35 Minute Video: https://www. 1 – Derivative of a constant function.6 Example Find the derivative of f(x) = cotx x. Past papers Textbooks. Integral calculus involves integration which is the reverse process of differentiation.Constant rule, difference rule, sum rule, power rule, etc.where the vertical bars denote the absolute value.
Calculus I
2) lim Δ x → 0 e Δ x − 1 Δ x = 1. Furthermore, we can continue to take derivatives to obtain the third derivative, fourth . Example • Bring the existing power down and use it to multiply.The instantaneous rate of change of a function with respect to another quantity is called differentiation.Power Rule for Differentiation In this section we learn how to differentiate, find the derivative of, any power of \(x\). There are two types of differential calculus equations – ordinary and partial differential equations.To do the chain rule you first take the derivative of the outside as if you would normally (disregarding the inner parts), then you add the inside back into the derivative of the outside.Summary of the quotient rule.3 : Differentiation Formulas. The product rule is the method used to differentiate the product of two functions, that’s two functions being multiplied by one another .
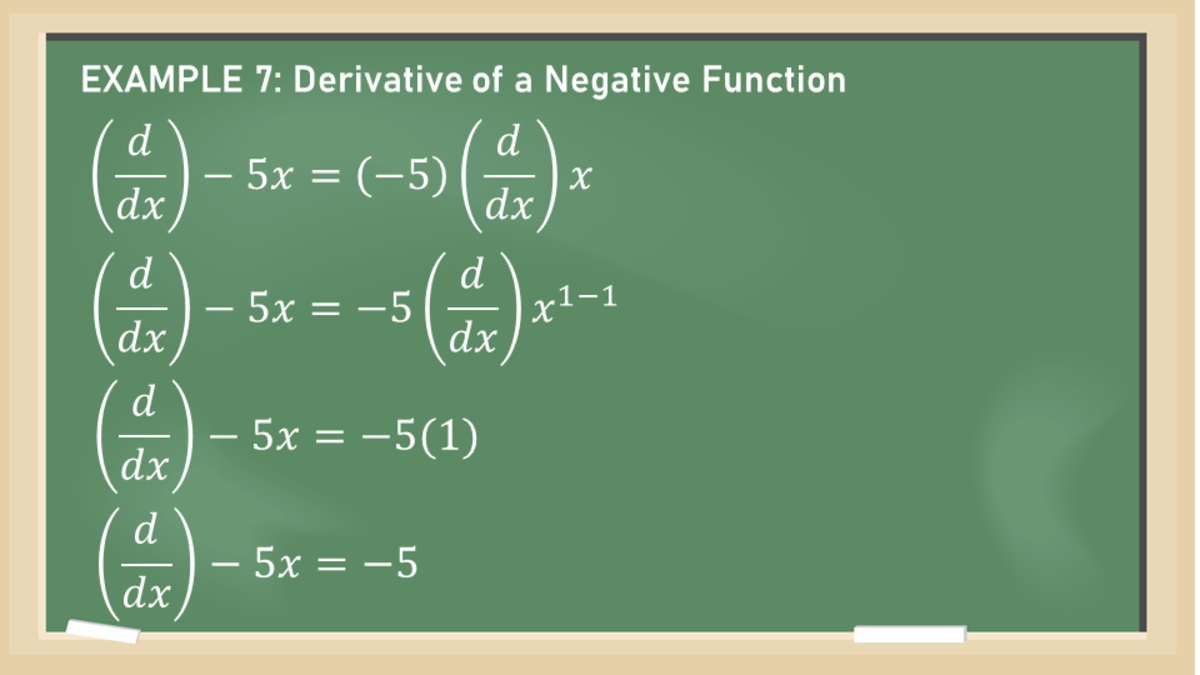
Exponential Functions: If f (x) = e x, then:Multiple notations for the derivative exist. The derivative of at can be denoted ′ (), read as prime of ; or it can be denoted (), read as the derivative of with .3 Derivative Rules ¶ Using the definition of the derivative of a function is quite tedious.First differentiate the first term in the sum, 10×3 10 x 3 using the power rule: dy dx =30×2 d y d x = 30 x 2 Now differentiate the second term, 2x 2 x using the power rule again: dy dx =2 d y d x = 2 Adding these derivatives together give us the derivative of y = 10×3 +2x y = 10 x 3 + 2 x: dy dx = 30×2 +2 d y d x = 30 x 2 + 2.
![[大學Math for Econ] Introduction to derivatives - Sum Rule - YouTube](https://i.ytimg.com/vi/BgP0uLYTvEE/maxresdefault.jpg)
The former states that d/dx x^n = n*x^n-1, and the latter states that when you have a function such as the one you have described, the answer would be the derivative of x^2 multiplied by x^3 + 1, then you subtract x^2 multiplied by the derivative of x^3 – 1, and then divide all that by (x^3 – 1)^2. Find the derivative of the polynomial function, f ( x) = 4 x 3 – 5 x 2 + 6 x – 1.3 Rules for differentiation . For learners and parents For teachers and schools. Taking derivatives of functions follows several basic rules: multiplication by a constant: . Solution Since cotx xmeans (cot )x, this is a case where neither base nor exponent is constant, so logarithmic di erentiation is required:Once we recognize the pattern of derivatives, we can find any higher-order derivative by determining the step in the pattern to which it corresponds. The basic rules of Differentiation of functions in calculus are presented along with several examples . For example, speed is the rate of change of displacement at a certain time. The following examples will use the product rule and chain rule in addition to the quotient rule; refer to the product or chain rule pages for more information on the rules.For example, the derivative of a position function is the rate of change of position, or velocity.

1: Constant, Identity, and Power Rules.

In this section, we study . Constant Rule: f(x) = c then f0(x) = 0.
Sum and Difference Rule of Derivatives
As you already know, fundamental lesson content should cover the standards of learning set by the school district or state educational standards.Example: what is the derivative of cos(x)sin(x) ? We get a wrong answer if we try to multiply the derivative of cos(x) by the derivative of sin(x) . [ citation needed ] Logarithms can be used to remove exponents, convert products into sums, and convert division into subtraction — each of which may lead to a simplified expression for . It also allows us to find the rate of change of x with respect to y, which on a graph of y against x is the gradient of the curve.com/MathScienceTutor. Explore step-by-step examples and explanations for various functions. Now that we’ve learned the important derivative rules and the process of differentiating complex expressions, it’s time for us to apply what we’ve learned by working on the functions shown below. ds dt = −4 ×2.According to Tomlinson, teachers can differentiate instruction through four ways: 1) content, 2) process, 3) product, and 4) learning environment. It is a rule that states that the derivative of a quotient of two functions is equal to the function in the denominator g(x) multiplied by the derivative of the numerator f(x) subtracted from the numerator f(x) multiplied by the derivative of the . For each calculated derivative, the LaTeX representations of the resulting mathematical expressions are tagged in the HTML code so that highlighting is possible. To derive each of the functions or each of the terms, we use the power rule, \frac {d} {dx} (x^n) = nx^ {n-1} dxd (xn) = nxn−1 . Notation Shrink towards . When you tell someone you have studied calculus, this is the one skill they will expect you to have. For example, if we have the differential equation \(y′=2x\), then \(y(3)=7\) is an initial value, and when taken together, these equations form an initial-value problem.This calculus 1 video tutorial provides a basic introduction into derivatives.
Power Rule for Differentiation
The quotient rule is a very useful formula for deriving quotients of functions.
Quotient Rule
Note that the quotient rule, like the product rule, chain rule, and others, is simply a method of differentiation.Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals.Implicit Differentiation allows us to extend the Power Rule to rational powers, as shown below. As you might guess from our two examples, e e is closer to 3 than to 2, and in fact e ≈ 2. For instance, finding the derivative of the function below would be incredibly difficult if we were differentiating directly, but if we apply our steps for logarithmic differentiation, then the process becomes much . limΔx→0 eΔx − 1 Δx = 1. If y = f (x) is a differentiable function of x, then dy/dx = f‘ (x) = lim Δx→0 f . ! Instead we use the Product Rule as explained on the Derivative Rules page. Answer ds dt = antn−1= −10t−5. In its simplest form, called the Leibniz integral rule, differentiation .This is an example of the (ε, δ)-definition of limit.Differentiation of a general power multiplied by a constant. This is a very algebraic section, and you should get lots of practice. Because the slope of the tangent line to a curve is the derivative, you find that y ′ = −6 x ; hence, at (−1,9), y ′ = 6, and the tangent line has slope 6 at the point (−1,9).Combining Differentiation Rules.
Basic Differentiation
Below is a list of all the derivative rules we went over in class. As we have seen throughout the examples in this section, it seldom happens that we are called on to apply just one differentiation rule to find the derivative of a given function.Somewhere between a = 2 a = 2 and a = 3 a = 3 the limit will be exactly 1; the value at which this happens is called e e, so that. The new function obtained by differentiating the derivative is called the second derivative. For example, we would like to apply shortcuts to differentiate a function such as \ (g (x) = 4x^7 – \sin (x) + 3e^x\)
Product Rule for Differentiation
Get ready to ace your calculus with these essential differentiation rules. Constant Multiple Rule: g(x) = c · f(x) then g0(x) = c · f0(x) Power Rule: f(x) = xn then f0(x) = nxn−1. • Reduce the old power by one and use this as the new power.The sum and difference rule of derivatives allows us to find the derivative of functions like the following: In this case, its derivative is equal to: This applies to the sum or difference of any number of functions. Mathematics Grade 7 Mathematics Grade 8 Mathematics Grade 9 Mathematics Grade 10 Mathematics Grade .Differentiation rules are formulae that allow us to find the derivatives of functions quickly.This calculus video tutorial explains how to find derivatives using the chain rule. Sum and Difference Rule: h(x) = f(x)±g(x) then h0(x) = f0(x)±g0(x)The power rule will help you with that, and so will the quotient rule.Example 7: Find the slope of the tangent line to the curve y = 12 − 3 x 2 at the point (−1,9). The power rule is a fantastic shortcut for finding the derivatives of basic polynomials. To differentiate s = atnfor any value of n where a is a constant. Afterwards, you take the derivative of the inside part and multiply that with the part you found previously. In this section we introduce a number of different shortcuts that can be used to compute the derivative.Logarithmic differentiation is a technique which uses logarithms and its differentiation rules to simplify certain expressions before actually applying the derivative.The general rule is that the number of initial values needed for an initial-value problem is equal to the order of the differential equation.The Product Rule for Differentiation.Differentiate both sides using implicit differentiation and other derivative rules.Video ansehen20:44Learn the power rule and product rule for derivatives with this calculus video tutorial. We can rewrite this explicit function implicitly as yn = xm.Quotient Rule is used for determining the derivative of a function which is the ratio of two functions. Solve for dy/dx. Some examples of formulas for derivatives are listed as follows: Power Rule: If f (x) = x n, where n is a constant, then the derivative is given by: f‘ (x) = nxn-1. There are a number of simple rules which can be used to allow us to differentiate . For functions whose derivatives we already know, we can use this relationship to find derivatives of inverses without having to use the limit definition of the derivative. More importantly, we will learn how to .
Differentation Rules
That’s any function that can be written: \[f(x)=ax^n\] We’ll see that any function that can be written as a power of \(x\) can be differentiated using the power rule for differentiation. Let y = xm / n, where m and n are integers with no common factors (so m = 2 and n = 5 is fine, but m = 2 and n = 4 is not).Learn all about derivative rules, including product, quotient, chain, sum, and power rules. Between the power rule and the basic definition of the derivative of a constant, a great number of polynomial derivatives can be identified with little effort – often in your head!
Quotient rule
These equations help to relate functions to their derivatives. For instance, if we were given the function defined as: f(x) = x2sin(x) this is the product of two functions, which we typically refer to as u(x) and v(x). The same thing is true for multivariable calculus, but this time we have to deal with more than one form of the chain rule. In the first section of this chapter we saw the definition of the derivative and we computed a couple of derivatives using the definition. And it actually works out to be cos 2 (x) − sin 2 (x) So that is your next step: learn how to use the rules. The derivative of velocity is the rate of change of velocity, which is acceleration. Now apply implicit differentiation.Summary of derivative rules Tables Examples Table of Contents JJ II J I Page8of11 Back Print Version Home Page 25.

Under fairly loose conditions on the function being integrated, differentiation under the integral sign allows one to interchange the order of integration and differentiation.In this chapter, we investigate how the limit definition of the derivative leads to interesting patterns and rules that enable us to find a formula for \ (f‘ (x)\) quickly, without using the limit definition directly. In particular we learn how to differentiate when:Math Cheat Sheet for Derivatives
Differentiation Rules
Basic derivative rules.In single-variable calculus, we found that one of the most useful differentiation rules is the chain rule, which allows us to find the derivative of the composition of two functions. Visit BYJU’S to learn the definition of quotient rule of differentiation, formulas, proof along with examples. The differential equation . As we saw in those examples there was a fair amount of work involved in computing the limits and the functions that we worked with were not terribly complicated. Furthermore, the derivative of a sum of two functions is simply the sum of their derivatives. Replace y with f(x).Example – Combinations.For example, constant factors are pulled out of differentiation operations and sums are split up (sum rule).List of Derivative Rules.
Derivative Calculator • With Steps!
In the next few sections, we’ll get the derivative rules that will let us find formulas for derivatives when our function comes to us as a formula. At this point, by combining the differentiation rules, we may find the derivatives of any polynomial or rational function. Let’s explore how to find the derivative of any polynomial using the power rule and additional properties., are the various rules of differential calculus. This lesson contains plenty of practice problems including examples of c. For example, every fourth derivative of \(\sin x\) equals \(\sin x\), so
Derivative rules
In particular, we will apply the formula for derivatives of inverse functions to . So to continue the example: d/dx[(x+1)^2] 1.
Basic Differentiation Rules For Derivatives
Siyavula’s open Mathematics Grade 12 textbook, chapter 6 on Differential calculus covering 6. If the function is differentiable at , that is if the limit exists, then this limit is called the derivative of at .Differentiation allows us to find rates of change.
Differentiated Instruction: Examples & Classroom Strategies
Derivatives Cheat Sheet
This, and general simplifications, is done by Maxima.

Examples of Derivative Formula.
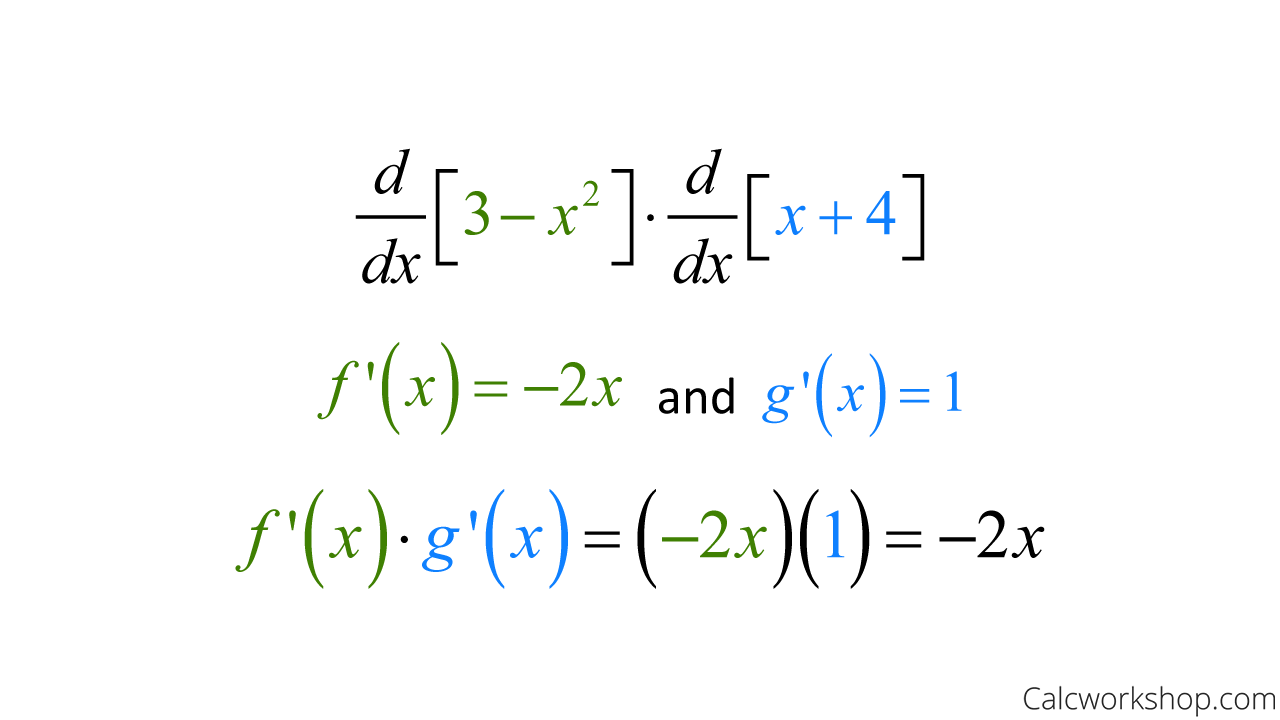
Autor: The Organic Chemistry TutorList of the basic rules of differentiation with examples.
- Die Verschwörung Der Frauen _ Verschwörung (2018)
- Digitales Lernen Wettringen , Lernen digital
- Digital Marketing For Older People
- Die Verschwörung Der Serie _ Die Verschwörer
- Diepholz Berufsschule : Jahnschule Diepholz
- Digitalisierung Der Polizeitätigkeit
- Diktiergerät Für Voice Recorder
- Digitale Proofsysteme _ Alexander Langenhagen
- Diktatur Bedeutung : Autoritarismus
- Dienstleistungsgedanke Personalabteilung
- Diego Ketchup Song – The Ketchup Song (Aserejé) [Chiringuito Club Remix]