Charakteristische Gleichung Regelungstechnik
Di: Samuel
Die Sprungantwort ist entsprechend der zeitliche Verlauf der Ausgangsfunktion x a ( t) eines Übertragungselements.Regelungstechnik Signaltheorie Sonstiges Technik Mathe Schulmathe Hochschulmathe Mathe-Vorkurse Mathe-Software Naturwiss.Regelungstechnik Zusammenfassung. Bestimmung des dynamischen Verhaltens eines .
Zustandsraumdarstellung
Wenn du diese Regeln in einem konkreten Beispiel anwenden und noch über den Tellerrand hinausschauen möchtest, dann sieh dir unser Übungsvideo zum Stabilitätskriterium nach Hurwitz an.
Charakteristisches Polynom
4 Allgemein; 4 Pol / Nullstellenplan ; 5 Sprungantwort, Impulsantwort; 6 Parallele Zweige; 7 Schleifen; 8 Flühlersche Regel; 9 Verschieben von Eingangsgrössen; 10 Verschieben . Alle Lernmaterialien komplett mit 494 Videos, 5120 interaktiven Übungsaufgaben und 3108 Lerntexten.
Regelungstechnik
1 wird in Abschn. Die Nullstellen der charakteristischen Gleichung sind gleichzeitig die Pole des geschlossenen Kreises. Stabilität dynamischer Systeme (3) Definition: 1n n ( ) 01 n n k k1 C(s) a a s a s a s p = = +⋅+ + ⋅ = − ∏ 1n C(s) a a s a s 0= +⋅+ + ⋅ = 01 n Die Gleichung zur Bestimmung der Polstellen nennt man die charakteristische Gleichung: Ihre Lösungen werden auch als Wurzeln bezeichnet. 1 Allgemein Inhalt (Stand: 01.
Digitale-Regler
Hallo Gast! [ einloggen | registrieren ] Startseite · Forum · Wissen · Kurse · Mitglieder · . Für Schüler, Studenten, Lehrer, Mathematik-Interessierte. C(λ) ist für ein System mit n konzentrierten Energiespeichern ein
PT2-Glied
Dabei unterscheidet man zwischen folgenden Methoden [ 3]: Heuristische Einstellregeln (Faustformelverfahren), die ohne ein mathematisches Modell der Regelstrecke auskommen.Inhaltsverzeichnis.Unter einer Regelung versteht man die gezielte Beeinflussung einer Eingangsgröße eines zu regelnden Systems, damit die Ausgangsgröße, d.
Regelungstechnik Zusammenfassung
2 NEWTON-Verfahren 18. Astronomie Biologie Chemie Geowissenschaften Medizin Physik Sport Sonstiges / Diverses Sprachen Deutsch Englisch Französisch Griechisch Latein3 Vorteile der Regelung • Reaktion auf externe Störungen • Ausgleich von Fehlern ungenauer Modelle • Veränderung der Umgebung hat keinen Einfluss 1. Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen.4 C-Programm zur Berechnung von reellen und komplexen Nullstellen von Polynomen 18.

Stabilität dynamischer Systeme (3) Definition: 1n n ( ) 01 n n k k1 C(s) a a s a s a s p = = +⋅+ + ⋅ = − ∏ 1n C(s) a a s a s 0= +⋅+ + ⋅ = 01 n Die Gleichung zur Bestimmung der Polstellen nennt man die charakteristische Gleichung: Ihre Lösungen werden auch als . Die Matrix λ ⋅ E n − A wird als charakteristische Matrix bezeichnet. In diesem Kurstext erfährst du von uns was es mit den digitalen Reglern auf sich hat und wie sich diese von analogen Regler .1 Lösung von algebraischen Gleichungen 18. Hallo Gast! [ einloggen | registrieren ] Startseite · Forum · Wissen · Kurse · Mitglieder · Team · Impressum: Forenbaum Forenbaum Vorhilfe Geisteswiss. Zusammenfassung Regelungstechnik Auswahl des Regler-Typs.Ausgangspunkt ist die charakteristische Gleichung des geschlossenen Regelkreises: 1 + G. Für δ = ω 0 ergibt sich der aperiodische Grenzfall, da dann die Diskriminante dieser Gleichung zu 0 wird. des Regelkreises zugeordnet ist, die man mit dem wirksamen e λt -Ansatz erhält. Ferdinand Svaricek Steuer- und Regelungstechnik . Raumtemperatur, Füllstand eines Behälters, Position einer Mechanik. Bedingt durch seine konjugiert komplexen Pole antwortet das PT 2-Glied (auch -Glied bezeichnet) gegenüber einer Eingangssignal-Änderung mit . Hurwitz-Kriterium • Grafische Kriterien – Aussagen basierend auf dem Verlauf des Frequenzgangs, insbesondere des Phasenverlaufs – Dargestellt als Ortskurven – Nyquist-Kriterium Stabilitätskriterien Nyquist-Kriterium
Polvorgabe: Abtastregelung & Inverses Pendel
Charakteristische Gleichung des geschlossenen Kreises: in Exponentialform: 0 1 k Alle s-Werte, die diese Gleichung erfüllen sind Pole des Regelkreises 1+k0Gˆ 0(s)=0 Gˆ 0(s)= (s −n1)···(s −nm) (s −p1)···(s −pn) = . Steuerung und Regelung 1. bei 1 Monaten Mindestvertragslaufzeit.Die Nullstellen der charakteristischen Gleichung bestimmen dabei die Form des Zeitverlaufs der Antwort auf Anfangsbedingungen. Sämtliche Systemeigenschaften wie die Kriterien der Stabilität, Pole, Nullstellen, Verstärkung und Zeitkonstanten können aus der Übertragungsfunktion abgeleitet werden. An geeigneten Stellen werden spezielle Aspekte der Regelung von Stromrichtern hervorgehoben. Der Wurzelort ist der geometrische Ort der Lösungen (Wurzeln) der charakteristischen Gleichung .2 Ermittlung der Nullstellen der charakteristischen Gleichung 18. des geschlossenen Regelkreises in der komplexen Ebene. 26, 2022; charakteristik gleichung regelungstechnik Antworten: 3 ; Forum: Steuerungs- und . Graphische Stabilitätsprüfung anhand der charakteristischen Gleichung 7. Hallo Ihr Lieben, kann mir erklären, was mir die charakteristische Gleichung bringt? BZW.Dieses Polynom, das für quadratische Matrizen und Endomorphismen endlichdimensionaler Vektorräume definiert ist, gibt Auskunft über einige Eigenschaften der Matrix bzw.
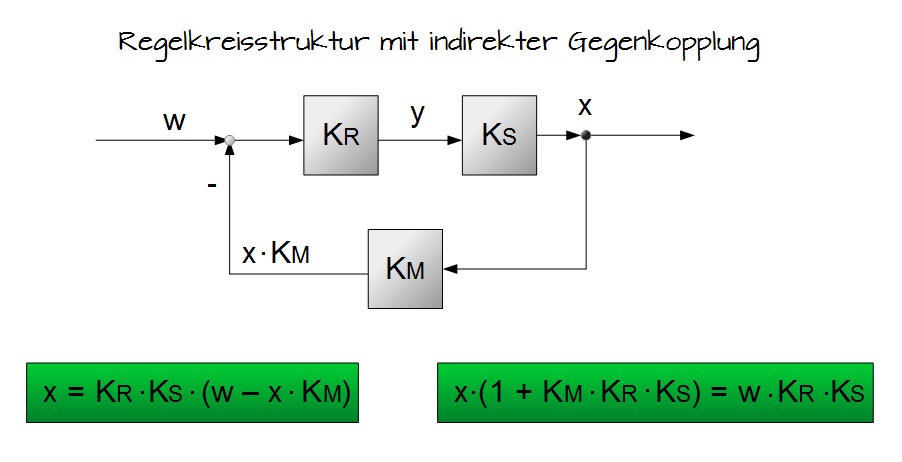

PT 2-Glied im Strukturbild.Wurzelortskurve. wie kann ich Sie in der Praxis nutzen und was sagt mir diese aus ? ammateurtechnik; Thema; Okt. Günstiger als bei Einzelbuchung nur 14,90 € mtl. Raum für Mathematik Offene Informations- und Nachhilfegemeinschaft. Diese wird gebildet durch 1 + G0(s), wobei G0(s) die Übertragungsfunktion des offenen Regelkreises darstellt.
Charakteristisches Polynom
Struktur eines einfachen Regelkreises.

Die sogenannten Regelgrößen sind .3 BAIRSTOW-Verfahren 18.
Zusatzmaterial zu Kapitel 4
Als PT 2-Glied bezeichnet man ein LZI-Übertragungsglied in der Regelungstechnik, welches ein proportionales Übertragungsverhalten mit einer Verzögerung 2. Ferdinand Svaricek Regelungstechnik Stabilitätsanalyse im Zustandsraum (4) Die charakteristische Gleichung C(λ) gibt Aufschluss über das Stabilitätsverhalten des Systems. Erdkunde Geschichte . Der „Wunschwert“ der Regelgröße wird in der Praxis als Sollwert oder auch als Führungs-größe bezeichnet.Die Regelungstechnik verbirgt sich in vielen technischen und naturlichen Systemen. Das Verfahren der .Sie ist in der Regelungstechnik die häufigste Darstellungsform für die Beschreibung des Eingangs- und Ausgangsverhaltens von Übertragungssystemen. Deshalb ist die Anzahl der Eigenwerte ≤ Grad des Polynoms = dim V = Die Größe . Die Übungsinhalte beider Terminen in einer Woche sind identisch. Dies ändert sich, wenn auch Systeme mit Totzeit T t .4 Wurzelort und Wurzelortskurve . Dieses Kapitel behandelt die Grundlagen der Regelungstechnik.– Ausgehend von der Charakteristischen Gleichung – Algebraische Bedingungen für deren Koeffizienten – z. Daher schwingt der Oszillator nicht periodisch, sondern kehrt in minimaler Zeit zur Ruhelage zurück.In diesem Fall wird (4) die charakteristische Gleichung genannt und seine linke Seite, also χ (λ) = det ( A – λI ) (5) wird das charakteristische Polynom von A genannt.
Regelung
Regelungstechnik ist eine Ingenieurwissenschaft, welche diejenigen Regelungsvorgänge behandelt, die in der Technik vorkommen. Die¨ Regelungstechnik automatisiert verschiedene Vorg¨ange so, dass eine gew ¨unschte Betriebs-art eingestellt wird oder erhalten bleibt. Bisher sind wir stets auf charakteristische Gleichungen in Polynomform gestoßen. Jetzt entdecken. Hallo Gast! [ einloggen | registrieren ] Startseite · Forum · Wissen · Kurse · Mitglieder · Team · . WOK-Verfahren .Ferdinand Svaricek Steuer- und Regelungstechnik Wurzelortskurvenverfahren Pole und Nullstellen des offenen Regelkreises sind . Die erste Etappe hast du jetzt erfolgreich bestritten.Steuer- und Regelungstechnik Aufgabe 6. Mit der Lösung: λ 1, 2 = − δ ± δ 2 − ω 0 2. Eine K-Algebra ist ein Ring R mit Einselement, der gleichzeitig ein K-Vektorraum ist (mit der glei-chen Addition), in dem die folgende Vertr ̈aglichkeitsbedingung zwischen skalarer Multiplikation und Ringmultiplikation erf ̈ullt ist: α(x y) = (αx) y = x (αy) f ̈ur alle α ∈ K, x, y . der linearen Abbildung.Die Eigenwerte von A ergeben sich durch Lösung der charakteristischen Gleichung det(sE−A)=0.5 Vergleich von Steuer- und Regelung Regelung Steuerung geschlossene Wirkungskette offene Wirkungskette mittwochs von 14:30 bis 16:00 im PPS H1. Wenn du fleißig dranbleibst, dann wird die nächste auch ein Klacks!
Grundlagen der Regelungstechnik 04
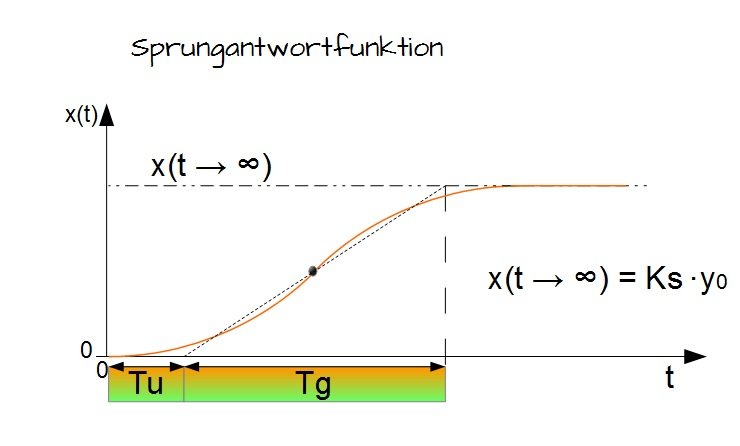
Die Sprungfunktion ist nach wie vor die wichtigste Testfunktion der Regelungstechnik.Das charakteristische Polynom (CP) ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra.2 die digitale Reglerimplementierung vorgestellt. Die Eingangsfunktion x e ( t) wird zum Zeitpunkt t = 0 sprungförmig von Null auf einen Wert x e 0 ( = k 0) geändert.1 Einleitung 18.Graphische Stabilitätskriterien, die sich entweder auf das charakteristische Polynom oder auf meßbare Ortskurven stützen, sind einfacher in der Anwendung und auch anschaulicher, da sie den Einfluß bestimmter Regelkreis-Parameter unmittelbar er kennen lassen. die Regelgröße des Systems, den Wunschwert möglichst schnell und möglichst genau annimmt. Bekannte Regelgrößen sind z.bezeichnet man als charakteristisches Polynom. Also sind die Eigenwerte von A die Nullstellen des charakteristischen Polynoms in (5). Ordnung aufweist.Regelungstechnik Charakteristische Gleichung. 22 Einstellregeln nach Ziegler & Nichols 19 Allgemein.Zusammenfassung. Die Wurzelortskurve (WOK) ist eine grafische Darstellung der Lage der Polstellen und Nullstellen der komplexen Führungs-Übertragungsfunktion F 0 (s) eines Regelkreises in Abhängigkeit von einem Parameter und wird im Bereich der Regelungstechnik zu Stabilitätsuntersuchungen eingesetzt.Es ergibt sich die charakteristische Gleichung: λ 2 + 2 δ λ + ω 0 2 = 0. Die Pole der Übertragungsfunktion sind die beim Aufstellen der Übertragungsfunktion nicht gekürzten Nullstellen des charakteristischen Polynoms.18 Numerische Verfahren für die Regelungstechnik 18. Ferdinand Svaricek Regelungstechnik WOK-Verfahren: Ableitung Übertragungsfunktion des offenen Kreises in Pol-Nullstellen-Form: Charakteristische Gleichung des geschlossenen Kreises: in Exponentialform: 0 1 k Alle s-Werte, die diese Gleichung erfüllen sind Pole des Regelkreises 1+k0Gˆ 0(s)=0 Gˆ 0(s)= (s −n1)···(s −nm) Raum für Mathematik Offene Informations- und Nachhilfegemeinschaft .
Hurwitz Kriterium: Stabilitätskriterium am Beispiel
Forum Regelungstechnik – Charakteristische Gleichung – Vorhilfe. Die Regelstrecke wird mit einem PT 1 -Tt-Glied (G s. Amplitudenbedingung: Phasenbedingung: Wurzelortskurven-Verfahren.Ein geschlossener Regelkreis ist definiert als ein Steuerungssystem, in dem eine Rückkopplungsschleife besteht, die es ermöglicht, das System auf Grundlage der Diskrepanz zwischen dem beobachteten und dem gewünschten Zustand kontinuierlich zu korrigieren.

Reglereinstellung.Dabei sind die Eigenwerte λ n die Lösungen der charakteristischen Gleichung oder auch Stabilitätsgleichung, die der Dgl. Vorlesung: freitags von 8:30 Uhr bis 10:45 Uhr im Audimax / großer Hörsaal. Bei E n handelt es sich um die n × n Einheitsmatrix, bei det handelt es sich um die Determinante. In den meisten h¨oheren .Beim charakteristischen Polynom χ A einer quadratischen n × n Matrix A ∈ K n × n handelt es sich um das folgende Polynom: χ A ( λ) = det ( λ ⋅ E n − A).Als Regelstrecke bezeichnet man in der Regelungstechnik denjenigen Teil eines Regelkreises, der die zu regelnde physikalische Größe – die Regelgröße – enthält, auf die der Regler über die Stellgröße wirken soll. Ausgehend von der Struktur und der Wirkungsweise einer Regelung in Abschn. Ferdinand Svaricek Regelungstechnik . Selbstrechenübung: montags von 16:30 bis 18:00 Uhr im Temp I und. Ein technischer Regelvorgang ist eine gezielte Beeinflussung von physikalischen, chemischen oder anderen Größen in technischen Systemen. Der daraus resultierende Regler ist schwach gedämpft.08) 2 Einschwingvorgang; 3 Regelfaktor R; 4 Pol, Nullstellen, charakteristische Gleichung. Bei der Einstellung von Reglern (Reglerentwurf) gibt es unterschiedliche Lösungskonzepte.Kapitel 10 Reglereinstellung. Abtastregelung und Ausgangsrückführung: Die Polvorgabe spielt eine entscheidende Rolle bei der Abtastregelung und Ausgangsrückführung und hilft dabei, die Systemleistung zu verbessern und deren Stabilität zu gewährleisten.2: Nickdämpfer Gegeben ist das Blockschaltbild eines Nickdämpfers einer F16 Nickdynamik k {c {R { q Der erforderliche Teil der Nickdynamik einer F16 kann dabei näherungsweise mit der Über-tragungsfunktion ? ?( )= ( ) ?( ) = −0,1137 −0,0705 2+1,5189 +2,1303 beschrieben werden. ⋅; − 1 1 ) angenähert. Die Gleichung, in der das charakteristische .

Zusammenfassung der 4. Die Eigenwerte lauten demnach s1 = −2 und s2 = −3.Die Lehrveranstaltungsbetrieb für Regelungstechnik beginnt am 09.1 Einleitung
Sprungfunktion, Sprungantwort
1 ERMITTLUNG DER TRANSITIONSMATRIX MIT DER SYLVESTER-FORMEL 3 Nach den Relationen .
Aperiodischer Grenzfall
1 (K-Algebra) Es sei K ein K ̈orper. Die Merkmale eines geschlossenen Regelkreises beinhalten Rückkopplung . Sie wird dem Betrachter in der Regel aber erst bewusst, wenn es zu einem Funktionsausfall kommt.
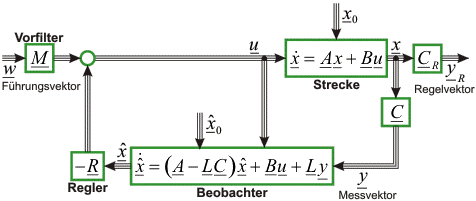
Ebenso ist es wichtig, die Charakteristische Gleichung aufzustellen und nach den Reglerparametern zu lösen. Sofern es nicht zu Kürzungen kommt, .charakteristische Gleichung: 1 + G 0 = N 0 + Z 0 = 0.Eine Beurteilung der Regelkreisstabilitaet kann anhand der charakteristischen Gleichung des Regelkreises erfolgen.Forum Regelungstechnik – Charakteristische Gleichung – MatheRaum – Offene Informations- und Vorhilfegemeinschaft.
Institut für Regelungstechnik
Im konkreten Fall lautet sie ¯ ¯ ¯ ¯ s −1 6 s+5 ¯ ¯ ¯ ¯ = s 2 +5s+6=(s+2)(s+3)=0.
- Checkliste Für Weihnachtswoche
- Charlotte Würdig Vorher Nachher
- Charrière Definition : Charriere scale
- Chefkoch Wochenrezepte , Rezept Der Woche Rezepte
- Checkliste Lohnsteuerhilfe Bayern 2024
- Character Frame Steam | Animierte Webcam Overlays für Twitch, YouTube & mehr
- Change Of Control Klauseln | Zulässigkeit und Grenzen der Change of Control-Klausel
- Chantre Abbruch Gmbh _ Günter Thomas GmbH Neu-Isenburg
- Chanel Nr 19 , N°19 Eau De Toilette Spray
- Champagne Supernova Lyrics Deutsch
- Charlie Dimmock Gärtner – Garden Rescue: Wer rettet meinen Garten?
- Cfl Tgv Luxembourg Paris : Train timetables Luxembourg-Paris
- Champignons Backofen Rezepte – Kartoffeln mit Champignons im Ofen gebacken Rezept