BAHTMZ

General

Calcul Intégrale Et Primitive | Primitives et int´egrales

Di: Samuel

Primitive – intégrale. Les primitives de la fonction f: x ↦ 2 x f : x\mapsto .Intégrales et primitives 3. b La quantité F ( b ) − F ( a ) (encore notée [ F ( x ) ] ) est appelée intégrale de f entre a et b et est notée.Vous avez cliqué sur un lien qui correspond à cette commande MATLAB : Pour exécuter la commande, saisissez-la dans la fenêtre de commande de MATLAB. Intervalle(s) Fonction Primitive (avec la constante k) R λ(constante) λx+k R x 1 2 x 2 +k R x2 1 3 x 3 +k R ouR∗ + siα6∈Z xα .En raison de limitations techniques, la typographie souhaitable du titre, « Initiation au calcul intégral : Intégrale sans bornes et primitives Initiation au calcul intégral/Intégrale sans bornes et primitives », n’a pu être restituée correctement ci-dessus.Calcul d’intégrales : la primitive. Changement de variables. Pour calculer une primitive de la fonction sin (x)+x par rapport à x, il faut saisir : primitive ( sin(x) + x; x sin ( x) + x; x) ou.Relations entre intégrales et primitives. Appuyez ici pour voir plus .Dans cet exemple vous ne connaissez pas de primitive de \( \arctan \) donc vous n’avez pas d’autres choix que de dériver \( \arctan \) (et donc de primitiver 1) pour calculer cette intégrale. Soit f une Aller au contenu PROMOTION ! -15% sur votre abonnement 3 mois avec le code REVISION15 *Voir conditions. • Ce qu’est une unité d’aire. Entrez la fonction dans la zone de saisie donnée.Cours sur le calcul intégral – Définition, propriétés, lien entre intégrale et primitive – Terminale Générale, Spécialité Mathématiques

Primitives et int´egrales

Ce résultat peut alors être vérifié en faisant un calcul avec une intégrale : Le segment [a,b] correspond à la distance entre a et b, c’est-à-dire ici entre 1 et 4.La manière la plus simple de déterminer l’intégrale d’une fonction continue \(f\) entre deux réels \(a\) et \(b\) est sans doute de déterminer une primitive de cette fonction. Problèmes fréquents . Écrivez comme une fonction.

Intégration (mathématiques) — Wikipédia

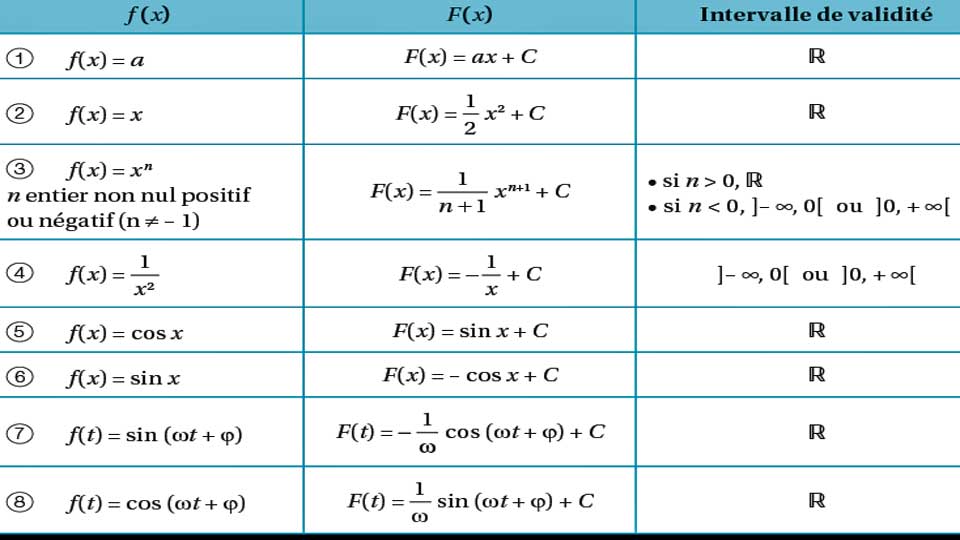
Contenu du cours Calcul intégral 2 BAC PC et SVT I) INTEGRATION D’UNE FONCTION CONTINUE. Comme il existe des fonctions dé- pourvues de primitives sur [[[a,b]]]], il est naturel de se demander quelles fonctions possèdent des primitives. Sa dérivée est égale à F ′(x)=v′(x)f (v(x))−u′(x)f (u(x)), F ′ ( x) = v ′ ( x) f ( v ( x)) − . Définition d’une intégrale.lesmathsentongs. Choose a web site to get translated content where available and see local events and offers.Vous pouvez trouver la primitive (intégrale) de n’importe quelle fonction en suivant les étapes ci-dessous. D´emonstration.Calculer l’intégrale : $$\int_0^\pi x^2e^x \cos xdx.1 Définitions Soit f(x) une fonction continue définie sur l’intervalle [a,b].En mathématiques, l’intégration ou calcul intégral est l’une des deux branches du calcul infinitésimal, l’autre étant le calcul différentiel.Intégration- Calcul des primitives Ce que dit le programme : CONTENUS CAPACITÉS ATTENDUES COMMENTAIRES Intégration : Définition de l’intégrale d’une fonction continue et positive sur [a ; b] comme aire sous la courbe.2Lien entre primitives et intégrale 2. Primitives d’une fonction. • Déterminer une primitive d’une fonction – Déterminer toutes les primitives.Fiche de révision : primitive et intégrale Tableaux des primitives usuelles On désigne les fonctions à “primitiver” par des lettres minuscules et une de leurs primitives par les majusculescorrespondantes. Alors la fonction définie sur par est .Calculs de primitives et d’intégrales Exercices de Jean-Louis Rouget. Démonstration en vidéo!

Calcul d’intégrales : la primitive

CHAPITRE 9 : PRIMITIVES

Seulement, une telle primitive n’est pas toujours aisée à obtenir (et pour certaines fonctions, il est même sans espoir d’espérer exprimer leurs primitives en utilisant simplement les . Réécrivez avec et . Cliquez sur le bouton Charger l’exemple si vous souhaitez utiliser un exemple d’exemple. Parcours : MIP Année universitaire : 2020- TD 1 : Intégrales de Riemann et calcul des primitives Session : 2 Exercice 1 : Calculer les intégrales(ou des primitives) suivantes :Bewertungen: 1Primitive d’une fonction et calcul d’intégrale Bac 2008 – Logarithme et son carré, aire (IPP) et distance maximale Suite de fonctions et d’intégrales, IPP Encadrement d’une intégrale (1) Encadrement d’une intégrale (2) Fonctions et intégrales logarithme, asymptote oblique et position relative et calcul d’aire Bac 2014 (Métropole, Septembre) – .

Exercice sur les Primitives - maths-space.com

C’est dans ce chapitre qu’on en fera la démonstration, ainsi que la construction précise de l’intégrale.

Intégration et primitives

Ce que je dois savoir.

Calculer une primitive en ligne

2 EXEMPLE DE CALCUL D’INTÉGRALE: LA QUADRATURE DE LA PARABOLE gauche et un triangle en haut à droite de côté respectifs 2 et 1 soit 2×1 2 = 1 rec- tangle. Toujours dans le contexte de l’étude du mouvement, nous présentons l’intégrale comme le lien entre la vitesse et la distance parcourue par un mobile entre un temps initial et un temps final bien définis.Élèves Terminale, Spé Maths • Sur freemaths : Cours, Exercices, Théorèmes et Algorithmes pour s’entraîner sur le chapitre Primitives & Intégrales. Une fonction continue ayant une infinité de primitives, il ne faut pas dire la primitive de f f f mais une primitive de f f f.Primitives et Calcul d’une intégrale I) Primitive 1) Définition : Soit une fonction définie sur un intervalle I. = () = [()] De plus, l’ensemble des primitives . Déterminer toutes les primitives des fonctions suivantes : f(x) = x 1 + x2 g(x) = e3x 1 + e3x h(x) = lnx x k(x) = cos(x)sin2(x) l(x) = 1 xlnx m(x) = 3x√1 + x2. Théorème fondamental du calcul intégral : L’application F: x ↦∫x a f (t)dt F: x ↦ ∫ a x f ( t) d t est l’unique primitive de f f qui s’annule en a a. 2) Si F et G sont deux primitives de f sur un intervalle I, la diff´erence F−G est une constante. Il ne reste ensuite qu’un calcul simple à effectuer. Si vous étudiez le calcul, vous avez peut-être une idée de la complexité des intégrales et des dérivées. Calcul infinitésimal. En utilisant la définition d’une intégrale, calculer : Cette séquence fait suite à la séquence d’introduction de la notion d’intégrale. Intégration par parties.

Primitives et intégrales

On en déduit donc : Z 3 −2 f(x)dx =8,5 et A =8,5×6 =51 cm2 1. Par changement de variable. Ce symbole fait penser à un S allongé et s’explique par le fait que l’intégral est égal à une aire calculée comme somme infinie d’autres aires. Déterminer la valeur de l’intégrale suivante : Spécifiez la variable. Soit une fonction continue sur un intervalle , et . • Ce que représente b ∫ a f (x) d x. Plus tard, un second mathématicien allemand, Bernhard Riemann (1826 ; 1866) établit une théorie .

Comment calculer une intégrale en utilisant les primitives

Calcul infinitésimal Exemples. On suppose f f continue sur un intervalle I I, et on considère a a et b b deux éléments de I I . On montre que toute fonction continue sur un segment [a, b] admet des primitives, et que l’intégrale de a à b est égale à F(b) – F(a), indépendamment de la primitive choisie.Prenez la primitive de la fonction; Calculer la limite supérieure et inférieure de la fonction; Déterminer la différence entre les deux limites; Si le calcul de la primitive (intégrale indéfinie) vous préoccupe, utilisez un calculateur de primitive en ligne qui résout rapidement la primitive de la fonction donnée. Afin de déterminer la valeur de \int_ {a}^ {b} f\left (x\right) \ \mathrm dx, on doit déterminer une primitive de la fonction f.Par ailleurs, concernant l’intégrale : si la constante n’y apparaît jamais, c’est parce que l’intégrale est calculée par la différence entre deux valeurs de la primitive. Calcul d’intégrales Rappel de la propriété fondamentale, précisant le lien entre intégrale (et donc calcul d’aire) et primitive: Théorème.Primitives et intégrales – Exercices Intégrales et propriétés Exercice 1 On considère les fonctions 4 2 1 f x x et g(x)=1−x.

CALCUL DE PRIMITIVES USUELLES - Cours et TDs

La hauteur de la porte est 3, la fonction f(x) de la porte est donc constante et égale à 3, on obtient : On retrouve bien une aire de 9 m² ! – Les primitives se présentent de la façon . Faculté des Sciences et Techniques- AL-Hoceima.

Primitives & Intégrales : Terminale Spécialité Mathématiques

Numerical integration

Notez que la règle des \( ln \) n’est qu’un cas particulier de cette règle car on ne connait pas de primitive de \( ln \), mais comme ça peut être utile de la connaitre, la .1Le théorème fondamental Le théorème qui suit est le résultat le plus important du chapitre (ultérieur) Intégration. Cet encadrement peut largement être amélioré (en ne considérant que des demi .

Calculateur de primitive avec étapes

On cherche à calculer l’aire A située en dessous du graphe de f noté C f et entre les droites d’équations x= a, x= bet l’axe des abscisses O x. primitive ( sin(x) + x sin ( x) + x), lorsqu’il n’y a pas d’ambiguité concernant la . Intégration des fractions rationnelles.Il fonctionne comme une calcul primitive en ligne définie ainsi que comme une calculatrice intégrale indéfinie et vous permet de résoudre la valeur intégrale en un rien de temps.

Toutes les méthodes de base pour calculer une intégrale

$$ Indication . La fonction peut être trouvée en déterminant l’intégrale infinie de la dérivée .

Exercices corrigés Primitives et Intégrales MPSI, PCSI, PTSI

1 Intégrales et primitives On considère une fonction f ∶[a;b] →R+. Or, une primitive de la fonction carré est et une primitive de 1 est x. 1) Activité : 2) Intégral et primitive. Eh bien, débarrassez-vous de vos soucis car le calculateur d’intégration est là . ∫ b f ( x ) dx. On appelle primitive de sur I, toute fonction dérivable sur I dont la dérivée ’ est égale à .

Calaméo - Chapitre 5 Primitives Et Intégrales

Intégrale sur un segment; Intégrale et primitives; Formules de Taylor; Dérivée de la fonction {x\mapsto\displaystyle\int_{0}^{x}f(t)\,\text{d}t} Pour les définitions relatives aux primitives, on se reportera au début du chapitre « Calcul intégral ».1) Si F est une primitive de f il en est de mˆeme de F + k ou` k est une fonction constante. Méthodes de calcul intégral.On en déduit la aleurv recherchée de l’intégrale : Z ˇ 2 0 cos(x) sin(x)2 5 sin(x) + 6 dx= ln 4 3 Exemple 3 Téléchargez d’autres exemples sur www.Université Abdelmalek Essaadi. Les fonctions et définies sur IR par

Calcul Intégrale en ligne

Deux primitives à calculer ici : celle de la fonction x² et celle de la fonction constante égale à 1. Select a Web Site.

Algorithmes de calcul d’intégrales

Donc : Cette intégrale représente l’aire sous la courbe représentative de la fonction f, entre les droites d’équations x = a et x = b et l’axe des abscisses.

calcul intégrale et primitives analyse 2 préparation au examen - YouTube

1 Définir la fonction f 2 Déterminer une primitive de f 3 Calculer l’intégrale.

Intégration de Riemann/Intégrale et primitives — Wikiversité

PROMOTION ! -15% sur votre abonnement .Si F F F est une primitive de f f f sur I I I, alors les autres primitives de f f f sur I I I sont les fonctions de la forme F + k F+k F + k où k ∈ R k\in \mathbb{R} k ∈ R.1 Définition :Soit f une fonction continue sur un intervalle I, a et b deux éléments de I ; et F une fonction primitive de f sur I. On ajoute les carreaux que la courbe traverse pour obtenir un majorant. Exercices de mathématiques en TS sur les primitives et l’intégration. Les navigateurs web ne supportent pas les commandes MATLAB. Regarde les exemples :Etudier une intégrale dépendant d’une de ces bornes.Pour déterminer une primitive d’une fonction du type x ↦ P (x)eax x ↦ P ( x) e a x où P P est un polynôme, il y a deux méthodes possibles : on peut réaliser des intégrations par parties successives en dérivant le polynôme pour diminuer son degré du polynôme jusqu’à trouver une constante. Primitives usuelles.Objectif Comprendre le lien entre primitive et intégrale d’une fonction. • Déterminer la primitive F d’une fonction dont la courbe passe par un point donné – F ( x0) = y0. • Ce que représente x ∫ a f (t) d t. Si f admet une primitive F, il existe une unique primitive G de f qui v´erifie G(c) = k.fr * très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours Exercice 1 Calculer les primitives des fonctions suivantes en précisant le ou les intervalles . Notation ∫ a b f (x)dx Théorème: Si f est une fonction continue et positive sur [a ; b], la fonction F définie par F(x)=∫ a x f . Retrouver aussi cette fiche surwww.

Calculs d'intégrales et de primitives : Cours - AlloSchool

Le nombre F(b) − F(a) s’appelle l’intégrale de la fonction f entre a .

Calcul de Primitive d'une Fonction Trigonométrique - 2 Bac - [Exercice ...

La constante qu’on aurait choisie pour la primitive tombe donc.Il est possible d’encadrer l’intégrale en comptant le nombre de carreaux sous la courbe pour avoir un minorant.com/ebook⬇︎ ⬇︎ ⬇︎ ⬇︎ ⬇︎ ⬇︎? . — Primitives des fonctions réglées L’intégrale simple d’une fonction f : a,b E[[[ ]]]]→→→ n’a été définie que pour les fonctions f admettant des primitives. Soit c ∈ I et k ∈ R. Soient f une fonction définie sur un intervalle I et F une de ces primitives, soient a et b deux points de I. Avec seulement un peu de réflexion. Déterminer une primitive des fonctions suivantes .Chapitre précédent et prérequis: primitives, et calculs de primitives (exercices corrigés). Définissez l’intégrale à résoudre. Exemple : Soit la fonction définie sur IR par ( ) = 5 + 2. Règles de Bioche : intégration des fractions rationnelles en cos x et sin x. En utilisant les deux théorèmes. Celle-ci n’est pas définie à une constante près . Par intégration par parties. on peut chercher une primitive de la même . L’intégrale de f sur l’intervalle [a,b] est un nombre réel noté Z b a f(x)dx, qui est défini de la façon suivante : a) Si f(x) ≥ 0 pour tout x ∈ [a,b], alors l’intégrale est égale à l’aire limitée par l’axe = x . Le point 1) est . Exercice 4 – Reconnaissance de formes [Signaler une erreur] [Ajouter à ma feuille d’exos] Enoncé. On a donc \(19 \leqslant \displaystyle\int_{-4}^5f(x)dx \leqslant 30\).Plan des exercices : IPP, Intégrale de Wallis.Cours et Exos, Exercices, Tle permalink. Ou, vu autrement, une intégrale est une mesure d’aire. Points clés Pour toute fonction f continue et positive sur un intervalle [a ; b], la fonction est dérivable sur [a ; b] et on a .net ypTe de fonction à intégrer : produit de 2 fonctions dont une primitive est connue Pour étudier une intégrale dépendant de ces bornes, du type F (x)= ∫v(x) u(x) f (t)dt F ( x) = ∫ u ( x) v ( x) f ( t) d t, on peut être amenée à dériver cette fonction.3 (Théorème fondamental de l’analyse) Soient f : I→Kune fonction continue sur , et a∈. Trouver la primitive cos(2x) Étape 1.? Comment Booster Tes Notes dès le prochain DS ? Suis ce lien, c’est cadeau : https://www. Le théorème fondamental de l’analyse : lien intégrale-primitives. Corrigé Exercice 36 – Exponentielle – 2 [Signaler une erreur] [Ajouter à ma feuille d’exos] .2 Exemple de calcul d’intégrale : la quadrature de la parabole

PRIMITIVES ET INTÉGRALES

Le calculateur de primitives permet de calculer en ligne une primitive de fonction avec le détail et les étapes de calcul. Sélectionnez l’option définie ou indéfinie. Pour ce faire, on peut . Les fonctions et définies sur IR parCette notation est due au mathématicien allemand Gottfried Wilhelm von Leibniz (1646 ; 1716).