Bipartite Graph Problems | On the Partial Vertex Cover Problem in Bipartite Graphs

Di: Samuel

extremal problems, because Tura´n’s theorem and his questions were the most important roots of this huge area [242], [243]. Generally, we have a Universe of graphs, U, where this universe may be the family of ordinary graphs, or digraphs, or hypergraphs, or ordered graphs, or bipartite graphs, etc and a property P, saying, e. Whether it’s .Constrained Matching Problems in Bipartite Graphs. The anti-Ramsey number is the maximum number of colors in an edge-coloring of G with no rainbow copy of H. Eigenvalue-extremal problems6: maximize the maximum eigenvalue λ(Gn) under the condition that Gn does not contain .An edge colored graph is called rainbow if all the colors on the edges are distinct.

Some Matching Problems for Bipartite Graphs

On one hand we give an introduction to this field and also describe many important results, methods, problems, and constructions.1 (A matrix and its representing graph) A = 1 1 1 1 0 0 0 1 1Originally a complete graph was considered as G. One area of application for which the study of crossing number is useful is graph visualization where lowering of the number of the edge crossings can improve the readability of the resulting layout.The format of the answer depends on whether the graph is bipartite or not.What is and how to solve the unweighted bipartite graph matching problemSupport me by purchasing the full graph theory course on Udemy which includes additio. A bipartite graph that doesn’t have a matching might still have a partial matching. The final section will demonstrate how to use bipartite graphs to solve problems. In this paper we study the parameterized complexity of the bipartite permutation vertex deletion . If the graph is bipartite, print two lines.

Matching in Bipartite Graphs

Hence, we can use maximum bipartite matching algorithms to solve the minimum vertex cover problem in polynomial time for bipartite graphs. We discuss their applications and show the strong NP-hardness of both problems. Your task is to complete the function isBipartite () which takes V denoting no.A subgraph H of an edge-colored graph G is rainbow if all of its edges have different colors., that G∈ U

Complete Bipartite Graph

Bipartite graphs, also known as two-mode networks, are a fascinating and fundamental concept in graph theory that serve as the backbone for many complex optimization problems. cool problem chawlajay111: 2021-12-31 05:29:17. This problem is also called the assignment problem. Understanding the. A set of problems which has attracted considerable interest recently is the set of node-deletion problems.Bipartite Graphs and Problem Solving Jimmy Salvatore University of Chicago August 8, 2007 Abstract This paper will begin with a brief introduction to the theory of graphs and will focus primarily on the properties of bipartite graphs. Munaro On line graphs of subcubic triangle-free graphs Discrete Math., directly solving the primal problem not approximately solving.

Problem

If any of the adjacent vertices are of the same color, the graph is not bipartite. 1: Distance between Vertices. Kuhn based on the ideas of two hungarian mathematicians (Dénes Kőnig and Jenő Egerváry). Expected Time Complexity: O (V + E) P(i,j)∈M cij.

Is Graph Bipartite?

A set $C \subseteq V$ is called a k-path vertex cover of G, if each k-path in G contains at least one vertex from C. 1 Graphs A Graph G is defined to be an .they all describe the same problem.Step 1: Verify the given transportation problem is balanced or unbalance. The idea is very simple.In this paper, we consider a complete bipartite graph as the host graph and discuss some .Those properties for which the bipartite restriction of the node-deletion problem is polynomial and those for which it remains NP-complete are characterized.

bipartite graph

The so described graph is bipartite because there are per deﬁnition no edges within V1 or within V2.

On the Partial Vertex Cover Problem in Bipartite Graphs

Generalized Turán Problems for Complete Bipartite Graphs

• Finding a maximum weight matching in bipartite graphs in time $O(n\sqrt{m}N\log^{2}n)$, where N is the largest edge weight.

The bipartite graph in the figure below has vertices | Chegg.com

A2: Bipartite Graphs find applications in various domains, such as social network analysis, scheduling problems, and matching theory. A bipartite permutation graph is a permutation graph which is bipartite. In this paper we characterize those properties for which the bipartite restriction of the node-deletion problem is polynomial and those for which it remains NP-complete.

Bipartiter Graph » Definition, Erklärung & Beispiele Übungsfragen

In a separate work we have presented an algorithm for .

Bipartite Graph

Median problems which will be called here Loebl–Koml´os–S´os type problems: GivenagraphGn,whichmanddensurethatifGn hasat leastmverticesofdegree≥d,thennGcontainssomeL∈L. Ein Graph mit mindestens zwei Ecken ist bipartit, wenn er keinen Kreis mit ungerader Anzahl an Kanten enthält. Many researchers have also studied some other variations of these problems, see [ 1, 3, 4, 5 ]. To separate the vertices of the graph in two sets such that no two vertices of a set are connected, we will try to color the vertices of the graph using two colors only. Proof of a conjecture on cycles in a bipartite graph.Dominating induced matching in some subclasses of bipartite graphs. J Graph Theory, 31: 333–343 (1999) Article MATH MathSciNet Google Scholar Wang H.

The bipartite graph. | Download Scientific Diagram

The anti-Ramsey problem is to decide the maximum number of colors in the edge coloring . The decision version of the MEB problem is NP-complete for general graphs [ 1] and it also remains NP-complete for bipartite graphs [ 2 ].Network flow problem example: The Elementary Math problem!Support me by purchasing the full graph theory course on Udemy which includes additional problems, .

Bottleneck subset-type restricted matching problems

, a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent) such that every pair of graph vertices in the two sets are adjacent. The most common example of a two-colored graph is a bipartite graph, in which each edge connects two nodes of opposite colors. A matching M in a graph G = ( V , E ) is . of vertices and adj denoting adjacency list of the graph and returns a boolean value true if the graph is bipartite otherwise returns false. We show that one problem cannot be approximated in polynomial time within a factor of .Graph Combin, 16: 359–366 (2000) Article MATH Google Scholar Wang H. The general node-deletion problem can be stated as follows: Given a graph, . A rainbow copy of a graph H in an edge-colored graph G is a subgraph of G isomorphic to H such that the coloring restricted to the subgraph is a rainbow coloring. Remarkably, the converse is true. On 2-factors of a bipartite graph. There is a slight problem here: we shall L also consider the case when not only some L is bipartite but χ(Gn)=2 is as well.In this paper, we examine variants of the partial vertex cover problem from the perspective of parameterized algorithms. This will consist of two sets of vertices A and B with some edges connecting some vertices of A to some vertices in B (but of course, no edges between two vertices both in A or both in B ). Else, it is bipartite. For graphs H, F and integer n, the generalized Turán number ex ( n , H , F) denotes the maximum number of copies of H that an F -free n -vertex graph can have. The deﬁnition also describes a unique graph for every matrix-structure except for permutation. We study this parameter when both H and F are complete bipartite graphs. Bipartite Graphen haben verschiedene Eigenschaften:. Return true if and only if it is bipartite. IDSIA Manno-Lugano, Switzerland. A matching of A is a subset of the edges for which each vertex of A belongs to exactly one edge of the subset, and no .The problem of the crossing number in graphs has been studied for decades [8, 7, 5, 2].

Maximum Weighted Edge Biclique Problem on Bipartite Graphs

Later, the algorithm was improved by James Munkres. The problem can be solved using the Hungarian Method that was developed in 1955 by Harold W.

The complete bipartite graph K 2 ,2' | Download Scientific Diagram

A permutation graph can be defined as an intersection graph of segments whose endpoints lie on two parallel lines $$\\ell _1$$ ℓ 1 and $$\\ell _2$$ ℓ 2 , one on each. Practice Problems¶ Kattis – Gopher II; Kattis – .In this article, we first adopt the bipartite graph strategy to reduce the time complexity of SC, and then an improved coordinate descent (CD) method is proposed to solve the primal problem directly without singular value decomposition (SVD) and postprocessing, i. This is the case when contains some bipartite graphs.Abstract and Figures. We need one new definition: Definition 5.

What is Bipartite Graph with Example?

; Die Mengen A und B eines bipartiten Graphen sind sogenannte stabile . If the algorithm will find a smaller matching, then since it is maximum weight, there is no matching of weight k. Step 2: If the problem is unbalanced transportation problem by introducing dummy row(s) or dummy column(s) with zero transportation cost.

Bipartite Graph - Scaler Topics

Similar problems (but more complicated) can be defined on non-bipartite graphs.

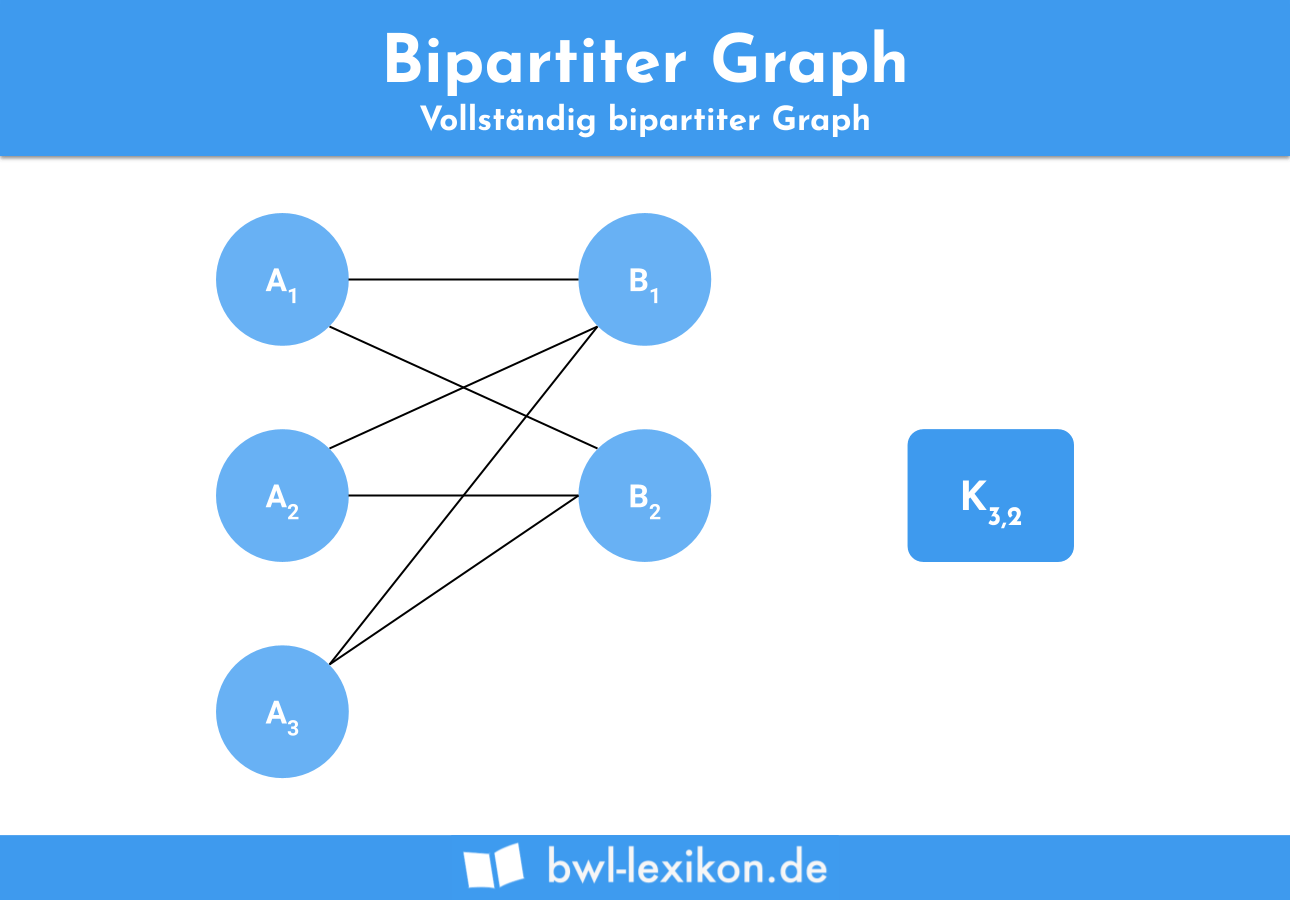
The History of Degenerate (Bipartite) Extremal Graph Problems.; Ein vollständiger Graph hat genau m + n Ecken und m*n Kanten. The projection of this bipartite graph onto the alphabet node set is a graph that is constructed such that it only contains the alphabet nodes, and edges join the alphabet nodes because they share a connection to a . Every bipartite graph (with at least one edge) has a partial matching, so we can look for the largest partial matching in a graph.

Solved Draw the complete bipartite graph K_2,5. How many | Chegg.com

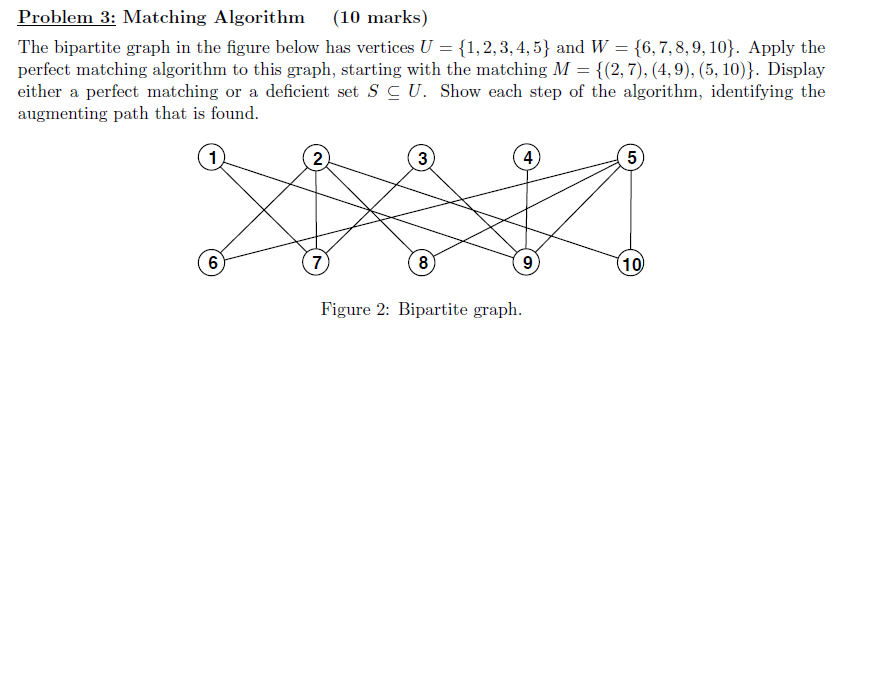
Folgende Situation wird dabei betrachtet: Gegeben sei eine Menge von Dingen und zu diesen Dingen Informationen darüber, welche davon einander zugeordnet . {monaldo,[email protected] don’t need to read or print anything.Suppose you have a bipartite graph G.As shown in the figure above, we start first with a bipartite graph with two node sets, the alphabet set and the numeric set. 1965) or complete bigraph, is a bipartite graph (i. Step 3: Draw the graph of the transportation problem dependent on the situation of the supplies and demands for the graphical .

On Enomoto’s problems in a bipartite graph

We study the following generalization of maximum match-ings in bipartite graphs: given a bipartite graph such that each edge has a unique color cj, we are asked to find a . Explanation: There is no way to partition the nodes into two . ayush_7901: 2022-07-28 14:49:57.In the k-path vertex cover problem, we are given a graph G and asked to find a k-path vertex cover of minimum cardinality.The Maximum Edge Biclique (MEB) problem is to find a biclique in G with maximum number of edges.This problem is so much recommended for those who want to learn about bipartite graphs. Recall that in the classical vertex cover problem (VC), we are given a graph $$\\mathbf{G = \\langle V, E \\rangle }$$ G = V , E and a number k and asked if we can cover all of the edges in $$\\textbf{E}$$ E , using at . J Graph Theory, 31: 101–106 (1999) In the above focus problem, the goal is to assign each node (friend) of the graph to one of two colors . An edge e ∈ E is said to dominate itself and all other edges adjacent to it.However, Kőnig’s theorem gives that, for bipartite graphs, the cardinality of the maximum matching equals the cardinality of the minimum vertex cover.Understanding the fundamentals of bipartite graphs opens the door to a wide range of optimization and problem-solving techniques that are applicable in real-world scenarios. Second line should contain s .Graph two-coloring refers to assigning a boolean value to each node of the graph, dictated by the edge configuration. The importance of the Degenerate . The first should contain the letter Y (short for YES ) followed by a space, and then a single integer s s ( 0 ≤ s ≤ n 0 ≤ s ≤ n ) — the number of vertices in one of the partitions. For ordinary graphs (r = 2) we often call the degenerate extremal graph problems bipartite extremal problems. The distance between vertices v v and w w, d(v, w) d ( v, w), is the length .Eigenschaften bipartiter Graphen. On one hand we give an introduction to this .An NP-hard problem in bipartite graphs SIGACT News 7 26-26 (1976) NP-complete on bipartite ∩ cubic ∩ planar A.

LNCS 7422

Finding a maximum matching in general graphs in time $O(n\sqrt{m}\log^{2}n)$. The Hungarian Method.6 1210-1226 (2017) NP-complete on bipartite ∩ girth >=9 .We introduce two problems related to finding in a weighted complete bipartite graph a special matching such that the maximum weight of its some subsets is minimal.Given an instance of subset sum, create the graph, use the algorithm A, find the maximum weight matching not exceeding the constraints, and answer yes iff the maximum matching found by the algorithm has weight exactly k. Example 1: Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]] Output: false.Since the node cover problem becomes polynomial on bipartite graphs, it might be hoped that this is the case with other node-deletion problems too.A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.By this we mean a set of edges for which no vertex belongs to more than one edge (but possibly belongs to none).For $k=3$, the problem becomes the well-known 3-path vertex . In social networks, for instance, they can model relationships between different types . A subset M ⊆ E of edges of a graph G = ( V , E ) is called a matching if no two edges of M share a common vertex.Let $G=(V,E)$ be a simple graph.Minimum weight perfect matching problem: Given a cost cij a perfect matching of minimum cost where the cost of a matching for all (i, j) E, find. This paper is a survey on Extremal Graph Theory, primarily focusing on the case when one of the excluded graphs is bipartite. Do check for all components (4 WA because of this) .A complete bipartite graph, sometimes also called a complete bicolored graph (Erdős et al.The goal is to find a perfect matching that minimizes the sum of edge weights.Matching (Graphentheorie) Die Theorie um das Finden von Matchings in Graphen ist in der diskreten Mathematik ein umfangreiches Teilgebiet, das in die Graphentheorie eingeordnet wird. This will be illustrated with an example. Our quantum algorithms are faster than the best known classical deterministic algorithms for the corresponding . Monaldo Mastrolilli and Georgios Stamoulis.It is easy to see that all closed walks in a bipartite graph must have even length, since the vertices along the walk must alternate between the two parts. is given by c(M) =.

BAHTMZ

General